指数型阻尼模型复模态更新及阻尼矩阵识别
汪梦甫,肖诗颖
(湖南大学土木工程学院,湖南长沙 410082)
实际工程中振动的发生通常不可避免,因此研究者们广泛关注于如何通过结构耗能(即阻尼)来进行结构减振.但阻尼不能直接测量得到,而是根据假设的阻尼模型在宏观上近似地表达,因此对阻尼模型的假设很大程度上影响着结构动力分析的准确性和可靠性[1].由于经典粘滞阻尼模型自身存在不足,为了满足工程界日益复杂的工程材料和结构的需要,研究者们近年来提出了一些新的阻尼模型,最早由Biot[2]提出的卷积型非粘滞阻尼模型就是其中的一种.该模型假设阻尼力不仅依赖于瞬时速度,而且与速度的时间历程相关,数学表述为质点速度与核函数的卷积[3].在Woodhouse、Adhikari等人[4-5]的进一步发展下,卷积型非粘滞阻尼模型多年来得到了不同领域动力分析的研究和应用.其中,作为卷积型阻尼模型的一个特例,指数阻尼模型在数学计算上较为简单,且能够更加合理地表述阻尼的物理本质,因此本文选择对指数阻尼模型进行研究.
结构系统的参数识别作为现代结构动力学问题的反问题之一,可以根据模态试验并结合理论分析来处理实际工程中的振动问题[6-8].然而此过程中,对阻尼矩阵的预估是难点,并且通常结构阻尼值由经验确定,并假定结构各阶模态阻尼比相同,这与实际情况不符[8],因此有必要对结构阻尼的识别进行研究.但目前的阻尼识别方法一般针对粘滞阻尼模型,对非粘滞阻尼模型阻尼识别的研究较少,国内外主要有如下研究:Adhikari等[9]根据一阶摄动法,率先将复模态分析法扩展到了指数型非粘滞阻尼模型的识别中去,然而该方法对模态参数识别的精度要求较高,且识别阻尼矩阵需要用到全模态;潘玉华[10]在Rayleigh阻尼模型的基础上,提出了指数型比例阻尼模型,假设指数阻尼核函数的阻尼系数矩阵具有和Rayleigh阻尼相对应的形式,并给出了相应松弛因子的迭代计算方法;王禹[11]将阻尼矩阵分解法拓展到指数型非粘滞阻尼模型中,识别该模型的阻尼系数矩阵,该方法能够在只获得低阶模态信息的情况下较为准确地识别出阻尼系数矩阵.
在结构参数识别过程中,通常需要依据一部分有限元模型分析值来识别所需要的真实值,但往往有限元理论分析结果与试验测量结果存在差异,因此可以依据试验结果对分析模型进行更新,使得更新后的模型能更加精确地反应结构的动力响应[12],从而提高结构参数识别的准确性.
基于以上研究背景,本文研究了在模态测试的基础上对指数型阻尼模型中进行阻尼系数矩阵识别及复模态更新的方法,并在此基础上提出了新的松弛因子识别公式.
1 指数型阻尼系统阻尼系数矩阵识别
1.1 阻尼系数矩阵识别
考虑只含有一个阻尼核函数的N自由度线性系统动力微分方程为[3]:

式中:x(t)∈RN;MT、KT∈RN×N分别为系统真实的质量和刚度矩阵.本文使用的指数型非粘滞阻尼模型的阻尼核函数为GT(t)=CTe-μt,其中CT∈RN×N为阻尼真实系数矩阵,则动力微分方程(1)可写为:
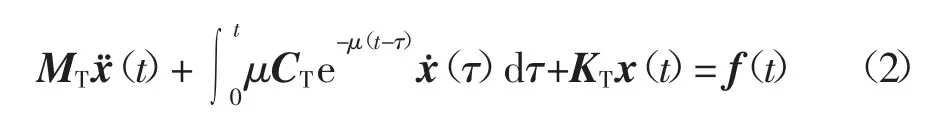
假设对系统进行有限元分析时采用的质量、刚度和阻尼系数矩阵分别为MA、KA和CA,则该有限元分析系统动力方程可写成:
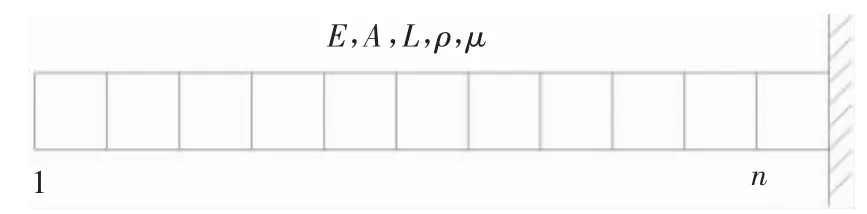
通常有MT≠MA,CT≠CA且KT≠KA.对系统进行模态振动测试可获得m 对式(1)进行拉普拉斯变换可得[5]: 式中:sj和zj分别表示系统第j阶特征值和特征向量.将方程(4)改写成矩阵形式为: 式中:WC是n阶对称正定的加权矩阵,I为n阶单位矩阵.记Z=ZR+iZ1,S=SR+iS1,代入方程(5),令实、虚部分别等于零可得: 其中, 方程(7)(8)可组合为: 其中,A=[AR,AI],ψ=[ψR,ψI].于是最优化问题(6)可写成: 按文献[12]提出的借助于拉格朗日乘子法与矩阵奇异值分解修正粘滞阻尼矩阵的方法,本文优化问题(14)可构建出如下拉格朗日函数: 将函数f分别对LC和ψ 求偏导,并分别等于零,可得: 设LC为非奇异矩阵,则方程(16)可以写为: 方程(18)关于λ 有解的充分必要条件为[12]: 化简后可得: 若取分析阻尼矩阵CA=0,则: 与粘滞阻尼系统类似,从文献[13-14]可知,修正的阻尼系数矩阵一般依赖于加权矩阵WC,令特征方程残量E为: 式中:ej(j=1,…,N)是N ×m阶矩阵E的第j个行向量. 如果E=0,则CT=CA,E中元素的大小在一定程度上反映了CA与CT之间误差的大小[13].可以用矩阵E第j行的范数||ej||来衡量该系统相应第j自由度下识别的误差值,为此选择WC为对角矩阵,为较小的||ej||所对应的WC中的第j个元素分配数值1,较大的||ej||所对应的WC中的元素则分配一个较大的标量[14]. 文献[15]中研究了非粘滞阻尼模型识别问题,提到由于复模态虚部的量级比相应的实部要小得多,更易受实验噪声的影响,并通过梁试验进一步说明了该问题.文献[14]中研究了非比例阻尼模型识别和模态更新,也提到了复模态虚部值的问题.由上述研究可知,由于试验误差及噪声的影响,模态测试所得到的振型一般不满足特征方程(4),从而在阻尼矩阵识别时,可以对复模态虚部进行更新,提高阻尼系数矩阵识别的准确性. 按文献[15]提出的特征向量正则化方法,对方程(4)左乘,可以得到: 对方程(4)取第k阶,转置后,再右乘zj,所得方程与方程(17)相减后可得: 将方程(31)两边除以(sj-sk),j≠k,可得: 设δs=sj-sk,式(32)可写成: 当sk→sk时,δs→0,对方程(33)取极限,从而有: 将G(s)=μ/(μ+s)C代入式(34),可得: 其中,θk为非零常数,对θk的定义可见文献[15]相关描述,对θk的不同选择对应着特征向量的不同正则化条件. 在阻尼很小的情况下,系统复特征向量的实部近似等于无阻尼情形下的相应振型,复特征值的虚部近似等于无阻尼系统的频率[15].因此定义阻尼系数矩阵C为一阶小量(记为o(α)),K和M为数量级l(记为o(l)),其中α< 忽略高阶小项o(α2),因此式(38)可写为: 由于模态测量误差对振型虚部影响更大,则对复模态的修正主要是对振型虚部修正,则问题转化为已知质量矩阵M、刚度矩阵K、复特征值sk及复特征向量实部zkR,求能满足特征方程(37)的复特征向量虚部zkI.将方程(37)中的sk、zk和θk按实部和虚部展开,并将式(43)代入方程(37)消去刚度矩阵K,舍去方程中的o(α2)及更高阶小量,可得: 将方程(44)按实部和虚部分别拆分为如下两个方程: 联立方程(45)(46)可以解出: 代入方程(45)(46)中,可以得到同一个解: 式(49)的基本解为[14]: 式中:β∈R(N-1)×1为任意矩阵,V∈RN×(N-1)满足如下条件: 在模态虚部的试验测量值误差较大的情况下,若是只需要利用zkI识别得到阻尼系数矩阵,则可以令β=0,于是复振型虚部更新值为: 由于目前对松弛因子的识别研究较少,本文提出了新的松弛因子识别过程.记第k阶模态有,zk=zkR+izkI,sk=skR+iskI,代入方程(4),令实、虚部分别等于零可得: 其中: 将式(55)~(58)依次代入式(61),化简后有: 约去方程中的o(α2)及更高阶小量,化简后可得指数阻尼模型松弛因子的表达式为: 从式(63)中可以看出,由于m个不同的模态阶可以得到m个μ 的值,如果选择不同的k得到的μk相差不大,则可以认为该阻尼系统只有一个松弛因子μ;如果得到的μk差异很大,则说明系统存在多个松弛因子,需要对该指数阻尼模型进行扩充.在μk相差不大的情况下,μ 值有以下3种取法: 1)任意选取第k阶模态参数来识别松弛因子μ,例如取k=j ≤m,则有: 2)对不同阶模态参数识别得到的μk取平均值来获得松弛因子μ,则有: 3)对分子和分母分别进行求和,并以其比值获得松弛因子μ,则有: 为了验证本文提出的阻尼识别方法的适用性和有效性,利用文献[11]中的7自由度系统进行模拟计算.该系统质量矩阵、刚度矩阵和阻尼系数矩阵真实值分别为: 该体系的自由振动方程为: 其中,μ 为松弛因子.假定分析阻尼系数矩阵CA=0,权矩阵取为WC=diag(1 1 1 1 1 1 1),运用式(28)识别指数型阻尼系数矩阵C.松弛因子μ 可被表示为[16]: 式中:Tmin表示最高阶无阻尼固有频率所对应的周期,这样结构的阻尼机制可以由γ 的取值来控制,γ越小,阻尼机制就越接近于粘滞阻尼[16].下面分别取γ=0.002、0.2、2三种情况识别阻尼系数矩阵,具体阻尼系数识别值见表1,表1中仅给出了阻尼系数矩阵对角线上的值的大小. 从表1中可看出,本文提出的方法能较好地识别出阻尼系数矩阵,但随着γ 的增大,系统的非粘滞阻尼特性逐渐增强时,想要精确识别出阻尼系数矩阵所需要的模态数目逐渐增加;当γ 增加到2时,需要取得全模态才能精确识别出阻尼系数矩阵. 当γ 取值较大时,对阻尼系数矩阵识别误差较大且所需模态数较多的原因,认为和文中识别公式(28)中的广义逆矩阵有关.通过MATLAB多次计算可以发现,当γ 值增大,矩阵ψ 的条件数也逐渐增大,求广义逆矩阵时精度难以提高,从而误差变大.γ 值一定时,随着选取的模态阶数增加,矩阵ψ的条件数减小,从而精度越高. 表1 阻尼系数矩阵对角线上数值的识别值Tab.1 Identification values of the damping coefficient matrix diagonal values 按文献[11]的识别方法对阻尼系数矩阵进行识别的结果见表2.表2中给出的是能较为精确地得到阻尼系数矩阵所需的最小模态阶数,以及在该模态阶数下的阻尼矩阵识别情况.将表1与表2的结果进行比较,可以看出,在不同的取值以及不同的模态阶数下,文献[11]方法的识别精度均要高于本文的识别方法. 表2 按文献[11]识别得到的阻尼系数矩阵对角线上数值Tab.2 The diagonal values of damping coefficient matrix identified by reference[11] 取文献[17]中含指数阻尼的轴向振动悬臂杆模型作为算例,分析两种方法在对不同自由度下阻尼矩阵进行识别的耗时情况.该悬臂杆模型如图1所示. 图1 轴向振动悬臂杆模型Fig.1 Axially vibrating free-fixed rod 该悬臂杆单元质量矩阵和单元刚度矩阵分别为: 本文中该悬臂杆参数取为:ρ=7.8×103kg/m3为杆件密度;A=6.25 × 10-4m2为杆件截面面积;E=2.1×1011N/m3为弹性模量;L=4 m为杆长;Le=L/n为每个杆单元的长度;n为悬臂杆划分的单元数目.系统的阻尼系数矩阵设为C=α0M+α1K,其中系数α0和α1取为: 式中:阻尼比ξ 取0.05,第j阶无阻尼固有频率为ωj松弛因子μ 按式(67)计算,其中γ取为1. 分别取n=10、20、40和80四种情况,按本文提出的方法和文献[11]的识别方法取全模态识别阻尼系数矩阵C所需要的时间见表3.从表3中可以看出,由于文献[11]的识别过程涉及了大量的循环运算,若结构的自由度数较多,在利用MATLAB进行求解时会耗时较长;在本文的方法中,结构的自由度取值对运算时间影响相对而言不大.因此,在自由度较少的情况下,利用文献[11]提出的阻尼系数矩阵识别方法可以得到更好的结果;在结构自由度数较多时,如果有运算时间上的需求,采用本文提出的方法则更有效率. 表3 不同n值时识别阻尼系数矩阵所需的时间Tab.3 The time needed to identify the damping coefficient matrix with different n values 取案例1中的7自由度系统作为算例进行分析,取γ=0.02.现给复模态虚部添加均值为0、标准差为0.1%的噪声,复模态实部取为精确值,更新前阻尼矩阵的识别情况见表4.从表4中可以发现,只有取全模态进行识别时,才能得到较为准确的阻尼系数矩阵,但仍不是精确值;若取的模态值不全,即使是前六阶,在该噪声下的结果仍完全失真,数据失效显著.可以看出复模态虚部的准确度对识别结果能造成影响. 表4 更新前阻尼系数矩阵对角线上数值识别值Tab.4 Values on the diagonal of the damping coefficient matrix identified before the updating 按本文提出的复模态更新方法,对复模态虚部值进行更新后,识别得到的阻尼系数矩阵对角线上数值见表5.从表5中可看出,在对复模态虚部进行更新后,精确识别出阻尼系数矩阵所需要的模态数目增加了,取得全模态便能精确识别出指数阻尼系数矩阵;对复模态进行更新后可以排除噪声对复模态虚部的干扰,反映出本文提出的复模态虚部计算公式(52)能满足阻尼矩阵识别的需要. 表5 更新后阻尼系数矩阵对角线识别值Tab.5 Values on the diagonal of the damping coefficient matrix identified after the updating 取案例1中的7自由度系统研究松弛因子识别式(64)~(66)的准确性.当γ 值较小时,如γ=0.002,该系统更接近于粘滞阻尼系统,按不同方式识别得到的γ 值见图2.从图2中可以看出,这3种识别公式均能较好地识别出松弛因子,按式(65)(66)获得的松弛因子更接近原始值. 当γ 值较大时,如γ=2,此时该体系的阻尼机制表现为明显的非粘滞阻尼特性,按不同方式识别得到的γ 值见图3.从图3中可以看出,这3种识别公式也均能较好地识别出松弛因子,按式(65)获得的松弛因子更接近原始值. 图2 按式(64)~(66)计算的γ 值(原始值γ=0.002)Fig.2 The value of γ calculated by formula(64)~(66)when the original value of γ=0.002 图3 按式(64)~(66)计算的γ 值(原始值γ=2)Fig.3 The value of γ calculated by formula(64)~(66)when the original value of γ=2 本小节将对一根混凝土悬臂梁构件进行锤击振动测试试验,对本文提出的阻尼系数矩阵方法进行研究,并讨论指数阻尼模型的适用性. 该悬臂梁试件配筋和尺寸信息如图4所示.试件采用C35普通混凝土,水泥采用42.5级普通硅酸盐水泥.纵筋采用HRB400级钢筋,抗拉强度设计值为360 MPa,弹性模量为200 GPa;箍筋采用HPB300级光圆钢筋,抗拉强度设计值为270 MPa. 图4 钢筋混凝土悬臂梁试件尺寸及配筋图(单位:mm)Fig.4 Geometry and reinforcement details of reinforced concrete cantilever beam(unit:mm) 该试件的参数为:密度ρ=2.41×103kg/m3,截面积A=0.04 m2,弹性模量E=3.06×1010N/m2,梁长L=0.2 m. 振动试验数据采集设备采用比利时公司的LMS锤击测振系统.振动测试前,将悬臂梁沿梁身均匀取10个锤击作用点,并在顶部粘贴加速度传感器.锤击法振动测试试验示意图见图5.测试时,用力锤依次对所标记的10个测点进行锤击,利用数据采集仪记录下每次锤击时的力传感器信号及加速度响应信号,并计算得到每个锤击点的频响函数平均值.本章的试验完成于湖南大学结构实验室. 图5 锤击振动测试示意图Fig.5 Schematic diagram of hammer vibration test 利用试件实测频响函数曲线,在LMS.Test.Lab软件上进行分析,使用最小二乘复指数法(LSCE)可以估计出试件的频率、阻尼比,并可以计算出相应模态振型. 首先将该试件质量矩阵与刚度矩阵按有限元法进行建模,只研究试件振动方向上的平动自由度,可以得到所需的质量矩阵和刚度矩阵分析值,均为10×10方阵.按照文献[18]提出的迭代算法,对分析质量矩阵与分析刚度矩阵进行修正,可得该试件修正后的质量矩阵M和刚度矩阵K.利用识别得到的前五阶模态参数及修正后的质量矩阵M和刚度矩阵K识别松弛因子μ.按公式(65)计算得到的μ=145.868 s-1. 接下来按本文提出的复模态更新方法对该试验梁进行复模态虚部的更新,并进行指数阻尼系数矩阵识别,识别得到的阻尼系数矩阵如图6所示.由图6可以看出,该识别出的阻尼矩阵的阻尼系数分布不是很明显,可能与试验模态测量误差有关. 图6 悬臂梁阻尼系数矩阵识别值Fig.6 Identification value of damping coefficient matrix of the cantilever beam 悬臂梁试件的前三阶固有频率及阻尼比分别按指数型非粘滞阻尼模型和Rayleigh阻尼模型的识别结果见表6. 表6 悬臂梁前三阶固有频率和阻尼比Tab.6 The first three-order natural frequencies and damping ratios of the cantilever beam 从表6中可以看出,通过文中提出的方法按这两种阻尼模型识别的固有频率均接近试验实测值,但识别得到的阻尼比与实测值有差别.试验测量得到的阻尼比为按单模态识别得到的各测点的每阶模态平均值,而按这两种阻尼模型识别得到的阻尼比为按整体模态计算分析的结果,从而带来识别误差.与按指数阻尼模型计算得到的阻尼比相比,该试验梁采用Rayleigh阻尼模型计算出的第三阶阻尼比与试验实测值相差较大,远大于实测值,这种误差能显著影响结构的动力特性.指数阻尼模型由于参数松弛因子的存在,可以更为合理地拟合结构的阻尼特性. 1)本文提出了指数阻尼系统中对阻尼系数矩阵识别的方法,通过求解一个带约束的优化问题,利用权函数矩阵及初始分析阻尼矩阵,获得满足系统特征方程的阻尼系数矩阵;该方法不需要测得全模态,可以获得比较高的识别精度,但随着系统的非粘滞阻尼特性逐渐增强时,想要精确识别出阻尼系数矩阵所需要的模态数目会逐渐增加;当非粘滞阻尼特性足够大时,最后可能需要取得全模态才能精确识别出阻尼系数矩阵. 2)针对试验噪声对测量得到的复模态虚部精度的影响,本文提出了对复模态虚部进行更新的方法,使之满足指数型阻尼系统特征方程;通过算例分析,将更新前后识别得到的阻尼系数矩阵进行对比,可以看出,提出的阻尼系数矩阵识别公式对噪声较为敏感,且复模态虚部的准确度对阻尼矩阵识别结果影响较大;采用更新后的复模态虚部表达式可以排除阻尼矩阵识别过程中噪声对复模态虚部的影响,且能有效地识别出阻尼系数矩阵;但在对复模态进行更新后,在相同模态阶数下对阻尼系数矩阵的识别精度降低了,并且精确识别所需的模态阶数较多,不使用全模态时识别精度较差,目前的更新方法可以进一步改进. 3)由于目前对松弛因子识别方法的研究较少,且有一定使用限制,本文提出了不依赖于复模态虚部的3种松弛因子识别公式,通过算例分析表明这3种公式均能较高精度地识别出松弛因子,能够满足结构分析的需要. 4)通过对普通C35混凝土悬臂梁进行锤击振动测试,并按本文提出的方法进行模态参数识别,将采用Rayleigh阻尼模型和本文采用的指数型非粘滞阻尼模型识别得到的阻尼比和基本频率进行对比,可发现识别得到的固有频率接近试验实测值,但阻尼比与实测值有差别,采用Rayleigh阻尼模型时第三阶阻尼比出现了很大的误差.指数阻尼模型更能准确合理地描述两根混凝土悬臂梁的阻尼性能.













1.2 权函数的选择

2 复模态更新
2.1 特征方程







2.2 小阻尼系统特征参数

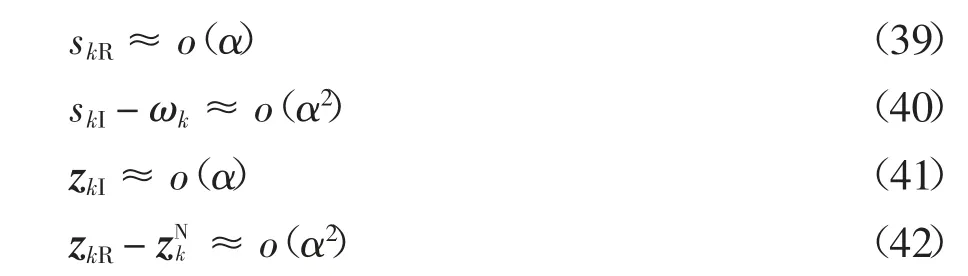

2.3 复模态更新







3 对松弛因子的识别







4 数值算例分析
4.1 案例1:模态参数精确时识别阻尼系数矩阵






4.2 案例2:复模态虚部更新后识别阻尼系数矩阵


4.3 案例3:对松弛因子的识别


5 试验分析
5.1 试验概况


5.2 结构阻尼系数识别


6 结论

