分析空间结构，发展直观想象
——例谈高三空间几何体中垂直关系的复习

浙江安吉县高级中学 (313300) 魏侹路

立体几何教学的一项重要功能在于发展学生的直观想象这一核心素养.什么是直观想象？课程标准中明确指出，它是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.它包括借助空间形式认识事物的位置关系、形态变化与运动规律[1].

空间位置关系中的重点和难点在于垂直关系的探索，空间角中线面角、二面角的寻找关键都在于垂直关系的寻找.学生很多时候不能找出所需的垂直关系，一方面是由于对垂直有关的判定定理和性质定理不熟悉，另一方面是因为对于几何体的认识限于局部、缺少对图形的分析形成整体的感知.所以，帮助学生形成对几何体从整体到局部的认识，从具体到抽象的感知，加强学生对几何体的图形分析能力，对于高三学生的立体几何复习十分重要.下面，笔者结合教学实际，谈谈对高三垂直关系复习的几点想法.

一、借助模型，可以攻玉

分析几何体的空间结构，应当先从分析其表面的平面图形着手.面对复杂的几何体时，有时可以将其分解，产生新的空间几何形体，再正确分析其位置关系与数量关系，并对位置关系和数量关系进行论证与求解.因此，如果在日常学习中注意积累一些简单几何体中的垂直关系，将有助于我们探索复杂几何体中的垂直关系.以下三种模型可以说是非常具有代表性的.

1.墙角模型

定义1 三条棱两两垂直的三棱锥.

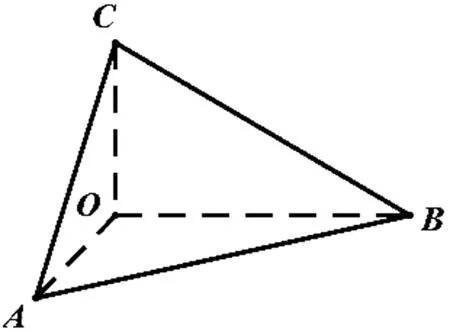
图1

性质1 如图1，三棱锥O-ABC中，OA,OB,OC两两垂直.则三棱锥各个面的垂线如下：显然有OA⊥平面BOC，OB⊥平面AOC，OC⊥平面AOB，容易证明O在平面ABC内的投影为△ABC的垂心H，即OH⊥平面ABC.

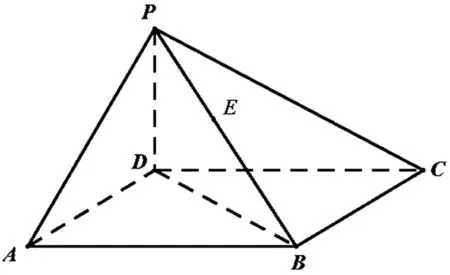
图2

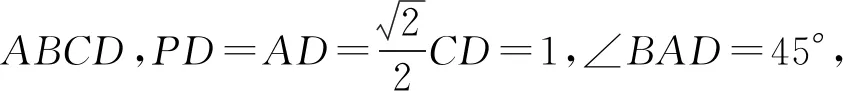
(Ⅰ)求证：DE⊥BC；

(Ⅱ)若平面PAB⊥平面DEC，求出此时PE的长度.

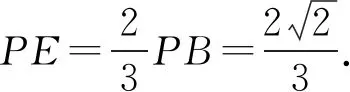
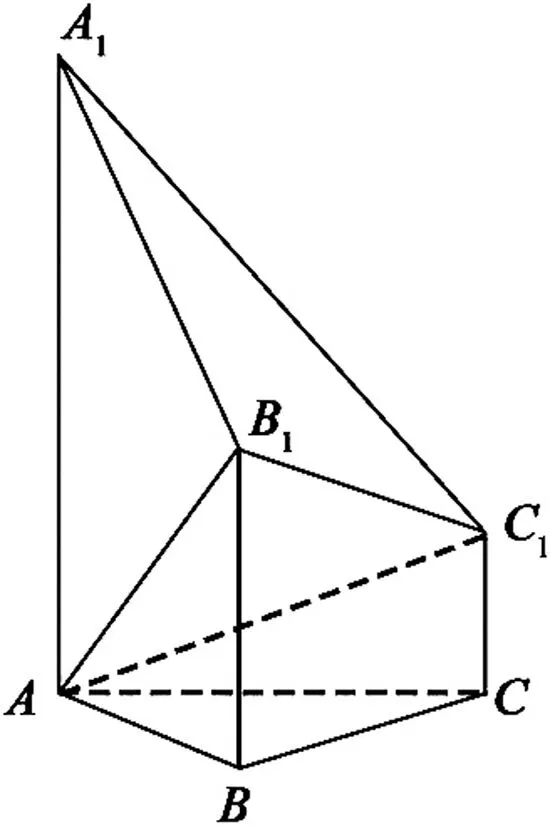
图3

问题2如图3，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2.

(Ⅰ)证明：AB1⊥平面A1B1C1；

(Ⅱ)求直线AC1与平面ABB1所成的角的正弦值.

图4

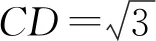
2.鳖臑模型

定义2 四个面都是直角三角形的三棱锥.

性质2 如图5，三棱锥O-ABC中，OA,AB,BC两两垂直.则三棱锥各个面的垂线如下：OA⊥平面ABC，BC⊥平面AOB.作AE⊥OB,BD⊥AC，则AE⊥平面OBC，BD⊥平面OAC.

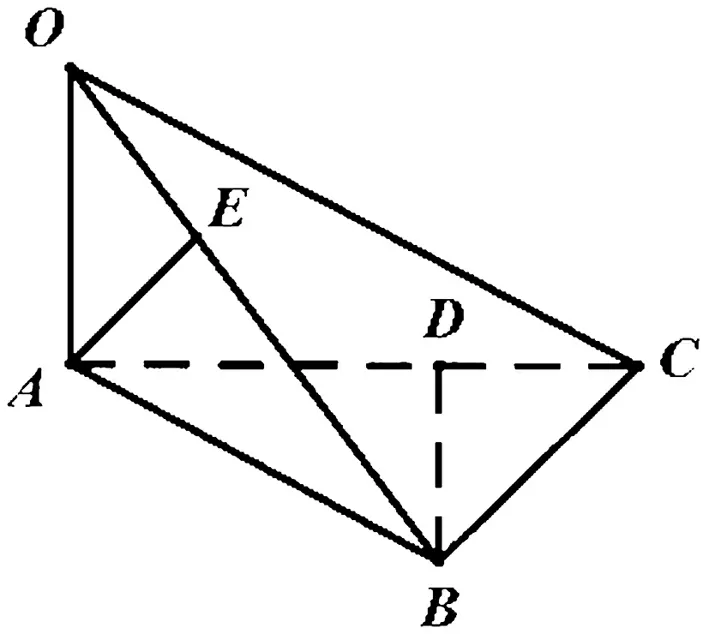
图5

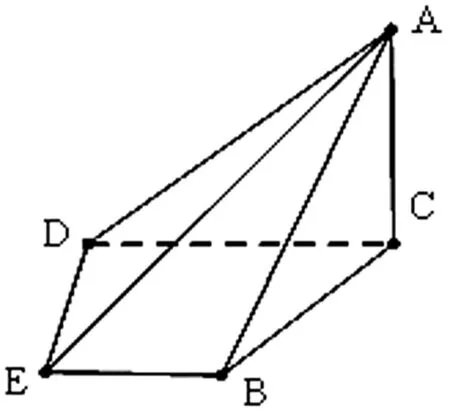
图6

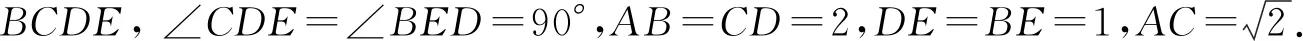
(Ⅰ)证明：EF平面△AEF；

(Ⅱ)求二面角△A′EF的大小.

图7

分析：此题是2014年浙江高考第20题.主要考虑第(Ⅱ)问，此题的常规思路如图7，因为△AED,△ABD均为直角三角形，所以作BF⊥AD于点F，再作FG∥DE交AE于点G，连接BG，则∠BFG即为二面角△A′EF的平面角.虽然此法找出二面角的平面角并不困难，但是BG长度的计算较繁琐.

当连接BD时我们发现，四棱锥A-BCDE被分割成了三棱锥A-BDE和三棱锥A-BDC，而且三棱锥A-BDC就是鳖臑模型.由(Ⅰ)可知面ADE⊥面ADC，故所求二面角即为二面角B-AD-C的余角.根据性质2，二面角B-AD-C在鳖臑体A-BDC中非常容易计算，只需要作BH⊥CD，再作HK⊥AD，连接BK，则∠BKH即为二面角B-AD-C的平面角.(计算过程略)

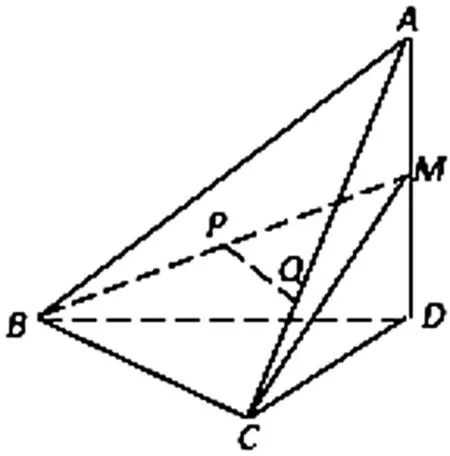
图8

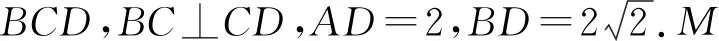
(Ⅰ)证明：PQ∥平面BCD；

(Ⅱ)若二面角C-BM-D的大小为60°，求∠BDC的大小.

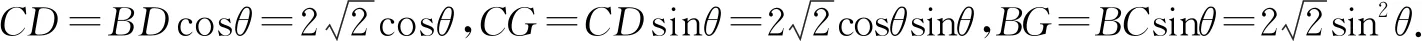
3.对称模型

类似于平面几何中轴对称图形的定义，推广到三维空间中就可以得到“面对称几何体”.

定义3如果空间几何体关于某个平面对称，则称这样的几何体为对称几何体，这个平面叫作该几何体的对称面.

下面以三棱锥为例进行相关的垂直分析.

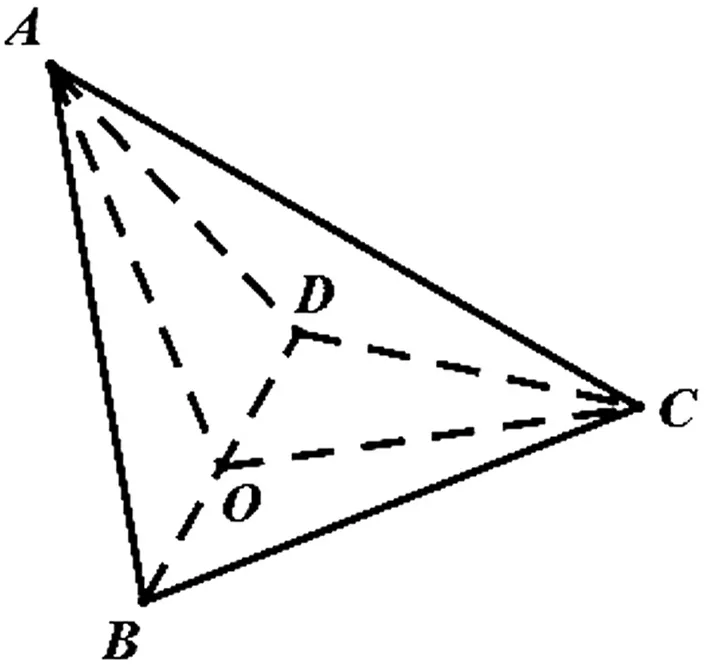
图9

性质3如图9，三棱锥A-BCD中，AB=AD,BC=BD.取BD中点O，则BD⊥平面AOC，进一步可得平面AOC⊥平面ABD，平面AOC⊥平面BCD.

一般的，如果一个多面体是对称几何体，那么它的对称面会垂直于该多面体所有与之相交的表面.

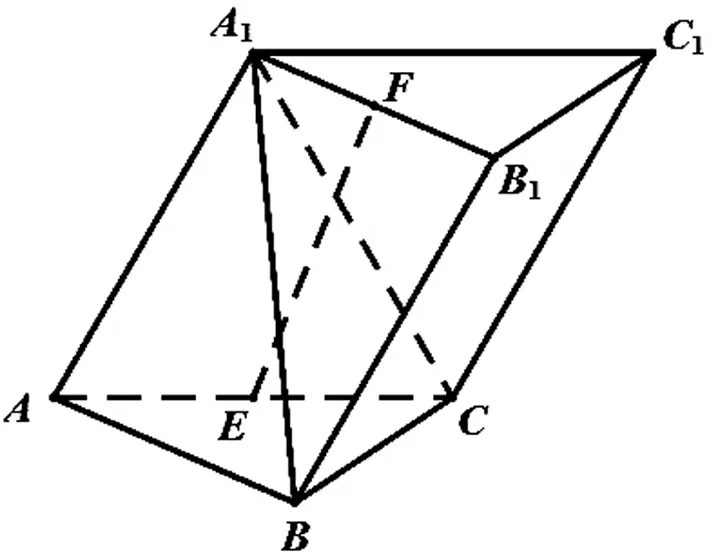
图10

问题5如图10，已知三棱柱ABC-A1B1C1，平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F，分别是AC，A1B1的中点.

(Ⅰ)证明：EF⊥BC；

(Ⅱ)求直线EF与平面A1BC所成角的余弦值.

图11

分析：此问题是2019年浙江高考第19题.因为平面A1ACC1⊥平面ABC，且A1A=A1C=AC，所以A1E⊥平面ABC.注意到E是Rt△ABC的外心，所以A1B=A1C，EB=EC，三棱锥A1-EBC是一个对称几何体.如图11，取BC的中点G，连接EG，FG,A1EGF即为三棱锥A1-EBC的对称面.根据性质3，我们知道平面A1EGF⊥平面A1BC.这个垂直关系的证明不仅解决了第(Ⅰ)问，而且为第(Ⅱ)问也指明了方向——点E在平面A1BC上的投影一定在两个平面的交线A1G上，故∠EOG即为直线EF与平面A1BC所成角(或其补角).(计算过程略)

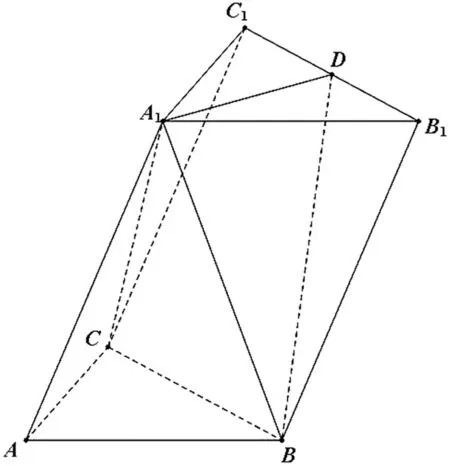
图12

问题6如图12，在三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=2,AA1=4，A1在底面ABC的射影为BC的中点，D为B1C1的中点.

(Ⅰ)证明：A1D⊥平面A1BC；

(Ⅱ)求二面角A1-BD-B1的平面角的余弦值.

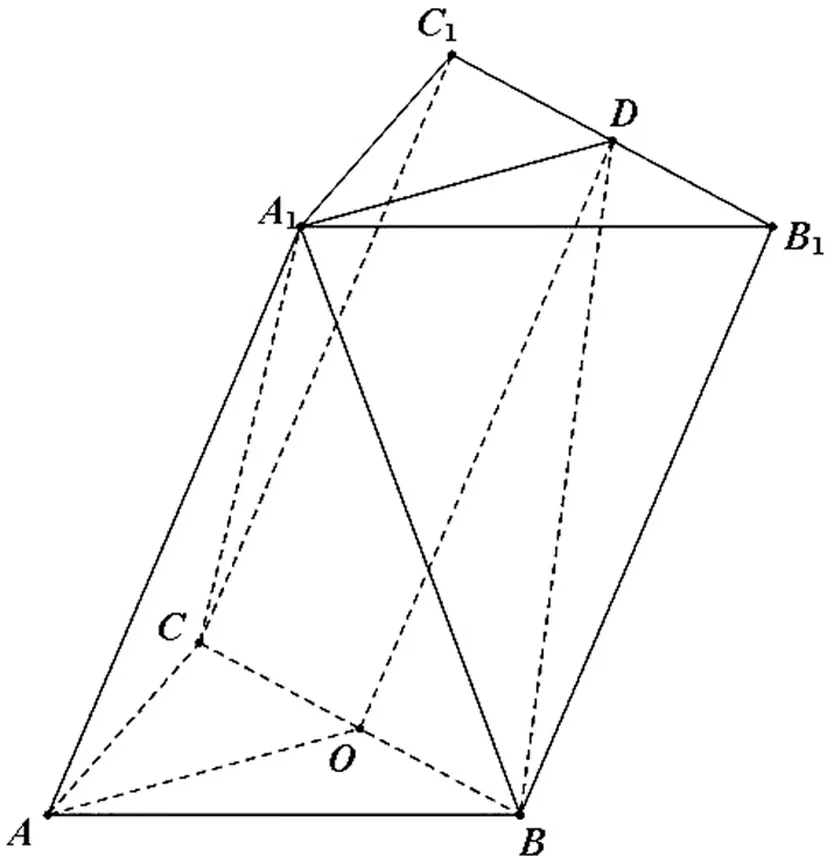
图13

分析：此题是2015年浙江高考第17题，关键要分析出两个垂直关系，一是面A1BC⊥面ABC，这点由“A1在底面ABC的射影为BC的中点”这一已知条件很容易得到，这个垂直关系是解决第(Ⅰ)问的关键.在第(Ⅱ)问中，如果能发现Rt△A1BD≅Rt△B1BD，则二面角的平面角根据定义很快可以作得，这也是当年参考答案给出的解法.这里给出另外一种思路，由“A1在底面ABC的射影为BC的中点，AB=AC”这一已知条件可以知道这个斜三棱柱是一个对称的几何体.所以，根据性质3可知只要取BC的中点O，连接AO,OD，如图13，则这个三棱柱的对称面就是平面AODA1.一旦找到了面B1C1CB的垂面，接下来找二面角A1-BD-B1的平面角就是熟悉的问题了.

二、动态翻折，追根溯源

有时候一些几何体可以看做是某个平面图形翻折而成，那么在分析该几何体的空间结构时，翻折的二面角大小往往是影响几何体形态的关键因素.因此，以翻折所成的二面角为突破口，可以帮助我们从源头上把握几何体中的位置关系和数量关系.

问题7如图14，已知等腰梯形ABCD中AB=4,BC=CD=DA=2，F为线段CD的中点，E，M为线段AB上的点，AE=EM=1.现将四边形AEFD沿EF折起.

(Ⅰ)求证：AM∥平面BCD；

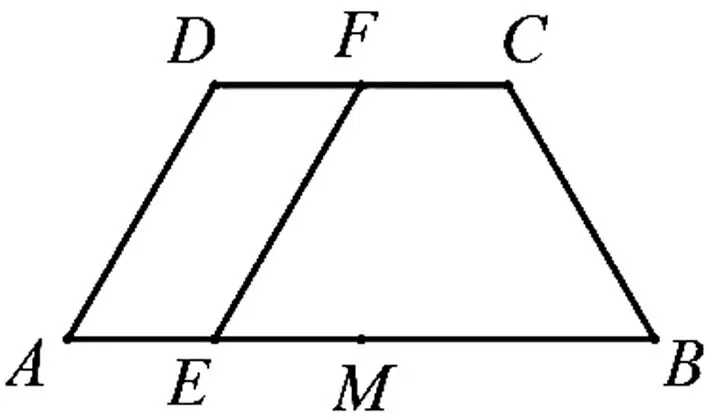
分析：根据题意，多面体ABCDEF是由等腰梯形ABCD翻折而成，翻折后BD的长度决定了翻折的角度，因此二面角D-EF-C的大小是我们分析几何体结构的关键因素.

图15

图16

问题8如图16，已知四棱锥P-ABCD，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点.

(Ⅰ)证明：CE∥平面PAB；

(Ⅱ)求直线CE与平面PBC所成角的正弦值.

分析：此问题是2017年浙江高考第19题，当年这题被称为浙江省高考有史以来最难立体几何题.许多考生由于对于此几何体的结构把握不到位，导致几何方法想不出，向量方法容易建错坐标系.

图17

该几何体可以理解为：如图17，平面内有一个由等腰直角三角形PAD和直角梯形ABCD构成的五边形PABCD，将该五边形沿AD翻折得到的几何体就是四棱锥P-ABCD，其中PC的长度就是用来确定翻折的二面角大小.如果我们先分析五边形PABCD不难发现，PB⊥AD，交点O即为AD的中点，翻折之后∠POB即为二面角P-AD-BC的平面角.而且容易证明BC⊥平面POB，进而平面POB⊥平面PBC.根据PC的长度我们可以确定∠POB=120°.要求直线CE与平面PBC所成角的正弦值，只需要求出点E到平面PBC的距离即可.接下来只需要取BC，PO的中点F，G，将CE平移至FG.这样，就把E到平面PBC的距离转化为G到平面PBC的距离，后面的计算就不再赘述.

转化为常见的几何体模型、用动态翻折的观点看待几何体，能够加强学生对几何体空间结构的分析能力，帮助他们形成对几何体的整体认知，从而更好的探索几何体中的垂直关系，进而发展他们的直观想象这一核心素养.