一类二阶非线性常微分方程组边值问题解的存在唯一性

王 丹, 李永祥

(西北师范大学数学与统计学院, 兰州 730070)

1 引 言

本文讨论二阶非线性常微分方程组边值问题

(1)

解的存在唯一性, 其中非线性函数f,g:[0,1]×R×R→R连续.作为生物种群的常用数学模型,该问题在生物数学等领域有重要应用,不少作者对该问题正解的存在性进行过研究[1-10].常用研究方法主要有文献[1,5,7-10]中的锥上的不动点指数理论, 文献[2-3]中的锥上不动点定理, 以及文献[4,6]中的单调迭代求解方法，等.

1993年，Fink和Gatica[1]运用锥上的不动点指数理论, 在f与g严格单调条件下获得了边值问题

非负解的存在性. 后来, Ma[2]将上述条件弱化为单调条件, 通过举例得到了问题(2)新的非负解的存在性结论. 文献[3]研究了边值问题

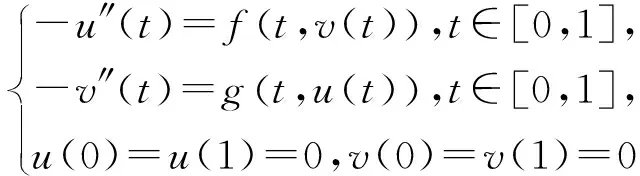
(3)

(该问题的非线性项都是非负的)，在超线性或次线性的条件下获得了正解的存在性. 在上述文献中, 系统正解的存在性均被转化为乘积空间中单锥上相应全连续映射的不动点的存在性.此外，Cheng等[7-10]建立了乘积锥上不动点指数的乘积公式 (见文献[7]中定理2.1), 运用不动点指数的乘积公式在一些超(次)线性假设下获得了几类不同形式的边值问题正解的存在性, 推广了以上结论.

鉴于以上文献都在非线性项f与g各自独立的条件下讨论方程组非负解或正解的存在性，本文则不假设f与g非负, 在f(t,x,y)与g(t,x,y)相关联的不等式条件下运用Leray-Schauder不动点定理获得问题(1)解的存在唯一性. 本文的主要结果如下：

定理1.1设f,g:[0,1]×R×R→R连续.若f,g满足下列条件：

(H1) 存在常数a,b≥0使得a+b<π2及c>0, 使得

f(t,x,y)x+g(t,x,y)y≤

ax2+by2+c,(t,x,y)∈[0,1]×R×R

(4)

则问题(1)至少存在一个解.

加强定理1.1的条件(H1)后, 则有如下存在唯一性结果：

定理1.2设f,g:[0,1]×R×R→R连续.若f,g满足下列条件：

(H2) 存在常数a,b≥0使得a+b<π2,

(f(t,x2,y2)-f(t,x1,y1))(x2-x1)+

(g(t,x2,y2)-g(t,x1,y1))(y2-y1)≤

a(x2-x1)2+b(y2-y1)2

(5)

其中(t,xi,yi)∈[0,1]×R×R,i=1,2, 则问题(1)的存在唯一解.

2 主要结果的证明

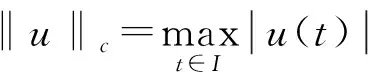
记H1(I)={u∈C(I)|u在I上绝对连续, 且u′∈L2(I)}.

设X,Y分别为范数是‖·‖X,‖·‖Y的Banach空间. 以X×Y表示X与Y的乘积空间按范数‖(x,y)‖=max{‖x‖X,‖y‖Y}构成的Banach空间.

证明 因正弦函数系{sinkπt|k=1,2…}为L2(I)中的完备直交系, 故u可展为正弦级数

其中

且有Parseval等式

另一方面, 余弦函数系{coskπt|k=1,2…}也为L2(I)中的完备直交系, 故u′可展为余弦级数

其中

且有Parseval等式

因而引理2.1成立.

定理1.1的证明 熟知, ∀h∈C(I), 线性二阶边值问题

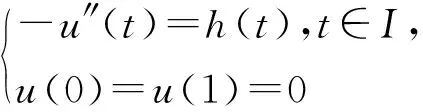
(6)

存在唯一解

其中

为相应的Green函数. 作积分算子A:C(I)×C(I)→C(I)×C(I)为

则A:C(I)×C(I)→C(I)×C(I)为全连续算子, 且问题(1)的解(u,v)等价于算子A的不动点. 我们对A应用Leray-Schauder不动点定理,以证明A有不动点. 为此，考查方程簇

(u,v)=λA(u,v),0<λ<1

(7)

设(u,v)∈C(I)×C(I)为方程簇(7)中某个λ∈(0,1)对应的方程的解.则

(8)

按线性方程解的Green函数表示, (u,v)∈C2(I)×C2(I)满足方程

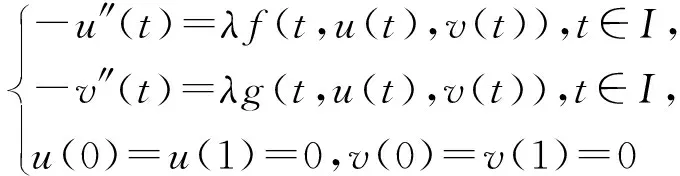
(9)

将方程(9)的第一式和第二式的两边分别同乘以u(t)和v(t), 两式相加, 由条件(H1)可得

-u″(t)u(t)-v″(t)v(t)=λf(t,u(t),

v(t))u(t)+λg(t,u(t),v(t))v(t)≤

λ(au2(t)+bv2(t)+c)≤

au2(t)+bv2(t)+c,t∈I.

上式在I上积分, 左边利用分部积分和方程(9)的边界条件得

由引理2.1,

从而有

所以

因此, ∀t∈I, 有

所以

故

即方程簇(7)的解集在C(I)×C(I)中有界. 由Leray-Schauder不动点定理,A在C(I)×C(I)中有不动点, 该不动点为问题(1)的解.

f(t,x,y)x+g(t,x,y)y=(f(t,x,y)-

f(t,0,0))x+(g(t,x,y)-g(t,0,0))y+

f(t,0,0)x+g(t,0,0)y≤ax2+by2+

|f(t,0,0)x|+|g(t,0,0)y|≤ax2+by2+

C0|x|+C0|y|=ax2+by2+

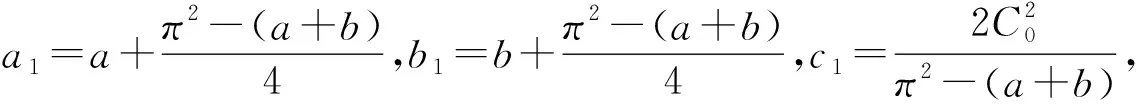
f(t,x,y)x+g(t,x,y)y≤

a1x2+b1y2+c1,(t,x,y)∈I×R×R.

再证解的唯一性. 设(u1,v1),(u2,v2)∈C2(I)×C2(I)为问题(1)的两个解.则有方程

(10)

及

(11)

将方程(11)第一式与方程(10)第一式相减, 方程(11)第二式与方程(10)第二式相减, 得

-(u″2(t)-u″1(t))=f(t,u2(t),v2(t))-

f(t,u1(t),v1(t)),t∈I

(12)

-(v″2(t)-v″1(t))=g(t,u2(t),v2(t))-

g(t,u1(t),v1(t)),t∈I

(13)

将方程(12)两边同乘u2(t)-u1(t), 方程(13)两边同乘v2(t)-v1(t), 两式相加, 由条件(H2)得

-(u″2(t)-u″1(t))(u2(t)-u1(t))-

(v″2(t)-v″1(t))(v2(t)-v1(t))=

(f(t,u2(t),v2(t))-f(t,u1(t),

v1(t)))(u2(t)-u1(t))+(g(t,u2(t),

v2(t))-g(t,u1(t),v1(t)))(v2(t)-

v1(t))≤a(u2(t)-u1(t))2+

b(v2(t)-v1(t))2,t∈I.

上式在I上积分, 左边利用分部积分和方程(10)(11)的边界条件得

即

3 例

例3.1考虑如下二阶微分方程组

方程(14)相应的非线性项为

f(t,x,y)=3x-x3y2+sinπt,g(t,x,y)=

-x2y+6y-2y3+2sinπt

(15)

因为f与g不是非负的, 文献[1-10]的结果对问题(14)不适用.

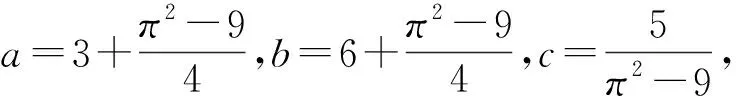
f(t,x,y)x+g(t,x,y)y=3x2-x4y2+

xsinπt-x2y2+6y2-2y4+2ysinπt≤

3x2+6y2+xsinπt+2ysinπt≤3x2+

6y2+|x|+2|y|=3x2+6y2+

ax2+by2+c.

因而f(t,x,y)与g(t,x,y)满足条件(H1). 由定理1.1知方程(14)有解.

例3.2考虑如下二阶微分方程组

方程(16)相应的非线性项为

f(t,x,y)=5x-x3-y+1,g(t,x,y)=

x+4y-y5+t

(17)

下面验证f(t,x,y)与g(t,x,y)满足条件(H2).∀(t,xi,yi)∈[0,1]×R×R,i=1,2. 由(17)式可得

(f(t,x2,y2)-f(t,x1,y1))(x2-x1)+

(g(t,x2,y2)-g(t,x1,y1))(y2-y1)=

(x2-x1)+((x2-x1)+4(y2-y1)-

对函数-x3在x1与x2之间应用微分中值定理得

对函数-y5在y1与y2之间也应用微分中值定理得

结合以上诸式有

(f(t,x2,y2)-f(t,x1,y1))(x2-x1)+

(g(t,x2,y2)-g(t,x1,y1))(y2-y1)=

5(x2-x1)2-3ξ2(x2-x1)2+

4(y2-y1)2-5η4(y2-y1)2≤

5(x2-x1)2+4(y2-y1)2.

因而f(t,x,y)与g(t,x,y)满足条件(H2). 由定理1.2知方程(16)有唯一解.