二次函数中三角形面积与平行四边形问题解析

郭建华

二次函数背景下的三角形面积问题及平行四边形问题是中考的热点题型，下面举例进行分析，以帮助同学们总结规律，探寻通法.

原题再现

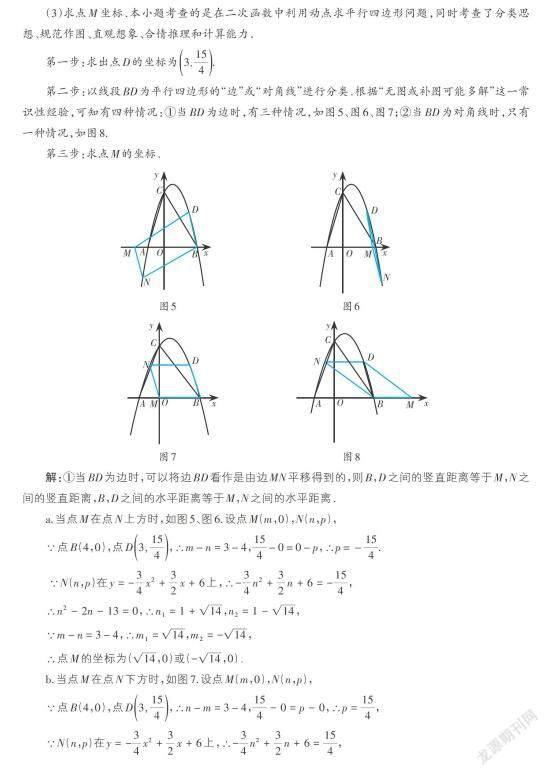
例（2020·甘肃·天水·第26题）如图1所示，拋物线y=ax2 + bx + c（a ≠ 0）与x 轴交于A，B 两点，与y轴交于点C，且点A 的坐标为（-2，0），点C 的坐标为（0，6），对称轴为直线x=1. 点D 是抛物线上一个动点，设点D 的横坐标为m（1

（1）求抛物线的函数表达式.

（2）当△BCD 的面积等于△AOC 的面积的34时，求m 的值.

（3）在（2）的条件下，若点M 是x 轴上一动点，点N 是抛物线上一动点，试判断是否存在这样的点M，使得以点B，D，M，N 为顶点的四边形是平行四边形. 若存在，请直接写出点M 的坐标;若不存在，请说明理由.

分析与拓展

（1）求抛物线的解析式. 本小题考查核心知识点的掌握情况，即待定系数法、解方程组. 求抛物线解析式一般有三种方式可供选择，即一般式、交点式、顶点式，本题应选用一般式求解. 可得抛物线的函数表达式为y = -34x2 +32x + 6（过程略）.

（2）求m 的值. 本小题考查的是在平面直角坐标系中，给定函数图形和几何图形（三角形），求点的坐标（横坐标）;同时也考查了推理论证、计算能力和答题过程的严谨性.

第一步：根据三个顶点的坐标O（0，0），A（-2，0），C（0，6）直接求出△AOC 的面积.

第二步：求不平行于坐标轴的△BCD（即△BCD 的三边DB，DC，BC 都不平行于坐标轴，简称“斜线三角形”）的面积一般采用割补法;过动点D 作x 轴的垂线，利用割补法将原三角形DBC 分成△DEB 和△DEC，如图2，使得这两个三角形可以利用“铅垂高× 水平宽”求解.

第三步：①求未知直线BC 的函数表达式;②利用垂直于x 轴的直线上任意两点横坐标相等，将其纵坐标相减求出铅垂线段.

第四步：列方程求解.

详细解答如下：

解：如图2，过点D 作DE⊥x 轴于F，交BC 于E，过点C 作CH⊥ED，交ED 的延长线于H，

∵点A 的坐标为（-2，0），点C 的坐标为（0，6），

∴OA=2，OC=6，∴S△AOC =12OA ⋅ OC =12× 2 × 6 = 6，

∴S△BCD =34S△AOC =34× 6 =92.

易得點B 的坐标为（4，0），设直线BC 的函数表达式为y=kx + n，

则

ìíî

4k + n = 0，

n = 6，

解得ìíîïïk = -32，n = 6， ∴直线BC 的函数表达式为y = -32x + 6，

∵点D 的横坐标为m（1

∴DE = yD - yE = （ ） -34m2 +32m + 6 - （ ） -32m + 6 = -34m2 + 3m，

∵S△BCD = S△CDE + S △BDE，∴S△BCD =12DE ⋅ HC +12DE ⋅ BF =12DE ⋅ OF +12DE ⋅ BF =12DE ⋅ OB，

∴ S△BCD =12（ ） -34m2 + 3m × 4 = -32m2 + 6m，∴-32m2 + 6m =92，

解得：m1=1（不合题意舍去），m2=3. 则当△BCD 的面积等于△AOC 的面积的34时，m 的值为3.

拓展：（1）本题中若将限制条件“1

如：当点D 在点C 左侧抛物线上时（如图3），S△DBC =12DE （ BF - OF ） =12DE ⋅ OB;当点D 在抛物线第四象限部分上时（如图4），S△DBC =12DE（CH - BF）=12DE·OB.

（3）求点M 坐标.本小题考查的是在二次函数中利用动点求平行四边形问题，同时考查了分类思想、规范作图、直观想象、合情推理和计算能力.

第一步：求出点D的坐标为（3， 15）4 .

第二步：以线段BD 为平行四边形的“边”或“对角线”进行分类.根据“无图或补图可能多解”这一常识性经验，可知有四种情况：①当BD 为边时，有三种情况，如图5、图6、图7;②当BD 为对角线时，只有一种情况，如图8.

第三步：求点M 的坐标.

解：①当BD 为边时，可以将边BD 看作是由边MN 平移得到的，则B，D 之间的竖直距离等于M，N 之间的竖直距离，B，D 之间的水平距离等于M，N 之间的水平距离.

a.当点M 在点N 上方时，如图5、图6.设点M（m，0），N（n，p），

∵点B（4，0），点D（3， 15）4 ，∴m-n = 3-4，154 -0=0-p，∴p=-154 .

∵N（n，p）在y = -34x2 +32x + 6上，∴-34n2 +32n + 6 = -154 ，

∴n2 - 2n - 13 = 0，∴n1 = 1 + 14，n2 = 1 - 14，

∵m-n = 3-4，∴m1 = 14，m2 = - 14，

∴点M 的坐标为（ 14，0）或（- 14，0）.

b.当点M 在点N 下方时，如图7.设点M（m，0），N（n，p），

∵点B（4，0），点D（3， 15）4 ，∴n-m = 3-4，154 - 0 = p - 0，∴p = 154 ，

∵N（n，p）在y = -34x2 +32x + 6上，∴-34n2 +32n + 6 = 154 ，

∴n2 - 2n - 3 = 0，∴n1 = 3（舍），n2 = -1，

∵n-m = 3-4，∴m = 0，

∴点M 的坐标为（0，0）.

②当BD 为对角线时，如图8，我们可以发现ND⫽BM，则点N 的纵坐标等于点D 的纵坐标;再根据平移即可求出点M 坐标.

设点M（m，0），N（n，p），

∵点B（4，0），点D（3， 15）4 ，

∴n-3 = 4-m，154 - 0 = p - 0，∴p = 154 .

∵N（n，p）在y = -34x2 +32x + 6上，

∴-34n2 +32n + 6 = 154 ，

∴n2 - 2n - 3 = 0，∴n1 = 3（舍），n2 = -1，

∵n-3 = 4-m，∴m = 8，∴点M 的坐标为（8，0）.

綜上，点M 的坐标为（ 14，0）或（- 14，0）或（0，0）或（8，0）.

本题小结：在平面直角坐标系中，解决平行四边形问题，可以利用平行四边形的性质求解，也可以转化成平移问题.

跟踪巩固

如图9，直线y = -34x + 3与x 轴交于点C，与y 轴交于点B，抛物线y = ax2 +34x + c 经过B，C 两点.

（1）求抛物线的解析式;

（2）如图9，点E 是直线BC 上方抛物线上的一个动点，当△BEC 面积最大时，请求出点E 的坐标和△BEC 面积的最大值.

（3）在（2）的结论下，过点E 作y 轴的平行线交直线BC 于点M，连接AM，点Q 是抛物线对称轴···上的动点，在抛物线上是否存在点P，使得以P，Q，A，M 为顶点的四边形是平行四边形？如果存在，请直接写出点P 的坐标;如果不存在，请说明理由.

（作者单位：本溪市实验中学）