考虑输出约束的机械臂命令滤波反步控制

林孟豪,张蕾,李鹏飞,王晓华,王文杰

(西安工程大学电子信息学院,710048,西安)

柔性关节机械臂具有高适应性、低能耗、质量轻等特点,能够代替人类在航天、高精度制造工艺、医疗等领域进行复杂、危险的工作[1-2]。然而,随着关节数量的增加,会导致柔性关节机械臂的响应速度、轨迹跟踪精度等问题变得更加复杂。另外,由于单连杆柔性关节机械臂灵敏度低、应用范围受限,因此降低了单连杆柔性关节机械臂控制策略研究的应用价值。因此,研究双连杆柔性关节机械臂的轨迹跟踪响应速度、轨迹跟踪控制精度等问题具有重要的理论意义和应用价值。

针对以上问题,文献[3]较早地设计出PD自适应控制器,提高了柔性关节机械臂的轨迹跟踪精度,但是并未考虑机械臂系统的稳定性问题。文献[4]提出了混合控制策略,优化控制器的设计,并生成混合轨迹,虽然提高了柔性关节机械臂系统的鲁棒性,但是没有考虑机械臂的轨迹跟踪精度。文献[5]提出一种模糊优化控制方法,设计出自适应鲁棒控制器,确保了柔性关节机械臂轨迹跟踪精度,并提高了鲁棒性,但是没有考虑机械臂的轨迹跟踪响应速度问题。文献[6]针对机械臂参数不确定影响轨迹跟踪性能的问题,采用两个RBF神经网络同时处理不确定参数,显著提高了轨迹跟踪性能,但并未考虑扰动误差对机械臂系统的影响。文献[7]通过设计一种基于奇异摄动理论的有界控制器,采用模糊逻辑控制参数自动调整,保证了柔性关节机械臂的轨迹跟踪精度和响应速度,但是却增加了机械臂系统的计算复杂度。然而,上述研究内容均未考虑柔性关节机械臂系统的输出约束与计算复杂等问题对提高机械臂系统轨迹跟踪响应速度与轨迹跟踪精度的影响。

为了保证机械臂系统的轨迹跟踪精度,需要将系统的跟踪误差约束在预先设定的范围内。目前针对此类研究的方法主要有模型预测控制[8],Funnel控制[9]和障碍李雅普诺夫函数(barrier Lyapunov function,BLF)[10]等。文献[11]基于常对数型障碍李雅普诺夫函数,提出全状态反馈神经网络控制策略,保证了柔性关节机械臂的轨迹跟踪精度,提高了系统的鲁棒性,但并未考虑机械臂系统的轨迹跟踪响应速度问题。文献[12]基于时变正切型障碍李雅普诺夫函数,提出了一种自适应控制策略,解决了带有输出约束和模型不确定的柔性关节机械臂轨迹跟踪响应速度较慢的问题。然而,障碍李雅普诺夫函数的应用会造成系统的计算难度增大。文献[13]针对柔性关节机械臂计算量大、计算困难等问题,设计了命令滤波控制器,降低了计算难度,但是该方法并没有考虑到命令滤波器带来的滤波误差对整个控制系统的影响。

鉴于上述分析,本文提出一种具有输出约束和误差补偿的双连杆柔性关节机械臂命令滤波反步控制(barrier Lyapunov function with command-filtered backstepping control,BLF-CFBC)策略。首先采用常对数型障碍李雅普诺夫函数设计虚拟控制函数,约束机械臂系统的轨迹跟踪误差;接着采用命令滤波器得到滤波后的虚拟控制函数及其导数,降低反步法中的计算维度,并引用滤波补偿机制,减少滤波误差对整体系统的影响;最后,通过仿真实验,证明了本文所提控制策略能够达到提高双连杆柔性关节机械臂系统轨迹跟踪响应速度与轨迹跟踪精度的控制目标。本文主要创新点如下:

(1)利用常对数型障碍李雅普诺夫函数解决了双连杆柔性关节机械臂系统的输出约束问题;

(2)在双连杆柔性关节机械臂模型反步递推控制律过程中,采用命令滤波器降低了计算复杂度;

(3)通过引入误差补偿机制减少了采用命令滤波器带来的误差,并证明了系统补偿后的跟踪误差有界性。

1 系统描述与控制目标

本文以双连杆柔性关节机械臂模型作为被控对象,其结构示意图如图1所示。

图1 双连杆柔性关节机械臂示意图

根据文献[14],建立双连杆柔性关节机械臂系统的动力学模型如下

(1)

(2)

假设1[15]矩阵M(qi)(i=1,2)∈Rn×n为正定对称矩阵。

假设2[15]期望轨迹qdi(i=1,2)及其导数连续且有界。

本文的控制目标是设计一个具有输出约束和误差补偿的双连杆柔性关节机械臂命令滤波反步控制策略,在保证系统中所有信号有界的前提下,使得系统的输出qi(i=1,2)可以跟踪期望轨迹qdi(i=1,2),并且跟踪误差qi-qdi(i=1,2)可以收敛到原点附近的一个领域内。

2 命令滤波及障碍李雅普诺夫函数

本文所采用的二阶命令滤波器定义如下[16]

(3)

本文所采用障碍李雅普诺夫函数定义如下。

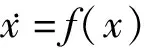
定义2[18]传统对数型障碍李雅普诺夫函数表达式为

(4)

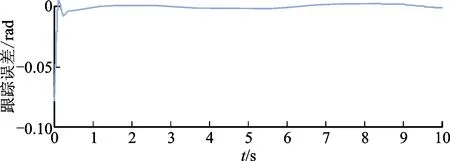
式中:ln(·)为自然对数,i=1,2,3,4;vi为系统误差变量;kbi>0为约束边界,满足|v(0)|

引理1[19]对任意常数kbi,若Z1={z1∈R:-kb1

(5)

式中:η=[ω,z1]T∈M,ω∈Rl,t∈R+,h为在定义域中关于t分段连续且满足局部Lipschitz条件。假设存在函数U:Rl→R+和V1:Rl→R+在各自定义域上连续可微且正定,那么:

V1(z1)→∞,z1→-kb1或z1→Kb1

(6)

γ1(‖ω‖)≤U(‖ω‖)≤γ2(‖ω‖)

(7)

式中,γ1(·)、γ2(·)为K∞函数。取V(η)=V1(z,t)+U(ω),z1(0)∈Z1,则

(8)

成立,故z1(t)有界,z1∈(-kb1,kb1),∀t∈[0,+∞),系统的解η(t)一致最终有界,并且当t→∞时,zi(t)→0,(i=1,2,…,n)。

3 控制器设计

在本节中,针对式(1)双连杆柔性关节机械臂模型,设计具有输出约束和误差补偿的命令滤波反步控制(BLF-CFBC)策略,使得双连杆柔性关节机械臂的输出轨迹能够精准跟踪期望轨迹。

控制器具体设计思路如下:

(1)对双连杆柔性关节机械臂动力学模型式(1),选取系统的状态变量并转换为四阶系统模型式(2),再采用反步法对系统模型进行降阶,选取状态变量作为虚拟控制输入,设计系统误差变量;

(2)在思路(1)的基础上对前两阶子系统引入障碍李雅普诺夫函数,解决系统输出约束问题;

(3)在思路(2)的基础上通过采用命令滤波器得到虚拟控制函数及其导数,降低系统控制器的设计复杂度并引入误差补偿机制降低滤波误差对系统的影响。

定义系统误差变量为:z1i=x1i-x1di(i=1,2),z2i=x2i-α1i,c(i=1,2),z3i=x3i-α2i,c(i=1,2),z4i=x4i-α3i,c(i=1,2),其中x1di=gdi(i=1,2),αxi(x=1,2,3;i=1,2)为虚拟控制函数,αxi,c(x=1,2,3;i=1,2)为经过命令滤波器后的虚拟控制函数。由于命令滤波器的使用会产生滤波误差,从而影响系统的整体性能。本文通过引入误差补偿变量来控制滤波误差对系统的整体影响。

由文献[21]可知,定义补偿后的误差变量为

v1i=z1i-ζ1i(i=1,2),v2i=z2i-ζ2i(i=1,2)

v3i=z3i-ζ3i(i=1,2),v4i=z1i-ζ4i(i=1,2)

本文采用反步法逆推地设计控制器,设计过程分为以下4个步骤。

第1步选取补偿后的误差变量为

v1i=z1i-ζ1i

(9)

对式(9)求导

(10)

根据定义1和定义2,构造障碍李雅普诺夫函数为

(11)

对式(11)求导,得

(12)

设计虚拟控制函数α1i(i=1,2)和误差补偿变量ζ1i(i=1,2)的导数为

(13)

(14)

式中:k1∈Rn×n为正定对称常数矩阵。

将式(13)(14)代入式(12),可得

(15)

第2步选取补偿后的误差变量

v2i=z2i-ζ2i

(16)

对式(16)求导

(17)

构造李雅普诺夫函数为

(18)

对式(18)求导,得

(19)

设计虚拟控制函数α2i(i=1,2)和误差补偿变量ζ2i(i=1,2)的导数为

(20)

(21)

式中k2∈Rn×n为正定对称常数矩阵。

通过引理3,将式(20)(21)代入(19),可得

(22)

第3步选取补偿后的误差变量为

v3i=z3i-ζ3i

(23)

对式(23)求导,得

(24)

构造李雅普诺夫函数为

(25)

对式(25)求导,得

(26)

设计虚拟控制函数α3i(i=1,2)和误差补偿变量ζ3i(i=1,2)的导数为

(27)

(28)

式中,k3∈Rn×n为正定对称常数矩阵。

将式(27)(28)代入(26)可得

(29)

第4步选取补偿后的误差变量为

v4i=z4i-ζ4i

(30)

对式(30)求导,得

(31)

构造李雅普诺夫函数为

(32)

对式(32)求导,得

(33)

在这一步中出现了系统的真实控制函数,设计控制律τ为

(34)

根据文献[21]设计系统的误差补偿变量ζ4i(i=1,2)的导数为

(35)

式中,k4∈Rn×n为正定对称常数矩阵。

将式(34)(35)代入(33),可得

(36)

4 稳定性证明

(37)

式中,a为任意常数。

选取整个系统的李雅普诺夫函数为

(38)

对式(38)求导,得

(39)

通过引理2,将虚拟控制律(13)(20)(27)和控制律(34)代入式(39),得

(40)

(41)

由引理4可知,式(41)的解为

Vs(t)≤e-φ(t-t0)V(t0)

(42)

由式(42)可得,Vs指数收敛至零,收敛速度取决于φ,并且当t→∞时,z1i→0(i=1,2),z2i→0(i=1,2),z3i→0(i=1,2),z4i→0(i=1,2)。

由补偿后的误差变量定义可知

vxi=zxi-ζxi(x=1,2,3,4;i=1,2)

(43)

(44)

根据k0的定义以及引理1可知,通过调节命令滤波参数与设计参数ki(i=1,2,3,4)可以保证系统补偿后的跟踪误差v1i(i=1,2)有界,且能够收敛到原点附近的一个领域内。

由控制律表达式(34)可知系统控制器输出有界,根据假设1与假设2,通过调用引理1,可证得补偿后的机械臂系统所有闭环信号可保证一致最终有界。由于Vs(t)有界,∀t≥0,根据定义1与定义2可得V1(z1i)→∞(i=1,2),|z1i|→kb1(i=1,2),|z1i|≠kb1,即输出约束得到满足。

5 仿真验证

为了验证本文所提BLF-CFBC控制策略的有效性,对图1所示的双连杆柔性关节机械臂模型进行数值仿真。并将仿真结果与不具有输出约束和误差补偿的双连杆柔性关节机械臂命令滤波反步控制策略(CFBC)的结果进行对比,其中CFBC与BLF-CFBC策略的参数设计如下

(45)

(46)

(47)

(48)

式中

(49)

(50)

(51)

其中q1、q2为机械臂关节的旋转角度,g为重力加速度。

图2 关节1轨迹跟踪响应曲线

图2为CFBC策略与BLF-CFBC策略下,双连杆柔性关节机械臂关节1的轨迹跟踪响应曲线图。其中,CFBC策略下关节1在0.1 s后能够跟踪上期望轨迹曲线,而BLF-CFBC策略在0.08 s就能够跟踪上期望轨迹曲线,轨迹跟踪响应速度提升20%。

图3表示CFBC策略与BLF-CFBC策略下,双连杆柔性关节机械臂关节2的轨迹跟踪响应曲线图,从图中可以看出,CFBC策略下关节2在0.2 s后才能跟踪上期望轨迹曲线,本研究所提BLF-CFBC策略下,关节2在0.14 s后能够跟踪上期望轨迹曲线,其轨迹跟踪响应速度提升了30%。

图3 关节2轨迹跟踪响应曲线

图4表示CFBC策略下,双连杆柔性关节机械臂关节1与关节2的轨迹跟踪误差曲线图,图5表示BLF-CFBC策略下,双连杆柔性关节机械臂关节1与关节2的轨迹跟踪误差曲线图。

(a)关节1

(b)关节2

由图4、5可知,对于双连杆柔性关节机械臂系统,CFBC策略的轨迹跟踪误差较大,而本文所提BLF-CFBC策略的轨迹跟踪误差明显减小。由于障碍李雅普诺夫函数的应用,可将轨迹跟踪误差约束在-kb与kb之间,kb>0为约束边界,并且在误差波形稳定后,相比于CFBC策略,在BLF-CFBC策略下关节1的轨迹跟踪误差减少4%,关节2的轨迹跟踪误差减小3.5%,表明所提控制策略有效地提高了机械臂系统的轨迹跟踪精度。

图6为CFBC策略下双连杆柔性关节机械臂关节1与关节2的控制力矩曲线图。

(a)关节1

图7为本文所提BLF-CFBC策略下关节1与关节2的控制力矩曲线图。综合图6和图7可见,本文所提BLF-CFBC策略,控制力矩曲线峰值较小,意味着对机械臂中的电机损耗较小,而CFBC策略下控制力矩曲线峰值较大,可能会对机械臂中的电机造成强烈冲击。

(a)关节1

综合以上仿真结果可以得出:本文所提BLF-CFBC策略与CFBC策略相比较,双连杆柔性关节机械臂的轨迹跟踪响应速度与轨迹跟踪精度有明显的提高,能够达到较好的控制目标。

6 结 论

本文以提高柔性关节机械臂轨迹跟踪响应速度和控制精度为目标,提出一种在常规反步控制算法中结合对数型障碍李雅普诺夫函数和命令滤波器算法的控制策略。通过构造障碍李雅普诺夫函数加快轨迹跟踪速度,同时将轨迹跟踪误差约束在设定的误差范围内;通过引入命令滤波器避免了常规反步法在高阶系统设计时对控制变量反复求导导致的计算爆炸的问题;设计命令滤波器误差补偿机制以削弱采用滤波器产生的误差对跟踪精度的影响。理论证明验证了本文所设计的控制策略可以保证轨迹跟踪误差的有界约束和所有闭环系统中的信号的一致最终有界。仿真结果表明,本文所提策略相比于不具有输出约束和误差补偿的命令滤波反步控制策略,其控制精度和跟踪误差收敛时间都有提高。

未来的工作将会考虑在状态变量部分未知的情况下,引入观测器设计等控制算法[24-25],从而克服本文所提策略中所有状态变量必须全部已知的约束条件。