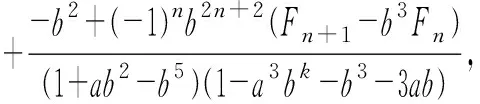广义Fibonacci数列的若干和公式
曾文建
(福建信息职业技术学院 基础教学部,福建 福州 350007)
Fibonacci数列是典型的递推关系数列,在数学理论研究和实际应用中起着重要的作用,不少学者重视该数列并对其特性进行了深入细致的研究,得到许多重要、有趣的性质[1-3],使其在优选法、计算机科学、人口理论、最优化理论、数据处理等领域得到广泛的运用。广义Fibonacci数列形式多样,有很多好的性质[4-5],学者们也推出一些很好的恒等式,如文献[6-7]给出广义Fibonacci数列的一些组合恒等式,文献[8-9]给出广义Fibonacci数的若干恒等式。笔者利用递推关系对广义Fibonacci进一步研究,得到一些新的和公式。
1 预备知识
定义[10]如果对任意实数a,b及n=1,2,3,…, 有F0=0,F1=1,…,Fn+1=aFn+bFn-1,称该数列为广义Fibonacci数列。
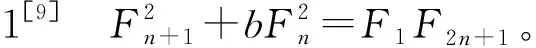
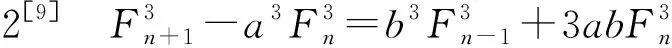
+3a(-b)nFn。
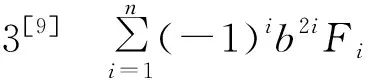
2 定理证明
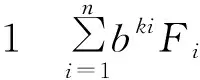
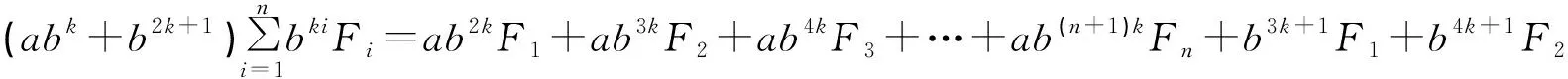
+b5k+1F3+…+b(n+2)k+1Fn
=ab2k+b3k(aF2+bF1)+b4k(aF3+bF2)+…+b(n+1)k(aFn+bFn-1)+b(n+2)k+1Fn
=ab2k+b3kF3+b4kF4+…+b(n+1)kFn+1+b(n+2)k+1Fn
由定义有F1=1,F2=a,代入上式,移项化简得

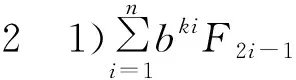
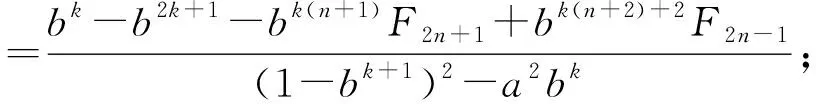
证明:令u=bkF1+b2kF3+…+bnkF2n-1,
v=bkF2+b2kF4+…+bknF2n。
则(1-bk+1)u=bkF1+b2kF3+…+bnkF2n-1
-(b2k+1F1+b3k+1F3+…+b(n+1)k+1F2n-1)
=bkF1+b2k(F3-bF1)+b3k(F5-bF3)+…
+bkn(F2n-1-bF2n-3)-bk(n+1)+1F2n-1
=bkF1+b2kaF2+b3kaF4+…+bknaF2n-2
-bk(n+1)+1F2n-1
=bkF1+abk(bkF2+b2kF4+…+bk(n-1)F2n-2)
-bk(n+1)+1F2n-1
=bk+abkv-bk(n+1)aF2n-bk(n+1)+1F2n-1
=bk+abkv-bk(n+1)(aF2n+bF2n-1)
=bk+abkv-bk(n+1)F2n+1。
(1-bk+1)v=bkF2+b2kF4+…+bknF2n-(b2k+1F2
+b3k+1F4+…+b(n+1)k+1F2n)
=bkF2+b2k(F4-bF2)+b3k(F6-bF4)+…
+bkn(F2n-bF2n-2)-b(n+1)k+1F2n
=bkF2+b2kaF3+b3kaF5+…+bknaF2n-1
-bk(n+1)+1F2n
=bkF2+au-abkF1-bk(n+1)+1F2n,由定义有
F1=1,F2=a,代入得
(1-bk+1)v=au-bk(n+1)+1F2n,
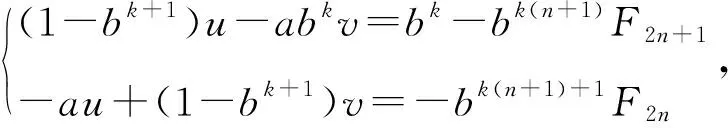
当(1-bk+1)2-a2bk≠0时, 令D=(1-bk+1)2-a2bk,
=bk-b2k+1-bk(n+1)F2n+1+bkn+2k+1F2n+1
-abkn+2k+1F2n
=bk-b2k+1-bk(n+1)F2n+1+bkn+2k+2F2n-1,
=-bk(n+1)+1F2n+bkn+2k+2F2n+abk-abk(n+1)F2n+1
=abk-bk(n+1)(aF2n+1+bF2n)+bkn+2k+2F2n
=abk-bk(n+1)F2n+2+bkn+2k+2F2n。
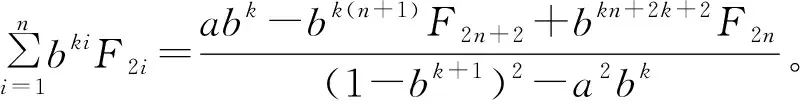
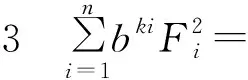
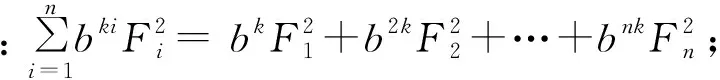
(1)
(2)
由(1)+(2)得
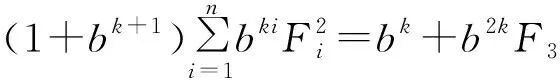
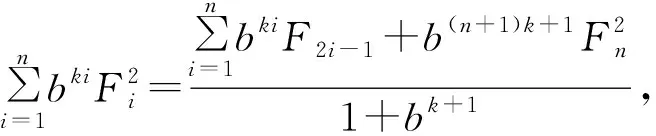
定理得证。
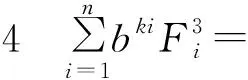
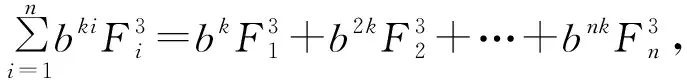
(3)
(4)
由(3)-(4)得
由引理2得
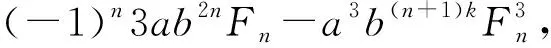
由引理3,代入上式化简得