集值混合变分不等式的一类自适应惯性投影次梯度算法

刘丽平, 彭建文

(重庆师范大学数学科学学院, 重庆 401331)

1.引言

设H是一实Hilbert空间, 其内积和范数分别表示为〈·,·〉和‖ · ‖,K ⊂H是非空闭凸集.设f:H →R∪{+∞}是一个真凸下半连续函数且T:K →2H是一个集值映射.在本文中, 我们考虑如下的集值混合变分不等式问题(简记为SMVIP(T,K)): 求x* ∈K,且存在ω* ∈T(x*),使得

我们用Sol(T,K)表示SMVIP(T,K)的解集.

对SMVIP(T,K)的研究已经引起了广泛的关注.[1-5,14,17]下面各种问题可以看作是问题(1.1)的特殊情况.

显然, 若f= 0, 则SMVIP(T,K)退化为如下集值变分不等式问题[6-8]: 求x* ∈K, 且存在ω* ∈T(x*), 使得

其次, 设φ:K →R∪{+∞}是连续凸函数, 令T=∂φ, 其中∂φ是φ的次微分, 则x* ∈K是SMVIP(T,K)的解的充分必要条件为:x* ∈K是如下的不可微优化问题:

的解.

当T是单值映射时,ω*=T(x*),则SMVIP(T,K)退化为如下的混合变分不等式问题[9-10]:求x* ∈K, 使得

进一步地, 若函数f= 0, 则混合变分不等式问题(1.4)就退化为经典的变分不等式问题[11-12]: 求x* ∈K, 使得

XIA等[5]引入了一类投影次梯度方法来求解集值混合变分不等式问题(1.1), 并在T为仿单调和Lipschitz连续映射的假设条件下, 证明了由投影次梯度方法所产生的序列弱收敛于集值混合变分不等式问题(1.1)的解.最近, Anh和Vinh[11]在Hilbert空间中提出了一类自适应惯性投影梯度算法来求解单调且半连续或强伪单调经典变分不等式(1.5), 该算法的步长是动态选择的, 且在不与混合/粘度或线搜索方法相结合的情况下, 获得了强收敛性的结果.

因此, 为求解集值混合变分不等式问题(1.1), 我们在Hilbert空间中引入了一类新的自适应惯性投影次梯度方法.该算法的优点是, 步长是动态选择的, 并且增加了惯性项以加速收敛特性.在集值映射T是f-强伪单调或单调且H-半连续的假设条件下, 我们证明了由该新算法所产生的序列强收敛于集值混合变分不等式问题(1.1)的解.

2.预备知识

在这一节, 我们回顾或给出本文所需的定义和引理.

定义2.1[13]设T:K →2H是一集值映射.

1)T称为闭图象的, 如果其图象

graph(T)={(x,y)∈K×H:x ∈K,y ∈T(x)}

是K×H中之一闭集;

2)T称为在集合U(⊂K)上是紧的, 如果是H中的相对紧集.

定义2.2[14]设f:K →R∪{+∞}是一个真凸下半连续函数,T:K →2H是一集值映射.则映射T称为

1) 在K上单调的, 若对∀(x,x*),(y,y*)∈graphT有:

2) 在K上仿单调的, 若T是单调的且〈y* -x*,y-x〉= 0和(x,x*),(y,y*)∈graphT可推出(x,y*),(y,x*)∈graphT;

3) 在K上强伪单调的, 若存在γ ＞0, 使得对∀(x,x*),(y,y*)∈graphT有:

4) 在K上f-强伪单调的, 若存在γ ＞0, 使得对∀(x,x*),(y,y*)∈graphT有:

5) 在K中的子集B上是Lipschitz连续的, 若存在L ＞0, 使得

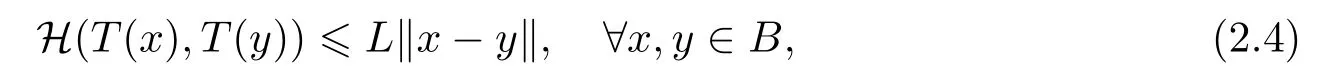
其中H(·,·)是H中的非空有界闭子集的Hausdorff度量, 即

注2.1[14]各种单调性之间蕴含关系如下:

定义2.3[15]对于一个凸函数f:H →(-∞,+∞], 我们用domf={x ∈H:f(x)＜+∞}表示其有效域, 对于给定的点x ∈domf,f在点x的ε-次微分用∂εf(x)来表示, 其中

若ε=0, 则∂f(x)=∂0f(x)表示f在点x的次微分.

定义2.4[16]设K是Hilbert空间H上的非空闭凸子集, 则点z到K的距离定义为

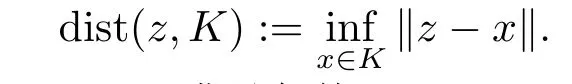
用PK(z)表示点z到K上的投影, 即PK(z)满足条件

引理2.1[16]设K是Hilbert空间H上的非空闭凸子集, 那么有如下性质成立:

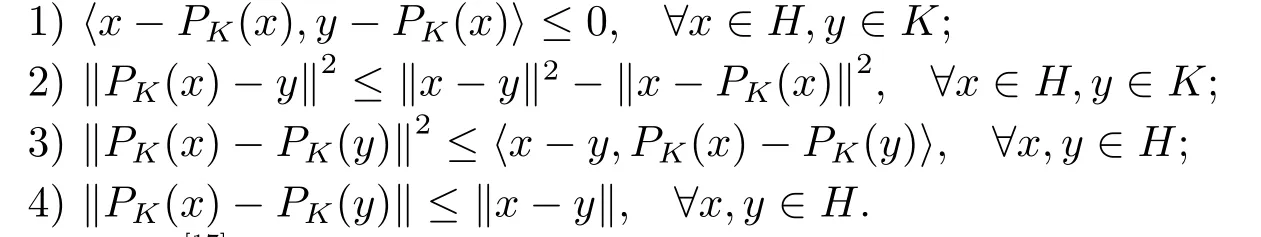
定义2.5[17]一个具有非空弱紧值的集值映射T:K →2H称为H-半连续的, 如果对于∀x,y ∈K, 函数H(T(x+t(y-x)),T(x)) : [0,1]→R+在0+处是连续的, 其中R+= [0,∞),H为Hausdorff度量.

下面的引理是文[17]中引理2.2的特殊情形.

引理2.2[17-18]设f:H →R∪{+∞}是一个真凸下半连续函数,T:K →2H是具有非空弱紧值的H-半连续且单调的集值映射, 则对于x* ∈K, 下面两个式子等价:

3.算法及其收敛性分析

下面将介绍一种求解f-强伪单调或单调集值混合变分不等式问题(1.1)的自适应惯性投影次梯度方法.在我们的研究中, 需要使用下面的条件:

(A1)T是f-强伪单调映射;

(A2)T是具有非空弱紧值H-半连续且单调映射;

(A3)T在有界集上是有界的;

(A4) Sol(T,K)∅;

(A5)f:H →R∪{+∞}是一个真凸下半连续函数且K ⊂int(domf),∂εf在K上是有界.

算法设计如下:

算法A(SMVIP(T,K)的自适应惯性投影次梯度算法)

步0 取初始点x0∈K,v0∈T(x0),θ ∈[0,1), 令k:=0.

步1 若0∈T(xk)+∂f(xk), 则停止; 否则执行步2.

步2 选择αk, 使得其中

计算

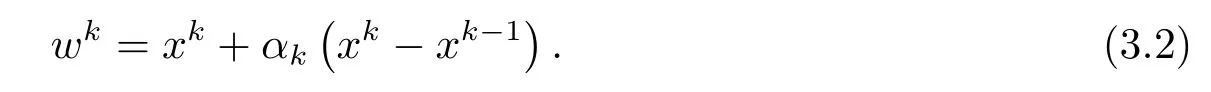
取uk ∈∂εkf(xk),ηk=max{1,‖vk‖+‖uk‖}, 计算

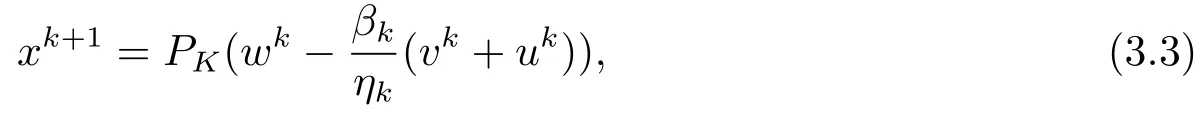
其中

步3 取vk+1∈T(xk+1), 使得

令k=k+1并转回步1.

注3.1若我们取θ= 0, 从而= 0,αk= 0, (3.2)式变成wk=xk, (3.3)式变成xk+1=则此时算法A即为文[5]中的投影次梯度算法.

注3.2若T是单值映射, 则我们可以计算vk+1=T(xk+1), 则步3中的(3.5)式自然成立.

注3.3在步2中(3.2)式采用惯性技术, 将投影方法与步长规则相结合.

引理3.1设序列{xk}是由算法A生成的, 则对∀z ∈K, 有下面的不等式成立:

证由φk的定义有

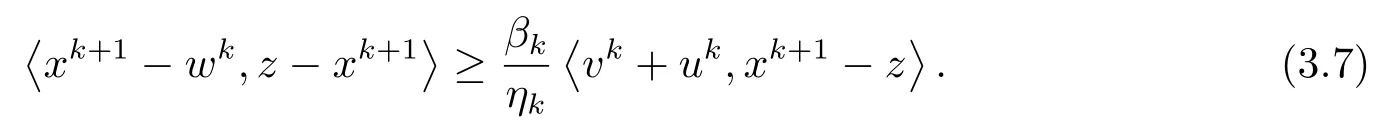
结合(3.6)和(3.7), 我们有

另外

由(3.8)和(3.9)有

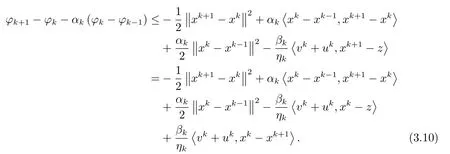
利用Cauchy-Schwarz不等式和均值不等式有

以及

因此, 结合(3.10), (3.11)和(3.12)有

故结论得证.

下面分析由算法A所生成序列{xk}的收敛性.

定理3.1若由算法A所生成的序列{xk}只有有限个元, 则xk是SMVIP(T,K) 的解.

证若序列{xk}只有有限个元, 则对于某个xk, 算法A将在步1处停止.从而, 0∈T(xk)+∂f(xk), 故存在ω ∈T(xk), 使得-ω ∈∂f(xk).由次微分的定义知:

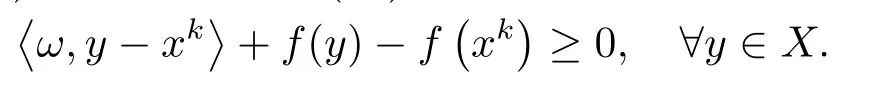
从而,xk是SMVIP(T,K)的解.

下面, 我们假设由算法A所产生的序列{xk}有无穷多个元.

定理3.2假设条件(A1), (A3), (A4)和(A5)成立, 则由算法A生成的序列{xk}强收敛于SMVIP(T,K)的唯一解.

证由假设(A1)知T是f-强伪单调的, 这表明SMVIP(T,K)的解具有唯一性.

事实上, 设x1,x2∈Sol(T,K), 且分别存在ω1∈T(x1),ω2∈T(x2), 使得

和

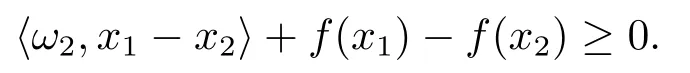
由T的f-强伪单调性可得, 存在γ ＞0, 使得

结合(3.13)和(3.14)可得

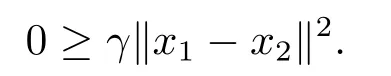
因此x1=x2.

现在设x* ∈Sol(T,K), 由引理3.1可得

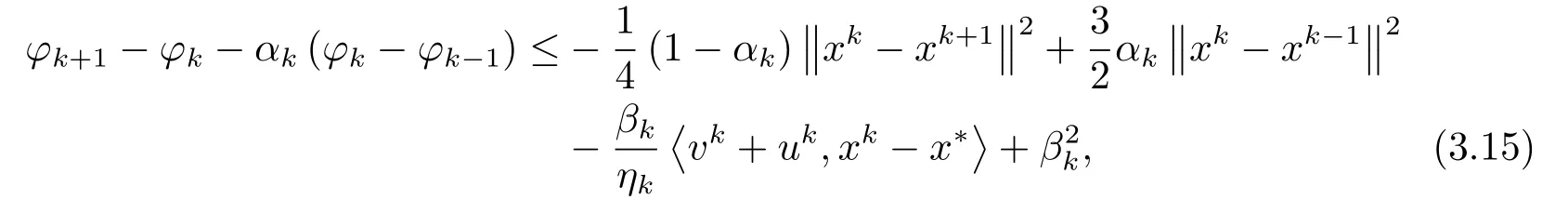
因为uk ∈∂fεk(xk), 则有

从而

将(3.16)代入(3.15)中有

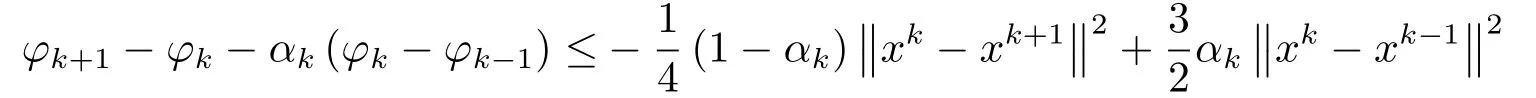
因为x* ∈Sol(T,K), 且存在ω* ∈T(x*), 使得

又由T的f-强伪单调性知, 存在vk ∈T(xk), 使得

从而(3.17)化简得

利用引理2.4, 令

将(3.18)代入(3.19), 再利用φk的定义有

由前面的证明知序列xk有界.设B是包含xk的一个有界集, 且¯ε=sup{εk}.则

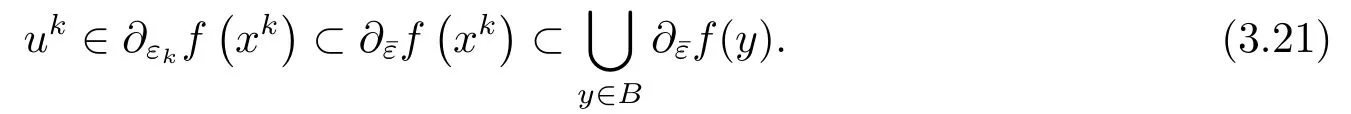
由(3.21)和假设(A3),(A5)知,序列uk和vk都有界,则存在ρ ＞1,使得对所有的k,有≤ρ.从而

则

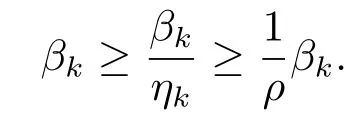
再结合(3.4)得

即{xk}强收敛于SMVIP(T,K)的唯一解.

注3.4与文[11]的算法不同的是, 本文将文[11]针对经典变分不等式问题的算法推广到集值混合变分不等式问题.定理3.2在T为f-强伪单调条件下, 证明了该算法的强收敛性.而文[5]的定理3.5在T是仿单调的情况下证明了算法3.1的弱收敛性.

当算法A中的θ=0时, 我们可以得到如下的算法B.[5]

算法B(SMVIP(T,K)的投影次梯度算法)

步0 取初始点x0∈K,v0∈T(x0),θ ∈[0,1), 令k:=0.

步1 若0∈T(xk)+∂f(xk), 则停止; 否则执行步2.

步2 取uk ∈∂εkf(xk),ηk=max{1,‖vk‖+‖uk‖}, 计算

其中

步3 取vk+1∈T(xk+1), 使得

令k=k+1并转回步1.

接下来我们分析由算法B所生成的序列{xk}的收敛性.

定理3.3假设条件(A2)-(A5)成立,则由算法B所生成的序列{xk}弱收敛于SMVIP(T,K)的一个解.

证当θ=0 时, 则αk==0, 利用引理3.1, 对∀z ∈K, 有

再利用φk的定义有

则

因为uk ∈∂fεk(xk), 则有:〈uk,xk-z〉≥f(xk)-f(z)-εk, ∀z ∈K.

则

从而

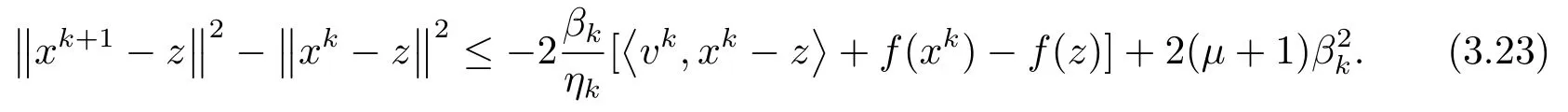
若z ∈Sol(T,K), 且存在ω ∈T(z), 使得

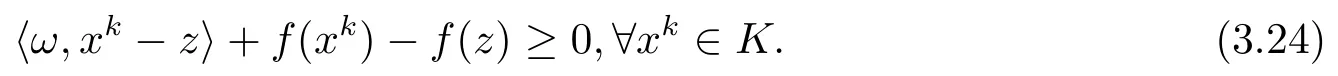
由于T是单调的, 则对ω ∈T(z),vk ∈T(xk)有

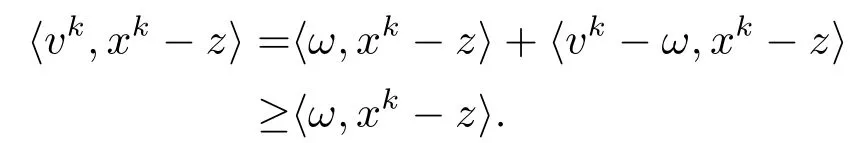
将上式代入(3.23)得

将(3.24)代入(3.25)有

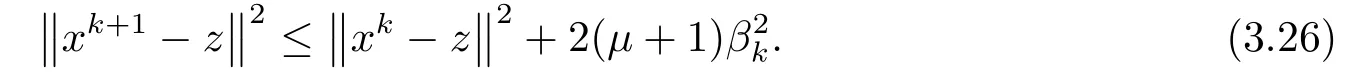
这表明序列{xk}关于Sol(T,K)是quasi-Fejr收敛.由引理2.3中1)知,{xk}有界.

先证明{xk}的所有弱聚点属于Sol(T,K).设是{xk}的弱聚点, 则存在{xk}的子列{xkj},有:xkj ⇀

将(3.25)整理后有

在(3.27)用kj取代k有

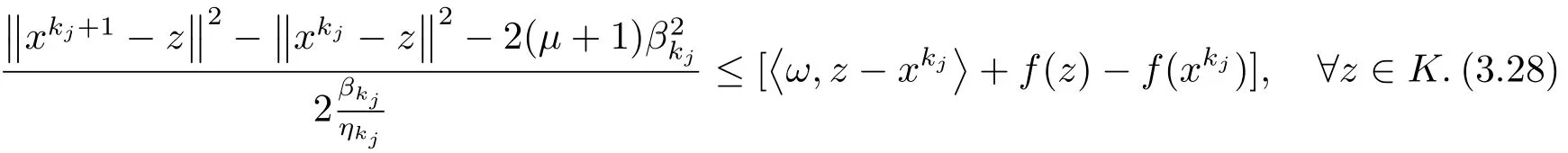
由假设(A2), (A5)和引理2.2知, 上式等价于

注3.5在定理3.3中, 假设条件(A2), (A3)与文[5]的假设(A3)(即:T是具有有界凸值的仿单调映射, 使得T是弱闭且在H的有界子集上是Lipschitz连续)相比,T是不需要Lipschitz连续性, 其中文[14]中的例3说明了我们的假设(A1), (A3)的合理性.

注3.6在定理3.3中,T是单调映射, 文[5]要求T是仿单调映射, 两者的关系见注2.1.

下面我们增加假设条件: Sol(T,K)的内部非空, 可获得{xk}的强收敛性.

定理3.4假设条件(A2)-(A5)成立且int Sol(T,K)∅, 则由算法B生成的序列{xk}强收敛于SMVIP(T,K)的一个解.

证由定理3.3知{xk}有界, 则存在R ＞0, 使得对∀k, 有‖xk‖≤R.定义序列{zk}:

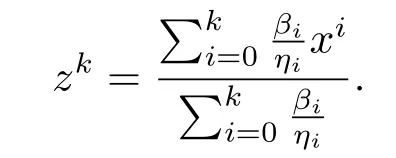
由于f是凸函数, 则有

从而

故化简不等式(3.30)得

上式用kj取代k有

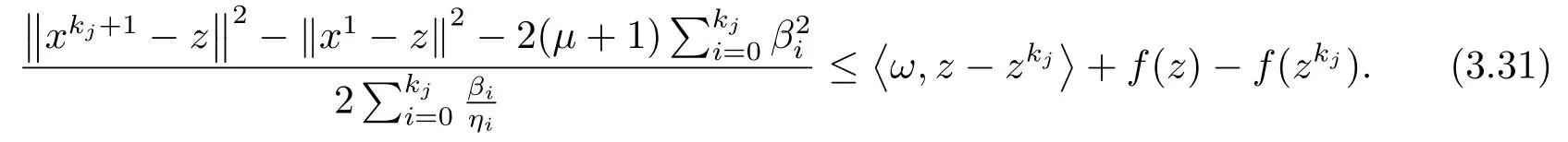
注3.7定理3.4证明了由算法B生成序列的强收敛性, 而文[5]的定理3.5只获得了弱收敛的结果.

4.结论

本文是针对在实Hilbert空间中的集值混合变分不等式问题, 对之前学者提出的投影次梯度算法以及结果进行了适当的改进, 引入一类新的自适应惯性投影次梯度算法, 在合适的假设条件下, 证明了该算法的强收敛性.