基于前馈补偿的振动台粒子群迭代学习控制算法

安 欣， 高 峰， 杨巧玉， 杨学山

(1.中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室，哈尔滨 150080；2.哈尔滨理工大学 测控技术与仪器黑龙江省高校重点实验室，哈尔滨 150080)

电磁式振动台[1]适用于校准速度和加速度传感器[2]，以往校准多用正弦波和冲击波作为信号源，而地震波拾振器专用于地震波采集，用地震波信号校准测震仪器更符合仪器真实工作环境[3]。此外部分测振仪器需要实时处理地震信号，如烈度计、地震紧急处置触发装置，因此，需要用地震波信号完成对此类仪器的检测及校准，从而提高振动台上地震波信号的复现精度。

前馈补偿技术可在一定程度上拓宽振动台系统的频带，改善动态特性，提高台面波形复现精度[4]。前馈补偿技术通常采用构建系统逆模型的方法拓展频带宽度及增加稳定性[5]。系统模型参数辨识常采用如最小二乘法[6]、最小均方差法[7]等方法。文献[8]利用子带自适应辨识液压振动台系统模型，并复现振动台功率谱密度。文献[9]提出自适应陷滤波器在线辨识频率的自适应反馈补偿，消除试件与台面对振动台的影响，提高复现精度。文献[10]提出了一种结合离线补偿器的自适应控制器，通过最小二乘法辨识加速度闭环传递函数并计算离线逆模型补偿器。算法收敛速度快，跟踪精度高。

迭代学习控制(iterative learning control，ILC)是一种不依赖于精确系统模型，仅需要少量信息即可达到很好控制效果的控制方法。由于计算过程不需要太多系统信息，所以在振动台波形复现领域有很大的应用空间。文献[11]针对位移控制的振动台提出了一种基于位移-加速度迭代控制方法，较以往位移迭代控制法收敛速度快。文献[12]针对振动台模型不确定性和外部扰动的干扰，提出自适应重复学习控制算法，在系统中插入学习控制器，可不依赖于具体模型。但在振动台迭代学习控制过程中需要优化控制律参数。控制律参数的好坏直接影响控制算法的收敛速度以及复现精度。

粒子群(particle swarm optimization,PSO)算法在参数优化算法中具有容易实现、收敛速度快等优点。可以为多种算法优化参数，如PID控制[13-14]、模糊控制[15]、神经网络等[16]。孙明翰等[17]在粒子群算法收缩因子中加入扰动因子并仿真了双辊薄带振动铸轧机液压控制系统，提高了收敛速度和求解精度。王闯等[18]提出了鱼群-粒子群算法，引入了拥挤因子和马尔科夫链并将该算法应用于K-means聚类算法中。Xia等[19]改进了粒子群速度项的权重算法，提出了多角色的控制规则，提高粒子群收敛速度。

本文通过前馈逆模型补偿电磁式振动台系统频带宽度，改善系统动态特性，根据实际振动台情况修改逆模型的构造。简化自适应粒子群算法中的速度项目，提高收敛速度，并离线优化带遗忘因子的迭代学习律参数，在减少迭代次数的同时，达到提高波形复现精度的目的。

1 振动台模型

图1为LVC-5型小型电磁式振动台3D示意图，四片弹簧片作为弹性悬挂，稳定台面使其静止在标尺零点。由动圈产生磁场推动台面做水平运动。系统可看成单自由度系统。

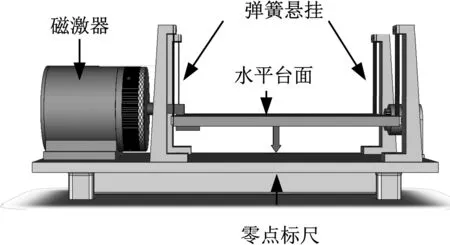
图1 电磁式振动台3D模型Fig.1 3D model of electric shaking table

图2(a)为振动台力学模型，激振器通过电磁感应产生推力F推动振动台做往复运动，k为悬挂弹簧刚度；C为阻尼力系数(忽略空气阻尼)；M为台面和载荷质量；x为台面相对于底座的运动位移；图2(b)中驱动电压为e，通过放大器放大K0倍生成输入信号u加入激振器中。图2(c)为激振器动圈上的等效电路，动圈等效电阻为R0；等效电感为L0；形成感应电动势G0sx。

(a)

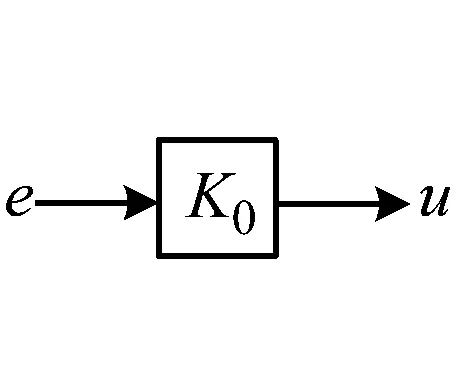
(b)

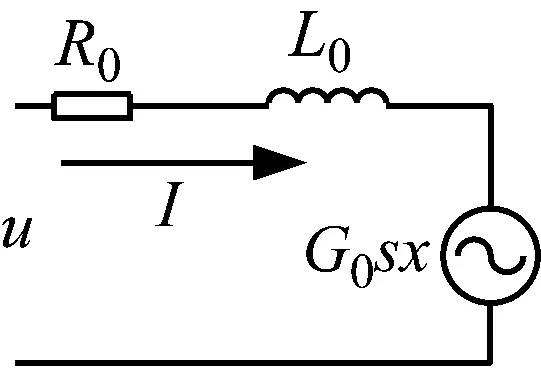
(c)图2 振动台模型Fig.2 Mechanical model

振动台的运动和电气方程可表示成

(1)

图3为振动台的结构框图。

图3 振动台结构框图Fig.3 Structural block diagram of shaking table

设：

(2)

则式(1)可写成

(3)

式(3)为位移对驱动信号的传递函数，而地震波采样信号多取加速度信号，所以将式(3)位移量取两次微分得到式(4)。

(4)

由式(4)可看出，加速度信号增益在n11与nn之间较为平坦。本文所用振动台实际参数如表1所示。

表1 振动台参数

振动台频域分析实际上是求取不同频点输入输出的幅值和相位关系，通过输入如下形式的不同频率简谐波信号

x(t)=Xsinωt=X(ejωt-e-jωt)/2j

(5)

式中:X为信号的幅值;ω为信号角频率。系统传递函数为G(jω)，输入输出关系可表示成

y(t)=X|G(jω)|sin(ωt+argG(jω))

(6)

式中:|G(jω)|表示系统的幅频特性;arg(G(jω))为系统的相频特性;ω=2πf为角频率与频率关系。

根据式(6)实测水平振动台频响特性如表2所示。

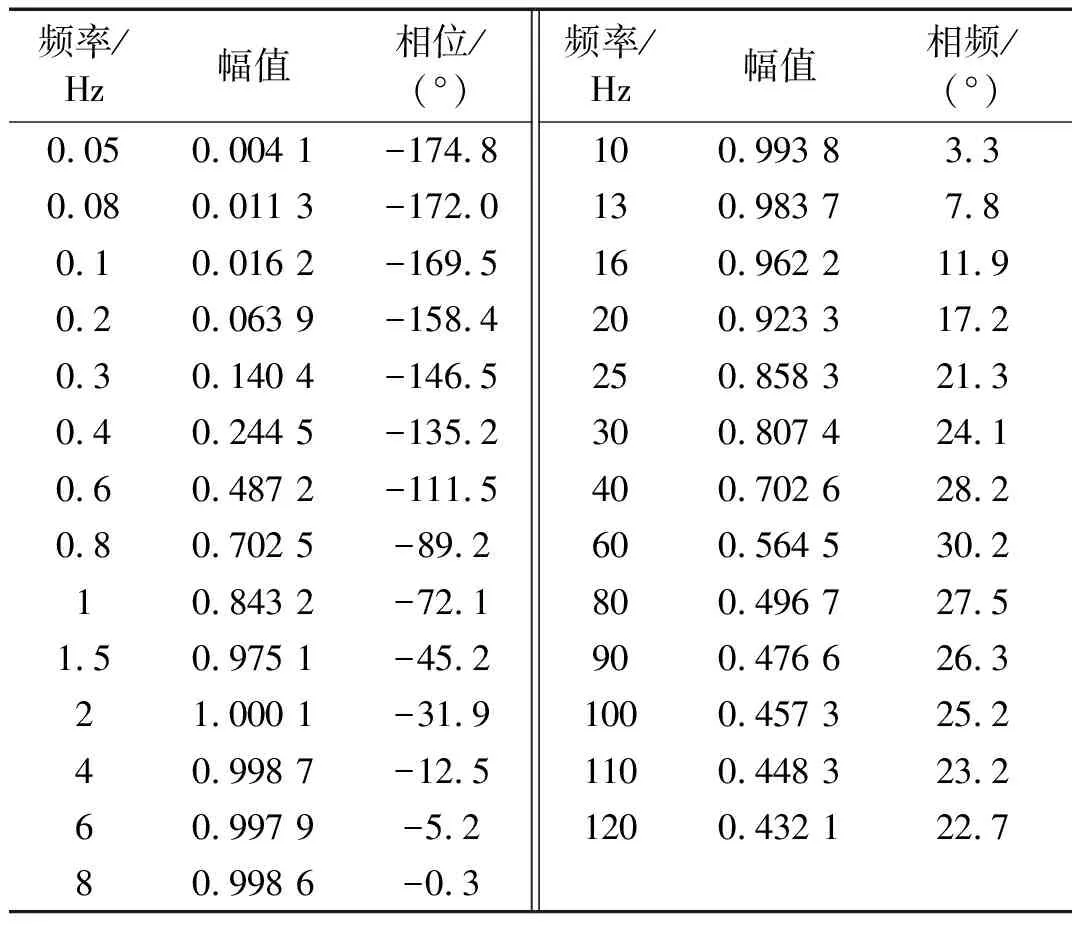
表2 水平振动台频响特性参数

从图4中可看出仿真模型与实测数据在频域中表现基本一致，在1～60 Hz频段内较为平坦。

为验证振动台模型一致性，将振动台实际参数(表1)所示代入式(4)。并与表2中水平振动台实测参数绘制到一张波特图中作对比。

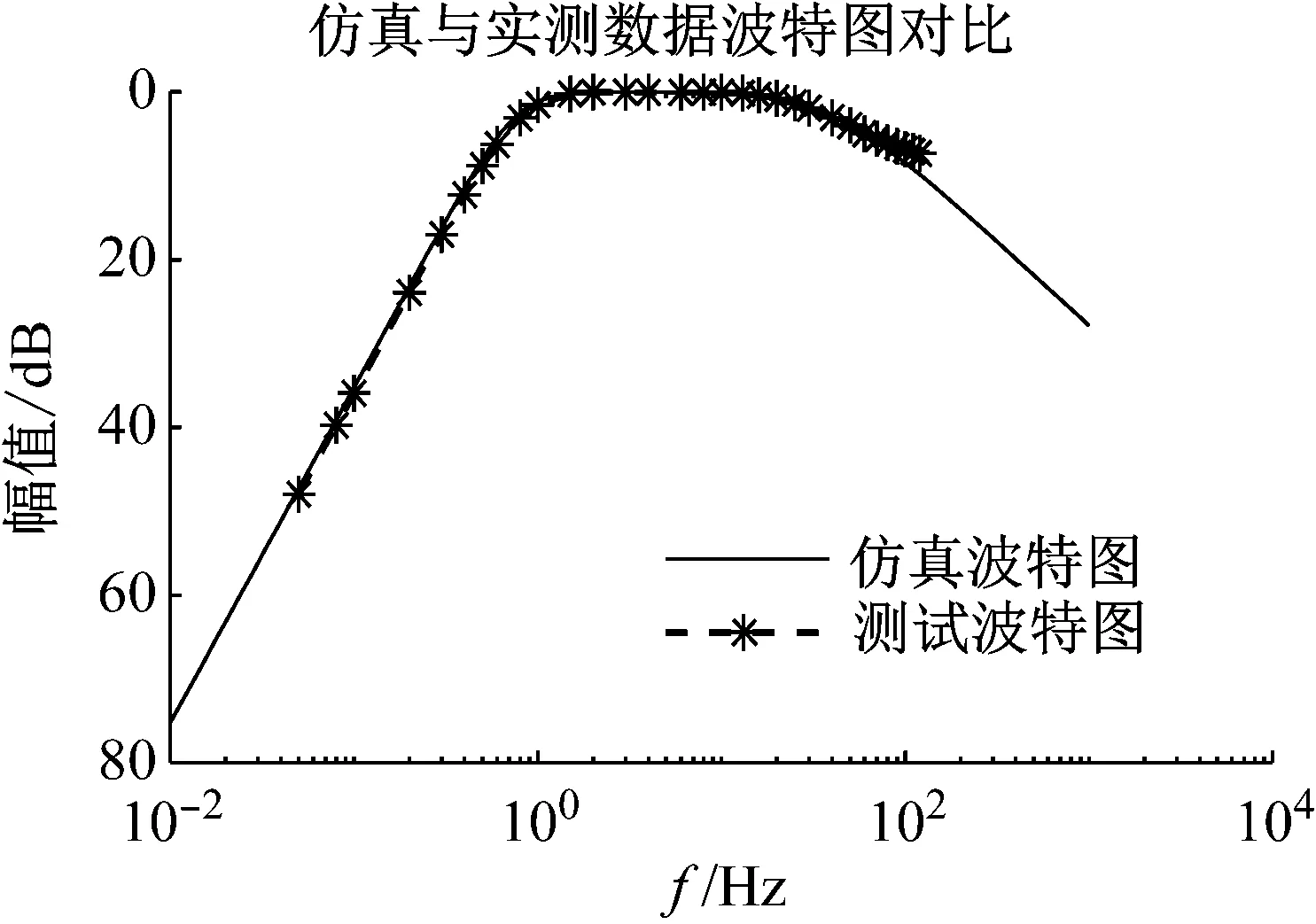
图4 仿真与实测传递函数对比图Fig.4 Comparison between simulation and measurement bode

2 基于加速度模型逆传递函数模型设计

为拓宽振动台频带宽度，提高波形复现效果，在振动台系统前加入前馈补偿器，亦可看作前置滤波器，即构造模型的逆函数

G(s)-1G(s)=1

(7)

式(7)的逆传函在实际构造时需根据情况编辑模型。逆系统对低频信号增益较大，如果驱动信号存在较大的直流分量，将会导致输出信号产生偏移量。而地震波低频成分较丰富，因此需要重新编辑逆模型。首先，对增益较大部分进行平滑衰减，并保证曲线中不存在非线性部分；其次，需要拉平曲线首尾部分，由于后期要拟合并构建逆传递函数曲线，在低频和高频拟合过程中，拟合曲线会沿曲线趋势继续提升，因此，也会造成低频产生较大的增益，最后，通过系统零极点判断系统稳定性。图5为直接通过式(7)得到的逆系统与通过上述方法修正后的逆系统对比图。

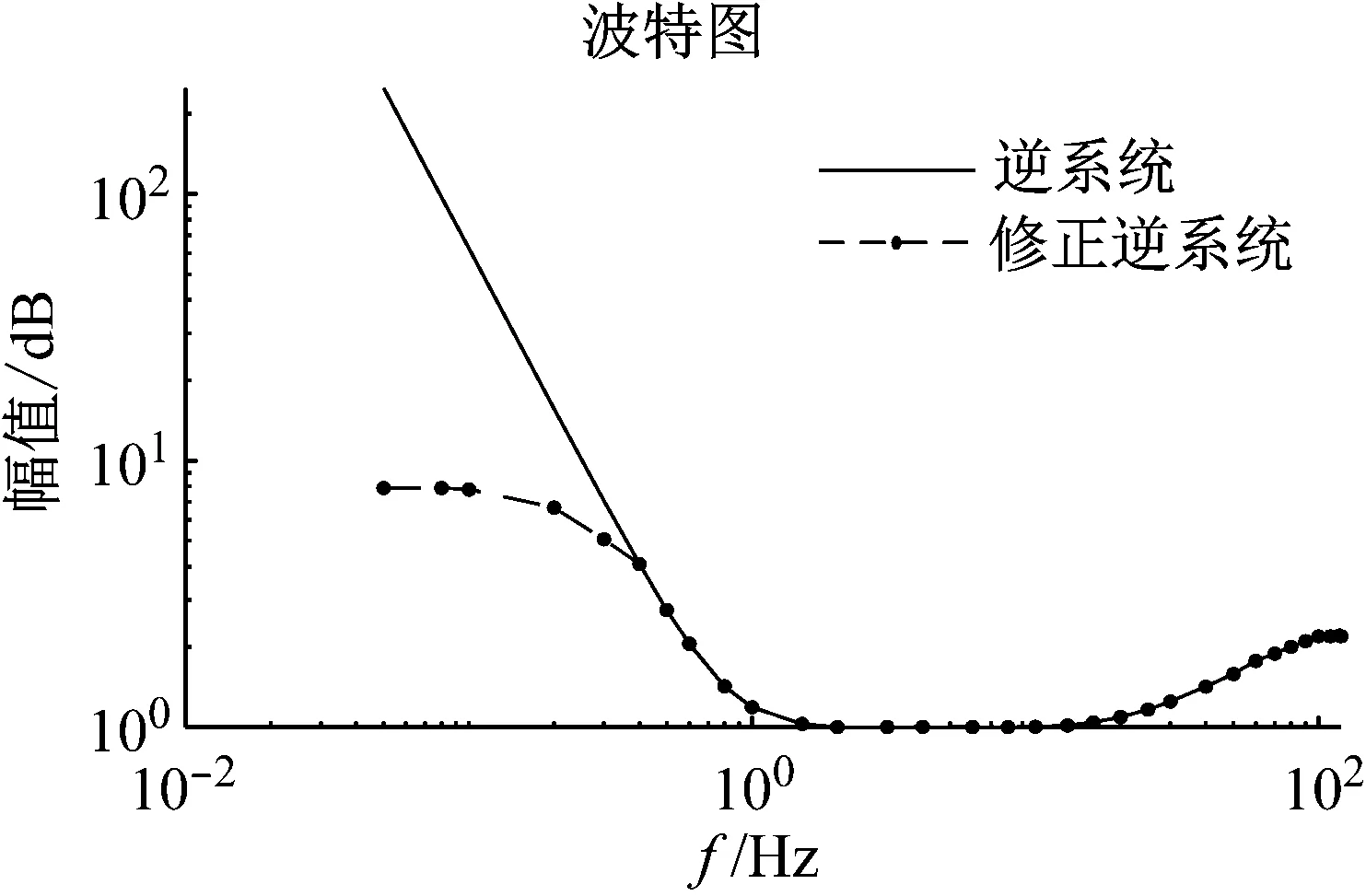
图5 逆函数数据优化Fig.5 Inverse function data optimization

利用Levy法参考图3模型拟合逆传递函数参数

(8)

3 带遗忘因子的反馈辅助PD型迭代学习算法

3.1 系统描述及算法

振动台可近似认为是一种重复运行的线性定常系统，而复现地震波形的目的是要寻找控制输入，使被控系统的实际输出在有限次数重复运行过程中追踪地震波期望信号。电磁式振动台可视为线性定常系统

(9)

式中:系统状态向量xk∈Rn，控制输入uk∈Rr，输出向量yk∈Rm；A∈Rn×n,B∈Rn×r,C∈Rm×n为实数矩阵。假设系统满足(1)期望可达(2)初始状态恒定。

目前地震波复现主要采用迭代控制(iterative learning control, ILC)方法。本文提出一种带遗忘因子的反馈辅助PD型迭代学习算法

(10)

式中:k为迭代次数;r为遗忘因子，r∈[0,1]当系统产生大幅扰动时，遗忘因子可消减扰动对系统的影响;Γ为微分增益系数;L为比例增益系数;yk、uk为系统第k次迭代的驱动信号和输出信号;yd为振动台期望信号;ek为系统实际输出与期望信号的误差。

3.2 收敛性分析

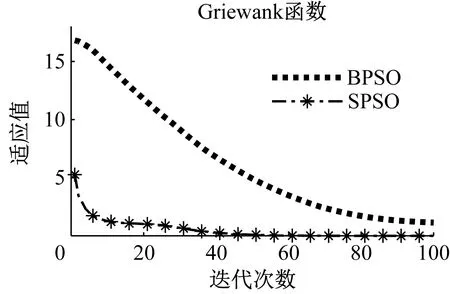
定理 若系统满足

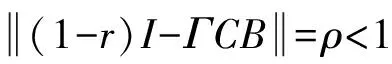
(2) 系统初始不变xk(0)=x0(k=1,2,3…)

证明 式(10)中第k+1次迭代误差可写成

(11)

(12)

求导得

(13)

(14)

上式两端取λ范数

(15)

由Bellman-Gronwall引理和式(9)可得

(16)

对式(16)取λ范数

(17)

式(17)代入式(15)得

(18)

(19)

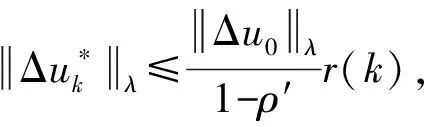
通过上述分析，本文所用的带遗忘因子的反馈辅助PD型学习算法能够跟踪期望轨迹，并且由于引入了上一次迭代和当前迭代的误差信号更新控制输入，形成闭环控制，能保证系统快速收敛。

4 改进粒子群迭代学习(PSO-ILC)算法

4.1 自适应权重粒子群算法

粒子群算法可提前预估学习律模型中的参数。粒子群算法是一种仿生学算法，结合鸟群捕食的策略，通过群体获取的信息更新个体信息。

(20)

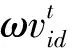
权重信息ω为公式中较重要的参数。惯性权重参数选择过大和过小都不合理，ω过大系统全局搜索能力强，ω过小的话系统局部搜索能力强。所以参数ω调整应该结合自身位置、迭代次数等参数动态调整。设定ω调节范围[ωmin,ωmax]

(21)

式中:f为粒子群的目标函数值；fmin代表粒子群目标函数最小值；favg代表粒子群目标函数平均值。

式(21)中，当粒子群距离比较分散时，即所处位置目标函数值低于平均标准时，减小惯性权重。增强寻找局部最优解的能力，当粒子目标值高于平均值时，则加大惯性权重加速收敛。

4.2 改进粒子群算法

将式(20)更改为如下形式

(22)

(23)

式(23)变换得

(24)

将式(24)整理得

(25)

式(25)说明位置信息迭代式与速度项无关，可化简：

(26)

式(26)由二阶方程化简为一阶方程，计算过程更简单，效率更高。

粒子群算法的适应度函数测试函数有很多，本文选取Griewank、Rastrigin及Schaffer三个函数作测试函数，测试改进粒子群算法的执行效果。

Griewank函数是一个多峰值函数x=0为全局最优解f(x)=0函数有多处局部最小值点。容易陷入局部最优解。考验逃出局部极小值点的能力。表达式为

(27)

x∈[-600,600]

Rastrigrin在x=0有全局最优解f(x)=0函数有多处局部最小值点，峰值较Griewank更多，表达式为

(28)

x∈[-600,600]

Schaffer函数全局最大点在0点处，在距全局最大点3.14的范围内，有无限个局部最大值点。其表达式为

(29)

x∈[-100,100]

图6中改进粒子群算法标记为SPSO，基本PSO算法标记为BPSO。为了增加测试难度，将维度设置为30，迭代次数：100，种群大小为40。对比三种测试函数的适应度迭代曲线，改进粒子群算法寻优速度快，逃离局部极小值效果比未做改进的粒子群算法更快。

4.3 目标函数选取

粒子群算法中的目标函数是算法中个体位置好坏的评价标准。本文粒子群算法需计算迭代学习律中参数，以保证台面复现精度快速提升。所以采用相关系数作为粒子群算法的目标函数，相关系数可评价两个波形相似程度。假设采用X的线性表达式a+bX与Y比较，求得均方误差为

(30)

均方误差可衡量a+bX与Y的相似程度。e越小则两曲线越相似。改变a、b值使e最小即X线性变换后与Y的相似度最高。对e求a、b偏导数并令其等于零

(31)

(a) Griewank测试函数下BPSO与SPSO性能比较

(b) schaffer测试函数下BPSO与SPSO性能比较

设

(32)

将a0，b0代入式(30)得

(33)

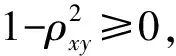
4.4 算法实现流程

首先，通过粒子群算法寻找最优迭代控制律参数r、Γ、L，使迭代波形复现度提升到最高。

如图7所示，PSO算法首先生成随机的r、Γ、L控制率参数、计算出新的驱动函数uk+1并叠加噪声新号。经过式(8)的逆系统后输入给振动台的传递函数，得到振动台仿真输出信号yk与期望信号yd的误差作为迭代学习控制系统的ek，同时计算输出与期望信号的相关系数作为改进PSO算法的适应值。通过PSO不断迭代求得最优rbest、Γbest、Lbest，以减少迭代次数及提高复现精度。然后将最低适应值对应的驱动信号uk代入真实振动台试验中

(34)

经式(34)，进行过少量迭代继续提高复现精度，使相关系数波动不超过0.05为止。

图7 粒子群算法计算最优迭代控制率Fig.7 Calculation of optimal ILC rate by PSO

5 电磁式振动台波形复现实例

2008年汶川地震台网数字记录质量较高，从14个台站42组记录中选取不同的震中距、峰值加速度、频谱分布范围等参数的5组地震波数据作为驱动信号，如表3所示。

表3 地震波记录对比

图8为该5组数据的加速度时域波形及自功率谱密度。

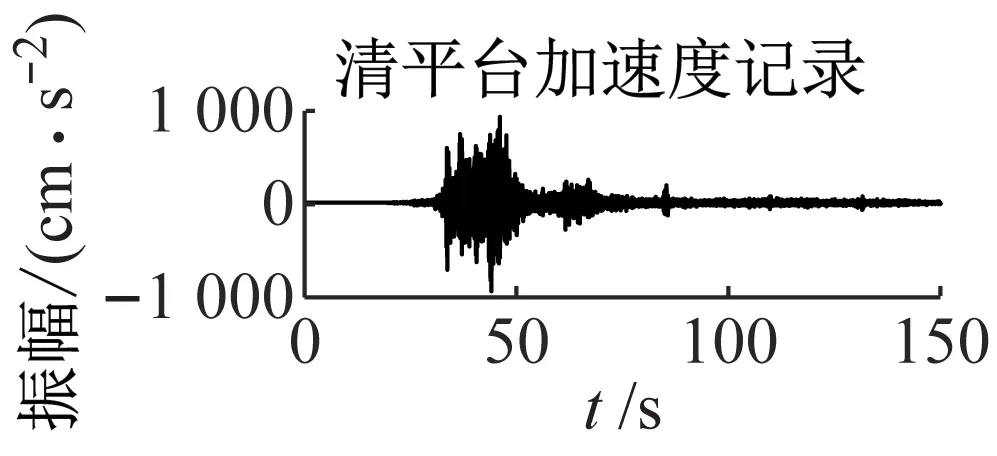
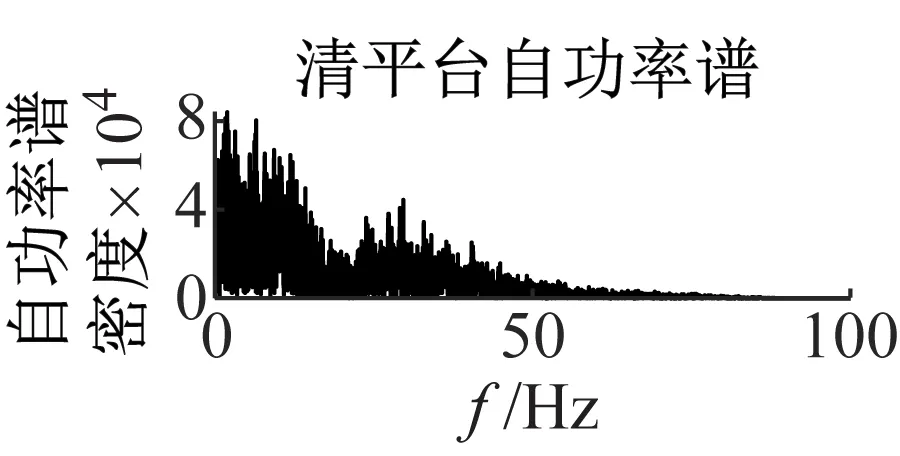
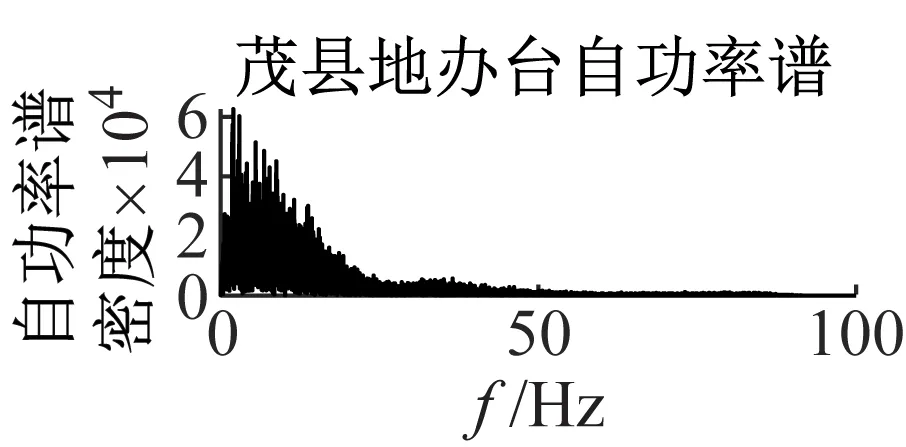
图8 地震波波形及自功率谱Fig.8 Seismic waveform and self-power spectrum

采用式(26)改进粒子群算法，粒子群数为40、c1、c2为2，最大迭代次数为60次，迭代速度控制在[-1,1]区间。驱动波形信噪比设为50 dB。振动台模型根据式(11)和表1中参数设定。迭代结果如图9所示。

图9适应值均收敛到0附近(适应值为0表明复现波形与地震波信号完全一致)。对于以上五种地震波信号，基于改进粒子群迭代学习算法均有效的计算出最优迭代学习控制率参数，能在较少的迭代次数下达到较高的复现精度。

为验证算法结果的有效性，将计算得到参数在图10所示LVC-5型小型振动台中测试。通过NI PXI-6281数采卡发送和采集数据。与文献[12]中方法对比。

表4中数据可以看到，PSO-ILC在迭代次数和复现精度方面均优于同类算法。

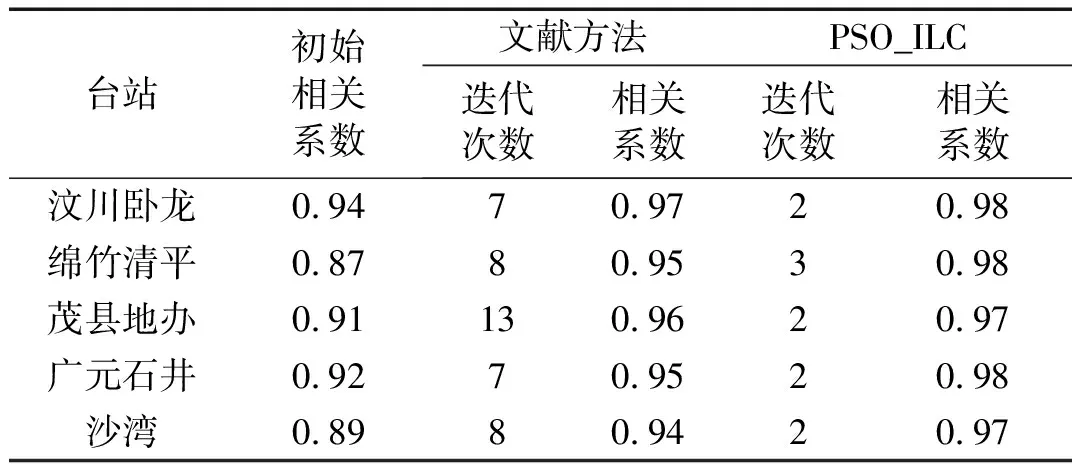
表4 算法对比

(a) 茂县地办：r=0.28,Γ=1.79,L=0.61

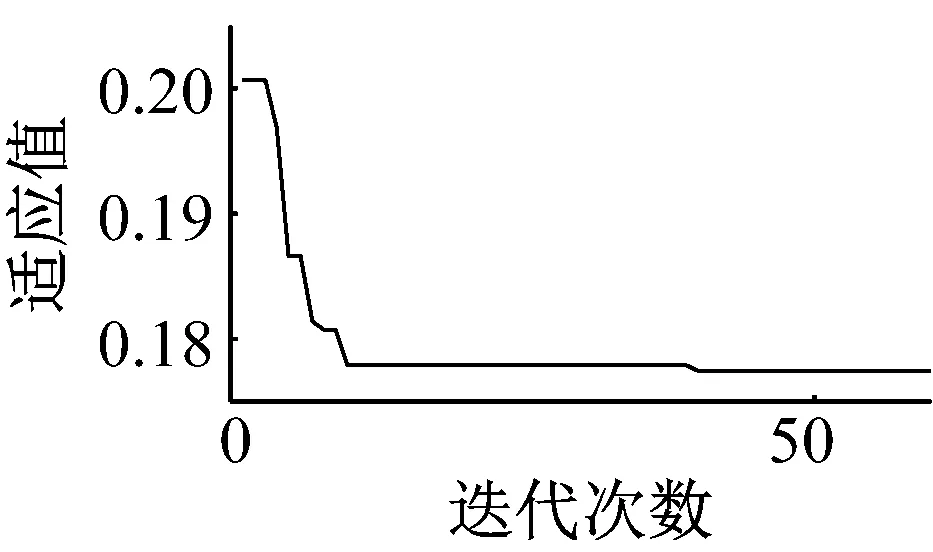
(b) 沙湾：r=0.32,Γ=0.74,L=0.03

(c) 广元石井r=9.32,Γ=1.69,L=0.14

(d) 卧龙：r=0.12,Γ=0.25,L=0.13

(e) 绵竹清平：r=1.49,Γ=0.97,L=0.35图9 粒子群参数优化曲线Fig.9 Particle swarm parameter optimization curve

图10 电磁式振动台Fig.10 Electric shaking table

6 结 论

本文首先建立系统模型，并在模型前加入前馈逆模型，用来改善系统频带宽度，增强系统动态特性。然后提出了带遗忘因子的反馈辅助PD型迭代学习控制算法，并验证了算法的收敛性。遗忘因子可消除扰动对系统的影响，误差迭代效果更平滑。此外，引入反馈辅助利用之前的误差导数及当前的误差信号作为修正项，加快收敛速度的同时解决了当前误差信号求导带来的非因果问题。之后，通过粒子群算法优化迭代控制律中参数，提出了一种简化速度项的粒子群算法，把算法变为一阶方程，通过三个测试函数对比基本粒子群算法，改进算法收敛速度快，逃离局部最优解能力强。最后利用改进粒子群算法优化带遗忘因子的反馈辅助PD型迭代学习律中的三个参数。使迭代过程更快速的收敛，减少迭代次数的同时提高复现精度。

将模型离线计算出的迭代学习律参数用于实际振动台试验中，并对比其他迭代算法。本文所采用的方案具有迭代速度快、复现精度高的特点。