几类特殊图的一般指标集
姬玉荣 , 刘金萌
(1.河南理工大学 数学与信息科学学院, 河南 焦作 454000;2.河南工业和信息化职业学院 基础部, 河南 焦作 454000)
0 引言
令G=(V(G),E(G))为一简单连通图,V(G)和E(G)分别是图G的顶点集和边集。一个顶点标号函数f:V(G)→Z2诱导出一个边标号函数f*:E(G)→Z2,满足f*(v1v2)=f(v1)+f(v2),∀v1v2∈E(G)。 对于每一个i∈Z2,若f(u)=i,则称顶点u为一个i-点。若f*(e)=i,则称边e为一条i-边。令vf(i)=|{v∈V(G):f(v)=i}|,ef*(i)=|{e∈E(G):f*(e)=i}|。如果|vf(1)-vf(0)|≤1,则称标号函数f是友好的。CHARTRAND等在文献[1]中给出了友好指标集的概念,集合FI(G)={|ef*(1)-ef*(0)|:f是友好的}称为图G的友好指标集。关于图的友好指标集,可参阅文献[2-8]。SHIU和LING[9]把友好指标集推广到了全友好指标集。 图G的全友好指标集为FFI(G)={ef*(1)-ef*(0):f是友好的}。若将i-点的集合记作Vi,i∈Z2,那么V0、V1就构成图G的一个二划分。在图的划分理论中,友好标号又被称为平衡划分[10-11],它在并行计算、大规模集成设计等领域有着广泛的应用。从算法[12]的角度来看,确定图友好标号中1边的最大值或最小值是NP困难的。研究者主要集中在一些特定图的研究上。例如,SINHA和KAUR[13]研究了Kn、Cn、Fn、F2,m和P3×Pn的全友好指标集;SHIU和LING[9]确定了两个圈的笛卡尔积的全友好指标集;SHIU和WONG[14]研究了圆柱图的全友好指标集;SHIU和HO[15]确定了一些Petersen图的全友好指标集,并且在文献[16]中确定了细圆柱图和扁圆柱图的全友好指标集。
本文把全友好指标集的概念推广到一般指标集。令G=(V(G),E(G))为一简单连通图,任意一个顶点标号函数f:V(G)→Z2诱导出一个边标号函数f*:E(G)→Z2,其中∀v1v2∈E(G),有f*(v1v2)=f(v1)+f(v2)。
定义图的一般指标集为GI(G)={ef*(1)-ef*(0):|vf(1)-vf(0)|=m},m<|V(G)|。由于ef*(1)-ef*(0)=2ef*(1)-|E(G)|,所以计算GI(G)就只需要求集合
am(G)={ef*(1):|vf(1)-vf(0)|=m,
m<|V(G)|}。
因此GI(G)={2i-|E(G)|:i∈am(G)}。本文给出圈、路和Cn×P2的一般指标集。
在不引起混淆的情况下,把vf(i)和ef*(i)中的下标省略。
引理1G=(V(G),E(G))是简单连通图,令A={e(1)-e(0):v(1)-v(0)=m},B={e(1)-e(0):v(0)-v(1)=m},C={e(1)-e(0):|v(1)-v(0)|=m},则
(1)A=B;
(2)当m≥0时,A=B=C。
证明(1) 对任意的x∈A,存在f1满足vf1(1)-vf1(0)=m使得
令f2(v)=1-f1(v),则
vf2(1)-vf2(0)=vf1(0)-vf1(1)=-m,
由于所有0-点和所有1-点的标号进行了互换,因此0-边和1-边的数目不发生改变,有ef2*(1)-ef2*(0)=x,所以x∈B。同理可得,对任意x∈B,有x∈A,故A=B。
(2)当m≥0时,C=A∪B=A=B,所以A=B=C。证毕。
由引理1知,am(G)={ef*(1):vf(1)-vf(0)=m,0≤m<|V(G)|}。
1 圈的一般指标集
引理2[16](握手引理) 任一图中
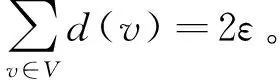
引理3 令f是图G顶点的任意一个0、1标号函数,G中包含一个圈子图Cn,如果Cn中含有一条1-边,那么Cn中的1-边数一定是偶数。
证明把Cn中标i的顶点集合记为Vi,i∈Z2,e(V1)表示V1中所有边的数目,e(V1,V0)表示一个顶点在V1中,另一个顶点在V0中所有边的数目。对于集合V1,运用引理2可以得到,
2|V1|=e(V1,V0)+2e(V1),
所以e(V1,V0)一定是偶数。因此,Cn中的1-边数一定是偶数。证毕。
定理1 GI(Cn)={4-n,8-n,12-n,…,n-2m}。
证明因为0≤m 令v(1)-v(0)=m,由v(1)+v(0)=n,得 因为Cn是2-正则图,所以一个0-点最多只能和2条1-边相邻。因此Cn中的1-边数e(1)≤n-m。 容易计算v(1)-v(0)=m,e(1)=i,i∈{2,4,6,…,n-m}。结合引理3,得到GI(Cn)={4-n,8-n,12-n,…,n-2m}。证毕。 定理2 GI(Pn)= 证明把Pn中的顶点依次记为v1,v2,…,vn。令v(1)-v(0)=m,由v(1)+v(0)=n,得 e(1)≤min{n-m,n-1}。 容易计算v(1)-v(0)=0,e(1)=i,i∈{2,4,6,…,n-2}。 容易计算v(1)-v(0)=0,e(1)=i-1,i∈{2,4,6,…,n}。所以GI(Pn)={{2i-n+1:i=1,2,3,…,n-1,n是偶数,m=0}。 (2)其他情况 容易计算v(1)-v(0)=m,e(1)=i,i∈{2,4,6,…,n-m}。 容易计算v(1)-v(0)=m,e(1)=i-1,i∈{2,4,6,…,n-m}。所以GI(Pn)={2i-n+1:i=1,2,3,…,n-m,其他情况}。综上可以得到,当n是偶数,m=0时,GI(Pn)={2i-n+1:i=1,2,3,…,n-m-1};对于其他情况,则,GI(Pn)={2i-n+1:i=1,2,3,…,n-m}。证毕。 当v(1)-v(0)=m时,记e(i)为em(i),i=0,1。 引理4Cn×P2中1-边数目em(1)的奇偶性与其1-点数v(1)的奇偶性一致。 证明在Cn×P2中,v(1)-v(0)=m,把标i的顶点集合记为Vi,i∈Z2,V1中0-边数记为em(0)。em(1)表示一个顶点在V1中、另一个顶点在V0中所有边的数目,这些边即是Cn×P2中的所有1-边。对于集合V1运用引理2可以得到, 3v(1)=2em(0)+em(1)。 所以em(1)的奇偶性与v(1)的奇偶性一致。证毕。 下面利用标号子图嵌入法,得到Cn×P2的全友好指标集。先给出相关定义。 定义1 图G在友好标号f下,若e(1)=a,则定义该标号图为G(a)。 定义3 将标号图G(a)的两条边uv和u′v′替换为长度为2的路uxv和u′x′v′,并连接x和x′,所得到的新标号图G(b)的过程,称为一个K2-嵌入,记为G(b)=G(a)⊕K2。若顶点u、x、v、u′、x′、v′的标号分别为b1、a1、b2、b3、a2、b4,把这个K2-嵌入记为 定义4 将标号图G(a)的两条边uv和u′v′替换为长度为3的路uxyv和u′x′y′v′,并连接x和x′、y和y′ ,所得到的新标号图G(b)的过程,称为一个C4-嵌入,记为G(b)=G(a)⊕C4。若顶点u、x、y、v、u′、x′、y′、v′的标号分别为b1、a1、a2、b2、b3、a3、a4、b4,把这个C4-嵌入记为 在下面的讨论中,在Cn×P2上所有的K2-嵌入或C4-嵌入都是对于圈上的边uiui+1和vivi+1进行的嵌入,其中i∈{1,…,n}, un+1=u1,vn+1=v1。 为了叙述方便,下面给出一些子结构。 用Ai表示Cn×P2一个标号的C4方格,用e′(1)表示方格插入嵌入后1-边的变化数。 把不同的C4标号记为 把不同的K2标号记为 由上述(1)~(10)的结论得到下面的引理。 引理5 任给i∈{1,2,3,4,5},存在j∈{1,2,3,4},使得e′(Ai⊕Bj)=3。 引理6 任给i∈{2,4,5},存在j∈{1,2,3,4},使得e′(Ai⊕Bj)=1。 引理7[17]当m≥2时,C2n×P2中e0(1)∈{2i:i∈[2,3n]{3n-1}}。C2n+1×P2中e0(1)∈{2i+1:i∈[2,3n]}。 引理8 在C2n×P2中,a2(C2n×P2)={5,7,9,…,6n-9,6n-7,6n-5,6n-3},a4(C2n×P2)={4,6,8,…,6n-8,6n-6},其中am(C2n×P2)={e(1):v(1)-v(0)=m,0≤m<2n}。 证明由引理7知,a0(C2n×P2)={4,6,8,…,6n-6,6n-4,6n},那么在C2(n-1)×P2的友好标号下,a0(C2(n-1)×P2)={4,6,8,…,6n-10,6n-6}。在C2(n-1)×P2的某一个方格中进行一个Bj-嵌入,其中j∈{1,2,3,4}。即嵌入的4个顶点中3个标1-点、1个标0-点。在C2(n-1)×P2的任意友好标号下,必存在A1、A2、A3、A4、A5方格,在Ai中嵌入Bj,由引理5得 {7,9,…,6n-7,6n-3}⊆a2(C2n×P2)。 在C2(n-1)×P2的某个友好标号下,其1-边数为4时,必存在方格A5,嵌入B1,使得e′(A5⊕B1)=1,所以5∈a2(C2n×P2)。在C2(n-1)×P2的某个友好标号下,其1-边数为6n-6时,必存在方格A4,嵌入B2,使得e′(A4⊕B2)=1,所以6n-5∈a2(C2n×P2)。 易知1∉a2(C2n×P2)、3∉a2(C2n×P2)和6n-1∉a2(C2n×P2),结合引理4得,a2(C2n×P2)={5,7,9,…,6n-9,6n-7,6n-5,6n-3}。 因此在C2(n-1)×P2中,a2(C2(n-1)×P2)={5,7,9,…,6n-11,6n-9}。在C2(n-1)×P2的某一个方格中进行一个Bj-嵌入,其中j∈{1,2,3,4}。即嵌入的4个顶点中3个标1-点、1个标0-点。在C2(n-1)×P2中必存在A1、A2、A3、A4、A5方格,在Ai中嵌入Bj,由引理5知, {8,10,…,6n-8,6n-6}⊆a4(C2n×P2)。 在C2(n-1)×P2中满足v(1)-v(0)=2标号下,其1-边数为5时,不可能只存在方格A1和方格A3,所以必存在方格A2或者A4或者A5,嵌入Bj,由引理6得,6∈a4(C2n×P2)。在C2n×P2中满足v(1)-v(0)=4标号下,4∈a4(C2n×P2),2∉a4(C2n×P2)。 结合引理4得,a4(C2n×P2)={4,6,8,…,6n-8,6n-6}。证毕。 定理3 GI(C2n×P2)= 证明1)m≡0(mod 4) 易知1∉am+2(C2n×P2)和3∉am+2(C2n×P2),结合引理4得, am+2(C2n×P2)= 因此在C2(n-1)×P2的顶点标号下,若v(1)-v(0)=m+2,其1-边数目的集合为 am+2(C2(n-1)×P2)= 2)m≡2(mod 4) 类似地,可以得到当m≡2(mod 4)时, 综上可以证得定理结论。证毕。 类似地,还可以得到如下定理。 定理4 GI(C2n+1×P2)= 本文对图的全友好指标集的概念进行了推广,利用嵌入的方法,解决了几类特殊图的一般指标集问题。后续有望对图的一般指标集进行深入研究,得到更一般的构造方法和结论。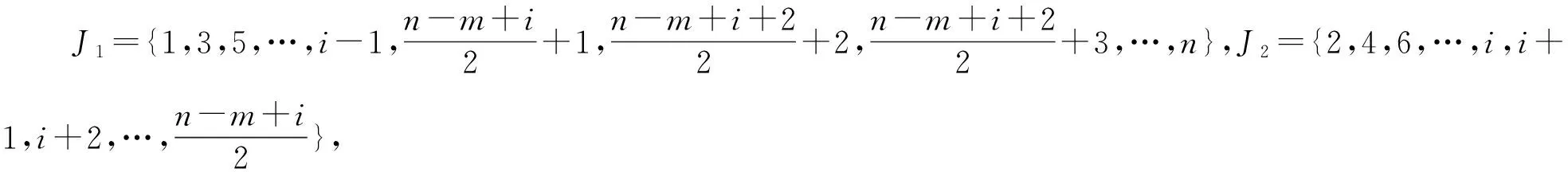
2 路的一般指标集
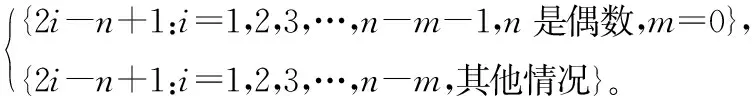
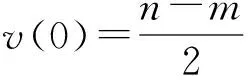
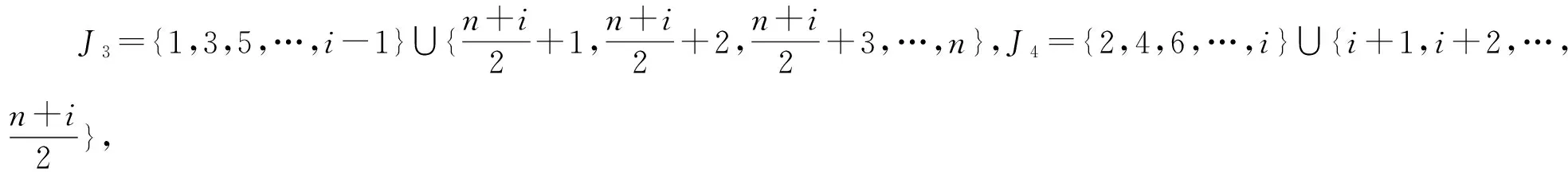
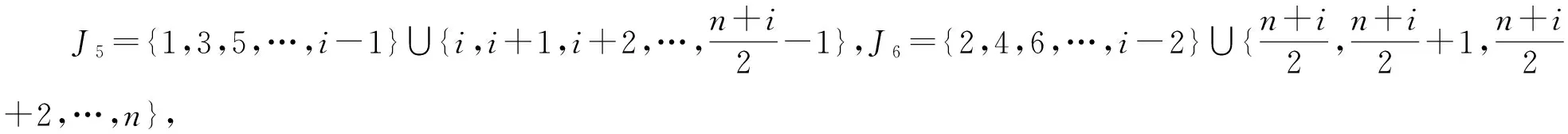
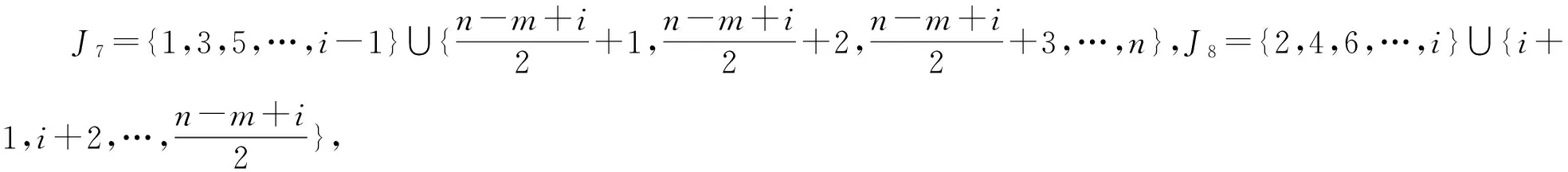
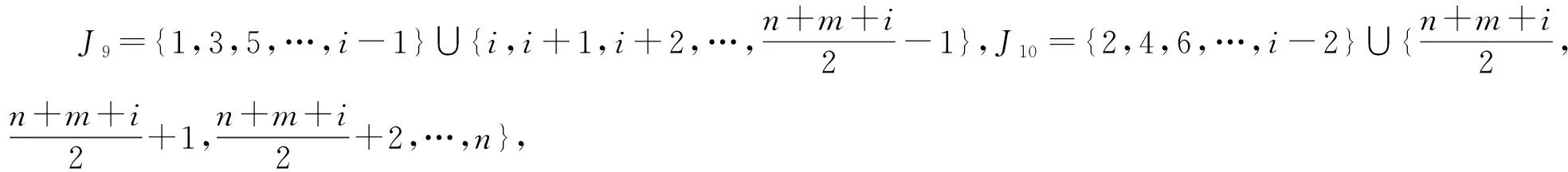
3 Cn×P2的一般指标集
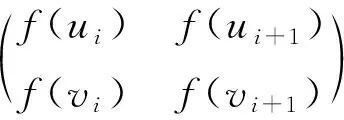
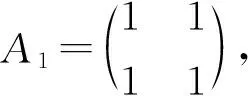
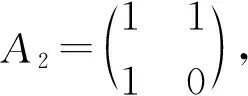
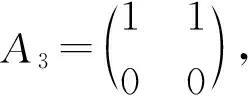
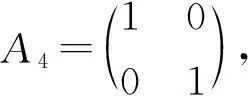
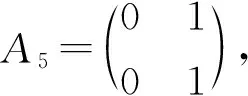
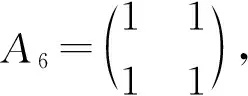
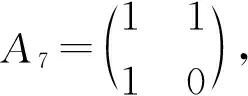
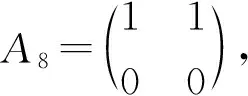
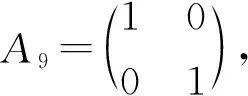
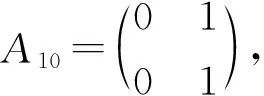
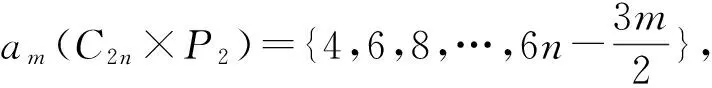
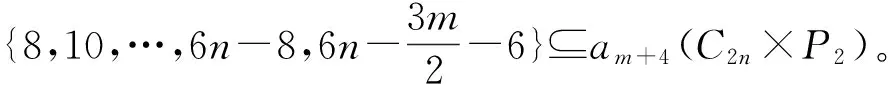
4 结束语

