基于本征正交分解加速的二维位势问题边界元法分析

陈磊磊，胡昊文，李浩挚，赵 娟，袁晓辉

(信阳师范学院 建筑与土木工程学院， 河南 信阳 464000)

0 引言

许多科学与工程领域(如流体力学和结构动力学等)需进行数值模拟或结构优化分析。在模拟优化分析过程中,通常产生高维离散的非线性偏微分方程组，求解这些非线性偏微分方程组往往是极其耗时的，因此，开发出一套高效求解方法是十分迫切的。近年来，一些学者提出模型降阶法，以较小的计算成本获得非线性偏微分方程组的近似解，并成功应用于湍流[1]、结构振动[2]等研究中。

本征正交分解(POD)[3]是一种广泛采用的模型降阶技术，最早由PEARSON[4]提出，也被称为Karhunen-Loeve分解或主成分分析。使用该方法可为给定的一组理论、实验或计算数据提供最优有序、最小二乘意义上的正交基，通过截断这个最优基实现降阶模型或替代模型的目的。另外，该方法在使用过程中，无须与系统数据进行交互，因此具有极强的普适性。考虑到这些优点，DING等[5]采用POD对蒙特卡罗模拟产生的大量样本进行快速计算；LI等[6]采用模型降阶法进行基于等几何边界元的弹性力学结构优化分析，成功实现了高效计算。这些研究都显示本征正交分解(POD)在减少计算量上具有巨大的优势。

边界元法是一种只需在结构表面进行离散的半解析数值方法，相较于有限元法具有降维计算和高计算精度的特点。因此，边界元法受到了许多学者的关注，并成功应用于各个领域[7-9]，包括本文关注的拉普拉斯型边值问题[10]。然而，边界元法也有其固有的缺点，例如形成非对称满系数矩阵，对该满系数矩阵元素的求解与对应的系统方程的求解都是十分耗时的。因此，限制了该方法在大规模实际问题上的应用。一些快速算法被相继提出以克服这一问题，例如快速多极算法、自适应矩阵压缩、快速直接求解法等。

本文在此基础上采用奇异值分解法(SVD)法将位势问题的求解空间分解为几何子空间和设计子空间，采用径向基函数近似设计子空间，最后通过线性组合几何与设计子空间获得随机变量的响应结果，实现了系统信息的压缩表达，并有效地降低了计算量。

1 位势问题的边界元法

位势问题由拉普拉斯方程控制，表达如下：

(1)

其中：u是势函数，2是拉普拉斯算子。对于二维位势问题，即式(1)的基本解u*(x，y)满足下列方程：

(2)

其中：Δi为狄拉克函数，由上式可得到二维位势问题的基本解为：

(3)

其中r表示为场点和原点之间的距离。当源点P在边界Г时，在光滑边界源点P处的边界积分方程为：

(4)

式中：Г为边界，q是势函数的法向导数,q*=∂u*/∂n，n为边界Г的单位外法线方向向量。

假设将边界Г划分为Ne边界单元Гj(j=1,2,…，Ne)，具有Nb个边界节点(本文采用常量元，Nb=Ne)。当源点P位于第i个边界节点上时，方程(4)的离散形式可表示为：

(5)

式中：uj和qj分别表示第j个节点的位势值和通量,Q为场点。

令

(6)

(7)

则式(5)可改写成：

(8)

并令

(9)

(10)

将含有未知量的项全部移动到左端，最终得到如下形式的矩阵方程：

AX=F,

(11)

式中：A为与未知位势u和未知通量q相对应的矩阵C和G中的列元素界组成的Ne×Ne阶方阵，X为由未知位势u和未知通量q组成的Ne阶向量，F为已知位势u和通量q与在系数矩阵C和G中相对应的列元素相乘之后叠加得到的Ne阶已知向量。

2 奇异值分解

位势问题中计算量最大的操作是构建式(11)并寻找式(11)的解。本文采用奇异值分解法(SVD)，通过使用少量样本解，近似得到任一输入变量下的结果响应X。给定一组设计变量αs，其对应的响应为λαs，使用响应λαs构建一个解空间Λ，它可以表示为一组离散数据：

Λ=[λ(α1),λ(α2),…,λ(αm)] =

(12)

式中：Λ∈Rn×m,n的大小取决于响应个数，m的大小取决于取样点的多少。采用SVD分解矩阵Λ，并且选取一组能有效代表解空间的基，可得：

(13)

式中：r=min(m,n)；U∈Rn×n是正交矩阵；uj是ΛΛT的特征向量，也称为Λ左奇异特征向量；V∈Rm×m也是正交矩阵；vj是ΛTΛ的特征向量，也叫作Λ右奇异特征向量；Σ∈Rn×m是一个对角矩阵，对角元素σi按从大到小排列。奇异值分解是非常有用的，因为可以用向量up=span{u1,…,up}(p≪r)描述结构的特征，向量vq=span{σ1v1,…,σqvq}(q≪r)描述设计变量。引入x∈R3表示设计变量，那么U矩阵中的元素uij能够写成：

(14)

同样地，σjvij可写为：

结合专家经验以及相应的技术对各类气象灾害进行定性和定量的分析是建立气象预警机制的重要基础。而资料的积累和相关的技术支持及指标分析有赖于农业、气象等部门的紧密合作。但是，由于我国相关理念和技术出现较晚，缺乏长期的资料和经验累积，导致当前我国的农业气象技术研究的基础信息和数据的不足，难以有效的满足现代农业生产的需求。

(15)

通过这些分解，式(13)可改写为：

(16)

3 径向基函数

设计子空间vq能对系统行为趋势有很好的近似。因此本节采用径向基函数逼近设计子空间。RBF网络是三层前馈网络，类似于Kriging模型。通过引入径向基函数(RBF)，设计函数可近似为：

(17)

其中：m代表取样点个数，ωi是权系数，φi(α)取为高斯核函数，如下表达：

(18)

其中，参数γi将在算例中详细讨论。那么，权系数ωi可以由插值条件φi(α)(i=1,…,m) 求出：

(19)

通过上述操作后，式(16)可改写为：

(20)

任何系统响应都可以通过这种线性组合而不使用完全的边界元法计算来近似。根据这个特点，可以使用一部分取样数据构成矩阵，通过SVD和RBF方法，近似全阶系统响应，避免了使用全阶取样造成的计算量大的问题。奇异值分解组合径向基函数近似，可提高计算效率，减小计算成本。

4 数值算例

4.1 奇异值分解降阶处理

首先确定奇异值分解后Σ矩阵大小的选取。因为在矩阵Σ中，只有对角线上存在元素，每个元素为奇异值，并从大到小排列。大的奇异值包含大的系统信息，所以先测试关于Σ矩阵的阶数选取对原始响应矩阵的影响。生成一个800×1000的矩阵采用奇异值分解，首先Σ矩阵是800×1000的，依次对Σ行列维数做200的降阶，相应的对U和V矩阵做适当地降阶，仍满足原始响应矩阵的维数。选出降阶后矩阵中的40个元素，与原始矩阵对应元素进行对比。

图1 选取不同阶Σ矩阵与原始响应矩阵元素对比Fig. 1 Comparison of elements of different order matrix Σ and original response matrix

图1为降阶Σ矩阵与原始响应矩阵元素对比图。40个元素分别为第一列1～10行编号1～10，第800行1～10列编号11～20，第1行791～800列编号21～30，第800列791～800行编号31～40。从图1中可以看出，奇异值分解方法能够对进行数据降维，减少储存空间，保证精度。但过少的维数如矩阵Σ为400×400，会使数据的精度较差，因此本文在保证降维和精度的前提下，选取Σ矩阵维数为原始响应矩阵行列维数中最小的。

4.2 高斯核函数宽度选择

由于高斯核函数宽度γi对插值效果有很大的影响，文献[11] 对核函数宽度进行了深入研究，表明参数γi依赖于取样个数和数据维数：

(21)

其中：N是数据点的个数，m表示数据维数。下面根据文献[11]的思想对γi进行测试。对于二维位势问题，设积分圆域的半径R∈(0，1)为变参，按0.02等距步长初始取100个原始样本点，每一个样本点的响应为80个边界点位势值。其他参数保持一致，选取20、40、60、80、100组数据(根据公式(21)计算，分别对应γi(i=1,…,5))构成80×20、80×40、80×60、80×80、80×100的矩阵，分别进行SVD、RBF插值计算原始全阶80×100组变量下的结构响应。

为了证明RBF插值的精确度，引入R-squared方法对位势响应的插值结果进行评价：

(22)

其中：n为预测值个数，yi表示解析值，表示RBF的预测值，表示解析值的平均值。评价系数R2的值在0和1之间，表示解析值和近似值之间误差，其值越接近于1，精度越高。整个分解插值过程独立重复5次，RBF波动如表1所示。表1给出了在不同取样个数下，预测值的近似结果与解析解的结果的R-squared评价系数。

表1 不同取样个数下R-squared评价系数Tab. 1 R-squared evaluation coefficient under different sampling numbers

从表1可以看出，不同的插值点个数对应不同的预测点个数,即对应不同的系数γi，当预测个数为0时γi=γ1，即所有插值点与原始样本点重合，说明RBF与解析解拟合得很好，随着预测个数的增多，即原始样本点的减少，评价系数R2逐渐减小，表明插值精度开始降低。但在形状系数为γ4时仍有较高精度，表明使用RBF方法对未知变量响应有着比较精确的预测。总的来说，RBF方法在匹配的系数γi下，能够对结构响应有良好的预测。此外，同一个变量下的不同边界点的响应结果的R2相同，表明每一个变量下的多个响应都有着相同的插值精度。

4.3 降阶快速计算

确定了奇异值分解的矩阵维数选取和径向基函数的宽度公式，接下来结合这两种方法对位势问题的边界元法进行快速计算。假定位势问题的问题域是圆形，半径在1至5范围内按步长为0.5、0.3时选取，随后将边界离散为100个点，内部点取4个。将0.5和0.3步长的原始响应分别构成两个原始响应矩阵。降阶后插值出步长为0.1时边界点和内部点的位势值。

图2是以步长为0.3和0.5时边界点位势值作为原始数据构成响应矩阵，降阶插值0.1步长下的位势值并与解析解进行对比。图3是以步长0.3和0.5时内部点位势值作为原始数据构成响应矩阵，降阶插值0.1步长下的位势值并与解析解进行对比。

图2 不同步长插值结果与解析解对比(以一个边界点为例)Fig.2 Comparison of different step-long interpolation results and analytical solutions (take a boundary point as an example)

图3 不同步长插值结果与解析解对比(以一个内部点为例)Fig.3 Comparison of different step-long interpolation results and analytical solutions (take a interior point as an example)

从图2和图3中可以看出，插值结果跟解析解数据拟合得很好，有很高的收敛性。插值步长越精细，插值结果与解析解的贴合度就更高。这表明上述的降阶插值是行得通的。

表2、表3给出了插值结果和原始数据的数据值，并给出了不同步长与解析解的相对误差。从表2、表3看出，提出的算法与解析解的相对误差在千分位级别，且插值步长为0.3时，相对误差达到万分位级别。所以，插值点越密集，所得到的近似结果越接近真实解，但所需要的计算资源也增多了。综合图表来看，该方法对复杂物理问题的原始模型依赖很小，且巧妙地淡化了边界积分的困难，无论是内部点还是边界点都与解析解的结果高度收敛。总的来说，奇异值分解和径向基函数近似对复杂物理问题的快速计算提供一种新的思路。

表2 不同步长插值结果与解析解的相对误差 (以一个边界点为例)Tab. 2 The relative error between the results of different step-long interpolation and the analysis solutions (take a boundary point as an example)

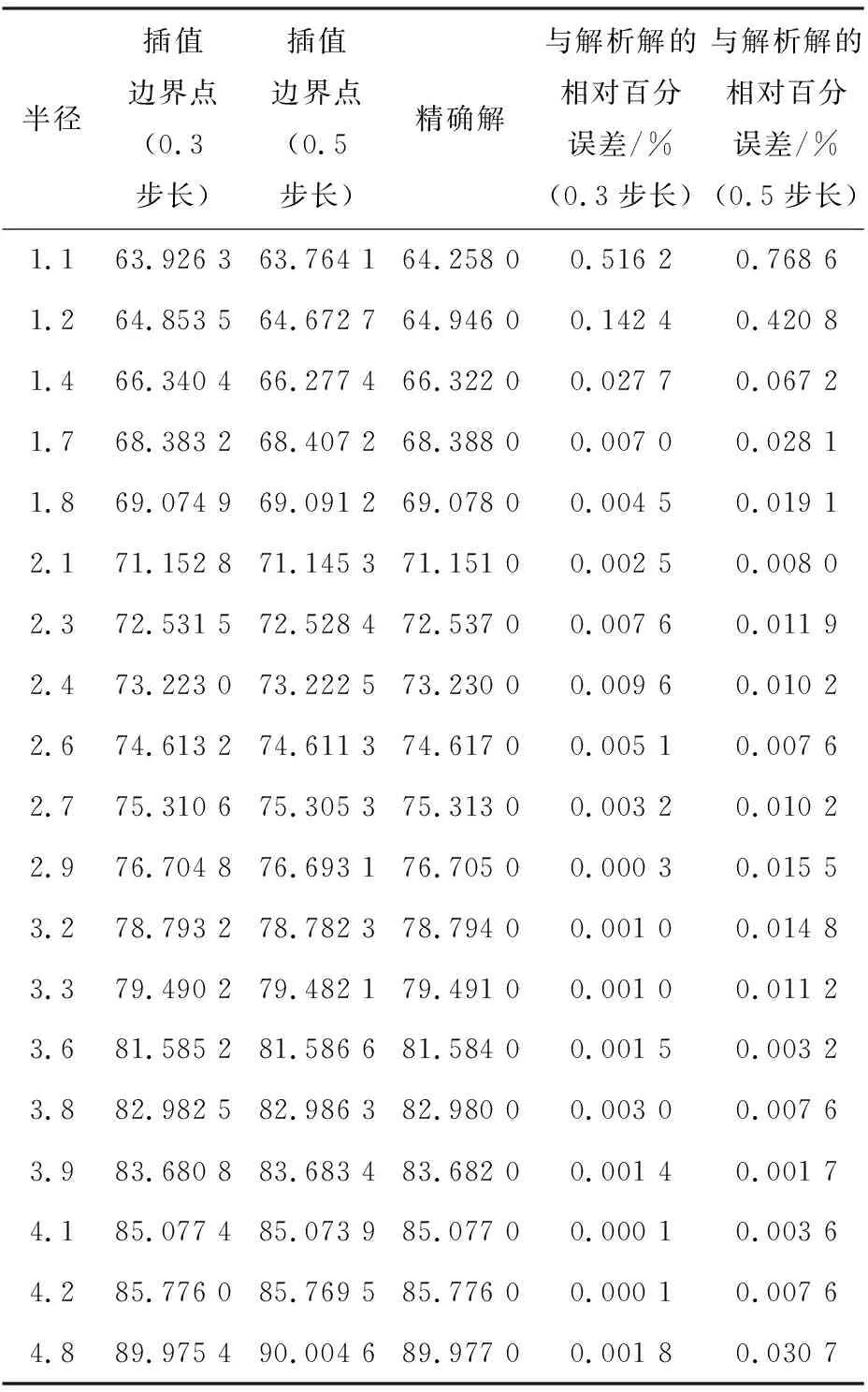
表3 不同步长插值结果与解析的相对误差 (以一个内部点为例)Tab.3 The relative error between the results of different step-long interpolation and the analysis solutions (take a interior point as an example)

5 总结

采用奇异值分解和径向基函数近似快速分析二维位势问题边界元法。测试结果表明，该算法有较好的收敛性，并能够避免复杂的原始迭代过程，从而便捷地获得结果。这一特性降低了计算负担，并且使用小部分数据确保了随机数生成器的准确性。核函数宽度和取样点的选取对精度都有一定的影响，并且插值点越密集，所得到的近似结果越接近真实解。本文讨论了最佳宽度和取样,在最佳宽度下，径向基函数近似结果与解析解有良好的切合;再结合奇异值分解的数据降维，达到快速、高效计算结构响应的效果。这为处理复杂物理问题，提供了一种简单、高效的算法。