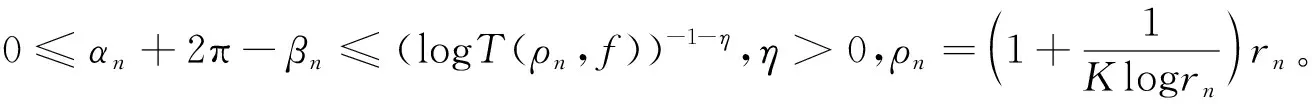双曲区域上的Schottky定理
郑建华,龙见仁
(1.清华大学 数学科学系,北京 100084;2.贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言和主要结果
众所周知,Picard定理、Schottky定理、Landau定理、Montel定理和Nevanlinna第二基本定理、Schwarz-Pick引理(一般的双曲原理)是复分析的几大经典定理,它们引领了复分析的发展和新分支的建立。据我们了解,一般地,Schottky定理的陈述都是在单位圆盘B(0,1)={z:|z|<1}上的。本文的目的是把Schottky定理写到一般的双曲区域(如环域)上。我们将借助双曲度量和万有覆盖来具体实施。同时,由Schottky定理还做出一些延伸,以探索进一步的结论。
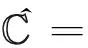
其中,下确界是对所有W内的连接z1和z2的可积曲线γ所取的。下面用λ0,1表示{0,1}的双曲密度。相关细节参看文献[1]。
Schottky定理最佳的界是1979年由Hempel[2]给出的,叙述如下:
设f:B(0,1)→{0,1}是解析函数,那么对∀z∈B(0,1),有
其中等号成立仅当f(B(0,1))={0,1},f(0)是一个负实数且
虽然上式是精确不等式,但由于λ0,1(z)形式复杂,实用性主要体现在理论层面上。因此,具体的精确界是很难确定的。
如下是Schottky定理表达的显式形式之一。
定理A 设f:B(0,1)→{0,1}是解析函数,则对∀z∈B(0,1),有
(1)

为方便,事实上可以把式(1)写成下式
(2)
其中log+被定义为log+x=log max{1,x}。而不等式(2)中没有-log16的不等式是由Hayman[3]于1947年建立的。
下面将使用不等式(2)的形式来陈述结论。
定理1 设W是上的双曲区域,f:W→{0,1}是解析函数,则对任意z0,z1∈W,有
log|f(z)|<(π+log+|f(z0)|)edW(z1,z0)-log16,
(3)
其中dW(z1,z0)是z1和z0在W上的双曲距离。

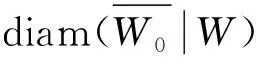

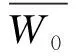
定理2 设W是上的双曲区域,f:W→{0,1}是解析函数,W0是个区域,使得若则∀z∈W0,|f(z)|>1,且z0,z1∈W0,有
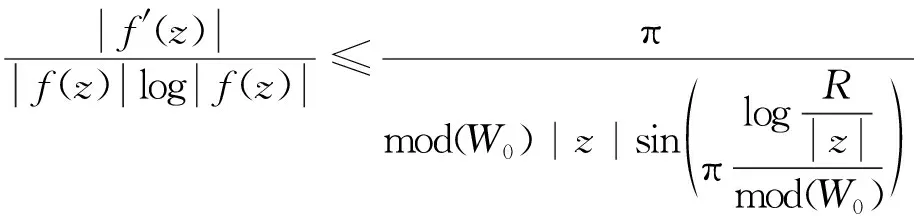
log|f(z1)| 推论1 在定理2的条件下,若W0=A(r,R),则对任意ρ∈(r,R),有 作为上述结论的一个应用,下面讨论超越亚纯函数的增长性。首先引入亚纯函数的Nevanlinna理论中的符号(请参阅文献[4])。设f为亚纯函数,定义 其中n(t,f)表示f在|z| T(r,f)=m(r,f)+N(r,f), 双曲区域W上有双曲度量λw(z)|dz|,其Gauss曲率为-1。单位圆盘B(0,1)上的双曲密度 (4) Ahlfors将Schwarz-Pick引理推到了一般双曲区域上,建立如下结论,称为双曲度量原理:设p是U到V的解析映照,U和V是双曲区域,则 λV(p(z))|p′(z)|≤λU(z),∀z∈U, (5) 其中对某点z0∈U使等式成立当且仅当等式恒成立,且p是U到V的覆盖。 因此,对于U中任意两点z0,z1,有 dV(p(z0),p(z1))≤dU(z0,z1), 也就是两点在解析映照下像间的双曲距离不超过它们原来的双曲距离。这也是解析映照与双曲度量非常奇妙的现象。 根据一致化定理,对双曲区域W,存在万有覆盖映照p:B(0,1)→W,有 (6) 借助式(6),可以推出其他双曲区域上的双曲密度。如,不难推出环域W=A(r,R)={z:r<|z| 定理1的证明选择万有覆盖p:B(0,1)→W,使得p(0)=z0。那么 g=f(p):B(0,1)→{0,1}。由式(2),有 log|f(z1)|=log|g(w1)| =(π+log+|f(z0)|)edB(0,w1)-log16, (7) 其中w1∈p-1(z1)。 因为 dW(z0,z1)=inf{dB(0,w1):∀w1∈p-1(z1)}, 于是从式(7)得到欲证的不等式。定理1证毕。 edW(z,z0)log+|f(z)|>log(16|f(z0)|)-πedW(z,z0) 由此 log+|f(z)|>0,|f(z)|>1, 即 f:W0→D={z:|z|>1}。 由式(5),有 λD(f(z))|f′(z)|≤λW0(z),∀z∈W0。 对于z0,z1∈W0,有 dD(f(z1),f(z0))≤dW0(z1,z0) 又 显然, log|f(z1)|≤edW0(z1,z0)log|f(z0)|。 结合不等式(3),得到欲证的不等式。定理2证毕。 推论1的证明由定理2,得到 f:W0→{w:|w|>1}。 欲证的不等式可以由文献[5]中定理2.4得到,为读者方便,下面给出具体的证明过程。由双曲度量原理式(5),有 (8) 对ρ∈(r,R),可以取到两点z1和z2,使得|z1|=|z2|=ρ,|f(z1)|=M(ρ,f),|f(z2)|=L(ρ,f),记γ为|z|=ρ上z1到z2的最短的圆弧。在γ上,有 上式使用了正弦函数的基本不等式: 沿γ积分式(8)的两边,得 这就得到了欲证的不等式,推论1证毕。 对于An中任意两点z1和z2,由γ表示Wn中连接z1和z2的测地线,有 =6πK(logrn)。 于是diam((An|Wn)<6πK(logrn),从而 ediam((An |Wn ) 1)事实上,在推论2中,可以将An切去一部分,用如下区域来代替Wn,结论依然是成立的。 2)经典的Schottky定理要求考虑的函数不取0,1,∞,但可以尝试考虑适当取到0,1或∞的情况,主要使用Nevanlinna理论来实施,事实表明这样是可行的。例如,1951年Hayman在文[6]上取得了这样的成果。但这个成果要考虑到一般的双曲区域上是困难的,主要困难在于万有覆盖无端添加了额外的取值点。但是单连通区域是可行的。下面展示文[6]中的一个估计,体会一下这方面的结论。 定理B[6]设f(z)=0,1,∞在B(0,1)上至多有L个根,则 其中A是个绝对常数,f*(z)定义如下: 上的所有零点和极点(计重数)。 针对定理B,提出如下问题: 更细致的考虑是否在定理B中可以将f*(z)换成f(z)?这是项有趣的工作。 本文所得到结论同样可以考虑推广到涉及函数可以适当取值的情况,这样推广的结论可以有更广泛的应用,例如,关于正规族的Montel定理的推广。虽然获得这些正规族方面的结论有可能可以从Zalcman引理得到,但从建立的广义Schottky定理直接得到是非常有意义的。 人们也考虑涉及导数的Schottky定理,更进一步的探讨也是具有科学意义的。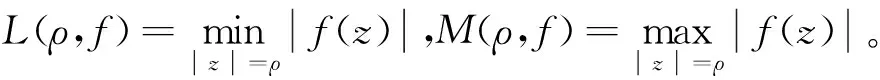
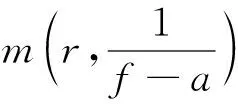
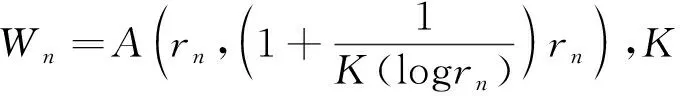
1 结论的证明


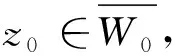
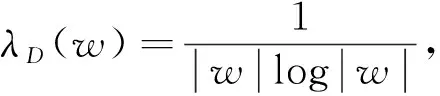


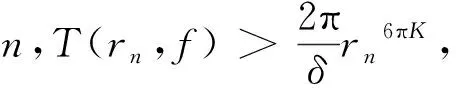

2 讨论