轻量级迭代MDS 矩阵的构造*

王 丽, 陈 媛, 王 石, 曾祥勇

湖北大学 数学与统计学学院 应用数学湖北省重点实验室, 武汉 430062

1 引言

随着信息技术的快速发展, 微型嵌入式设备越来越发达. 由于微型设备在面积、通信能力、计算速度和储存空间等方面有着一定限制, 所以设计更加安全并且轻量的扩散层成为焦点. 与直接使用MDS 矩阵实现最优扩散的扩散层相比, 迭代扩散层有着更小的硬件实现, 因此适用于资源受限环境的迭代MDS 矩阵引起了广泛关注. 迭代MDS 矩阵, 即其本身并不具备MDS 性质, 而将其迭代特定次数后是MDS 矩阵. 更具体地说, 如果At是MDS 矩阵, 则可以通过A而不是At来实现MDS 性质, 但是这种方法往往需要增加t时钟周期, 因此在使用的过程中会有更高的延迟.

矩阵的异或数是衡量线性层实现的另一个重要指标, 异或数越小意味着矩阵的实现代价越低. 而矩阵中非零元的个数越小, 获得较小异或数的可能性越大. 文献[1] 给出了迭代MDS 矩阵的非零元数目的下界和达到该下界时迭代次数的下界, 这使得搜索异或数低且延迟低的迭代MDS 矩阵更加容易. 文献[2]提出一类具有特殊结构的稀疏DSI 矩阵来构造迭代型MDS 矩阵, 该类矩阵的固定异或数仅是友矩阵固定异或数的一半, 在迭代实现中比友矩阵构造的扩散矩阵更轻; 而且对于4 阶矩阵, 稀疏DSI 矩阵可以实现最低的固定成本, 这意味着不存在其他迭代型的MDS 矩阵结构轻于稀疏DSI 结构. 但由于搜索空间过大, 并没有得到8 阶的稀疏DSI 矩阵. 随后文献[3] 证明了F28上的8 阶稀疏DSI 矩阵是不存在的.

关于迭代MDS 矩阵的构造, 在过去的工作中, 迭代次数一般都大于等于矩阵的阶数[1–7]. 在迭代次数等于阶数的情况下, 文献[5,8] 利用友矩阵, 在有限域F24和F28上得到非零元个数为7, 异或数最低分别为15 和33 的4 阶迭代MDS 矩阵. 文献[9] 中构造出了有限域F24上非零元个数为7, 异或数为13的4 阶迭代MDS 矩阵, 但此时矩阵要迭代8 次才能实现最优扩散. 2018 年提出的稀疏DSI 矩阵, 也是在迭代次数等于阶数的情况下构造迭代MDS 矩阵, 在F24和F28上分别得到非零元个数为6, 异或数最低分别为10 和22 的4 阶迭代MDS 矩阵[2].

为减少因时钟周期增加而产生的延迟, 本文研究了迭代次数小于等于阶数时4 阶迭代MDS 矩阵的构造. 在迭代次数分别为2、3、4 时, 证明了4 阶迭代MDS 矩阵所含非零元个数的下界, 并通过矩阵的置换相似分类和MDS 条件, 实现了非零元个数达到下界的4 阶迭代MDS 矩阵的穷搜. 在迭代次数为3 时,我们在F24上找到了非零元个数达到最小值7, 异或数为15 的4 阶迭代MDS 矩阵, 这是迭代次数为3时, 4 阶迭代MDS 矩阵异或数所能达到的最小值; 而在F28上, 我们得到了非零元个数达到最小值7, 异或数为30 的4 阶迭代MDS 矩阵, 不仅实现了迭代次数的降低, 同时有着更低的异或数. 在迭代次数等于4 时, 在F24和F28上我们得到了同文献[2] 中稀疏DSI 矩阵具有相同异或数的一般类型轻量4 阶迭代MDS 矩阵, 其非零元个数达到最小值为6, 异或数分别达到最小值为10 和22.

2 预备知识

本节主要介绍迭代MDS 矩阵相关定义、性质和度量. 首先给出本文中常用的符号, 见表1.

表1 符号说明Table 1 Notations

2.1 迭代MDS 矩阵及MDS 条件

定义1[10]设M ∈Mn(F2m). 若矩阵M的分支数

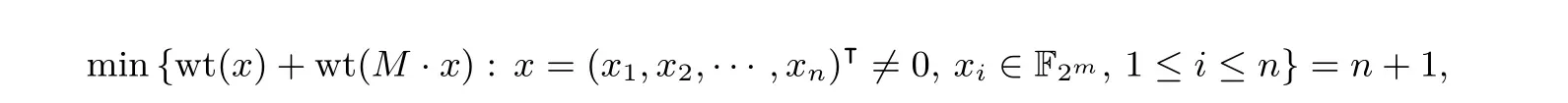
则称M为MDS 矩阵.

注1M为MDS 矩阵当且仅当M的任意阶子方阵都是可逆的[11]. 这个等价条件常用来判断一个矩阵是否是MDS 矩阵.

矩阵分支数是度量矩阵扩散能力的重要标准. MDS 矩阵是矩阵分支数达到上界的矩阵, 它可以有效抵抗差分攻击和线性攻击, 同时提供最优的扩散能力, 这在密码应用中得到广泛应用. 但是因为MDS 矩阵不含有零元, 且大多数元素互不相等, 在资源受限的环境下实现MDS 矩阵很困难. 因此在此基础上, 提出了更适合轻量级应用的迭代MDS 矩阵.

定义2[12]设M ∈Mn(F2m). 若存在正整数t, 使得Mt为MDS 矩阵, 则称矩阵M为迭代MDS矩阵, 称Mt为迭代型MDS 矩阵, 其中正整数t称为迭代次数.

显然, MDS 矩阵是满秩矩阵, 从而迭代MDS 矩阵也是满秩阵, 其每行每列至少含有一个非零元. 因此本文只考虑形如P(D+B′)=PD+B形式的矩阵, 其中P是置换矩阵(即每行和每列有且仅有一个元素为1 而其余元素都为0 的矩阵),D是非奇异对角阵,B′是在非对角位置包含k(k ≥1) 个非零元的矩阵, 即B包含k个非零元且非零元位置与P均不相同. 称能被写成PD+B形式的矩阵为k-XOR 矩阵[3].

例1 3-XOR 矩阵的例子:

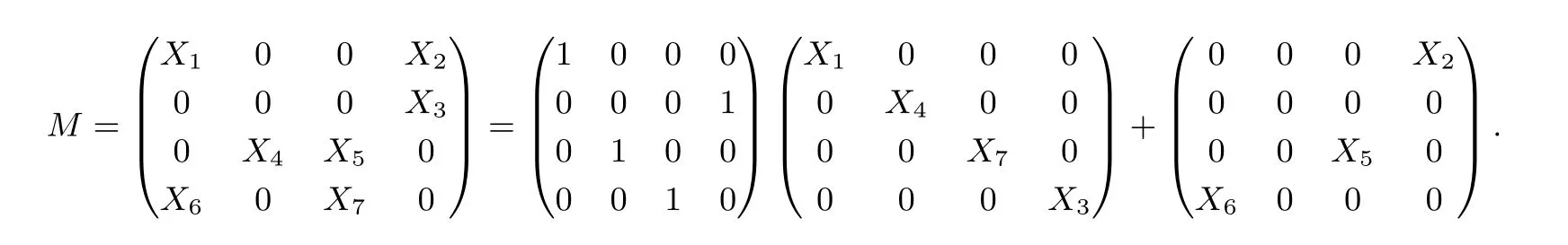
如果有x=(a,b,c,d)⊺, 那么Mx=(X1a+X2d,X3d,X4b+X5c,X1a+X7c)⊺.Mx中的加法总数等于B的非零元个数. 在特征为2 的域中, 这些加法是通过异或来实现的, 因此形如PD+B的矩阵被称为k-XOR 矩阵, 这些异或被称为固定异或数或固定成本. 若M ∈Mn(F2m), 则θ(B) =θ(M)-n=k.M的固定成本为m·k. 非零元素的个数k越小, 越容易构造出实现代价较低的矩阵.

下面我们引入(k,t) 迭代MDS 矩阵的概念.

定义3 设M ∈Mn(F2m). 如果M是k-XOR 矩阵且Mt是MDS 矩阵(t为正整数), 则称M是(k,t) 迭代MDS 矩阵.

注2M ∈Mn(F2m) 是(k,t) 迭代MDS 矩阵当且仅当M⊺是(k,t) 迭代MDS 矩阵.

设M=PD+B ∈Mn(F2m) 是k-XOR 矩阵, 则θ(M) =k+n, 非零元分别用X1,X2,··· ,Xk+n表示. 若M是(k,t) 迭代MDS 矩阵, 则矩阵Mt的元素Mtij(1≤i,j ≤n) 是关于X1,X2,··· ,Xk+n的多项式. 判断M迭代t次后的矩阵是否为一个MDS 矩阵, 我们需要判断矩阵Mt所有的子方阵是否可逆, 即判断所有子方阵的行列式是否为零. 下面给出检查矩阵是否为MDS 矩阵的一种算法[13].

MDS 条件[13]设A为Mn(F2m) 中的非零矩阵,A中所有非零元分别用F2上未定元表示. 则A的子方阵的行列式是一系列F2上关于这些未定元的多项式. 将这些多项式分解为若干个不可约多项式, 则A的每个子方阵都唯一对应一个不可约多项式的集合(若这些多项式中包含零多项式, 则将零多项式加入到此不可约多项式的集合中). 将A的所有子方阵对应的不可约多项式集合并起来得到的集合记为T, 称T为矩阵A的MDS 条件.A是MDS 矩阵当且仅当A中非零元在F2m中的取值, 使得集合T中任意不可约多项式不等于零.

注意到,T中可能会包含零多项式, 这样的矩阵一定不是MDS 矩阵. 为了方便判断, 我们引入MDS条件多项式的概念.

定义4 记集合T中所有元素相乘得到的多项式为fA, 称fA为矩阵A的MDS 条件多项式.

显然, 矩阵A是MDS 矩阵,A的MDS 条件多项式fA必为非零多项式. 即只有当A的MDS 条件多项式不为零多项式时, 它才有可能构成MDS 矩阵.

引理1A为MDS 矩阵当且仅当A中非零元的取值使得MDS 条件多项式fA不等于零.

注3 设M ∈Mn(F2m) 是k-XOR 矩阵. 则M是(k,t) 迭代MDS 矩阵, 当且仅当Mt的MDS 条件多项式fMt在M的非零元取值下的值fMt(m1,m2,··· ,mk+n)/=0, 其中m1,m2,··· ,mk+n分别表示M的非零元.

例2 设M ∈M3(F2m) 是3-XOR 矩阵,X1,X2,··· ,X6分别表示M的非零元,

从而

矩阵M2的MDS 条件为

为(3,2) 迭代MDS 矩阵.

2.2 矩阵及元素的异或数

定义5[8]设M ∈Mm(F2) 是非奇异矩阵. 矩阵M的异或数定义为M非零元的个数减去矩阵维数m, 记为XOR(M), 即XOR(M)=θ(M)-m.

设p(X) 为F2上次数为m的不可约多项式, 则F2m～= F2[X]/(p(X)). 有限域F2m上的任意元素α都可以表示为F2上次数小于m的多项式, 记为fα(X). 令p(X) 的友矩阵为A, 则有限域F2m上的任意元素α都对应F2上一个m阶矩阵fα(A), 这建立了F2m到Mm(F2) 上的一一对应.

定义6[15]设α为有限域F2[X]/(p(X))上的元素.α的异或数定义为实现α与域上任意元素β相乘所需的异或操作数, 记为XOR(α).

有限域上元素的异或数可以通过其对应的矩阵来度量, 即XOR(α)=XOR(Mα).

例3 令α=X+1∈F2[X]/(X4+X+1),β=b3X3+b2X2+b1X+b0是F2[x]/(X4+X+1)上任意元,bi ∈F2. 则

其中符号“⊕” 表示比特异或, 观察可知XOR(α)=5.α·β表示为矩阵乘法也可以写为:

注意到p(X)=X4+X+1 的友矩阵A为

从而α=X+1 对应的矩阵为A+I=Mα. 显然XOR(Mα)=θ(Mα)-4=9-4=5=XOR(α).

对于有限域F2m上n阶非奇异矩阵M的异或数, 则是通过将有限域F2m上的每个元素用其对应的F2上的矩阵替换, 从而得到一个F2上的mn阶矩阵, 设为Mmn.M ∈Mn(F2m) 的异或数即定义为Mmn ∈Mmn(F2) 的异或数. 因此有

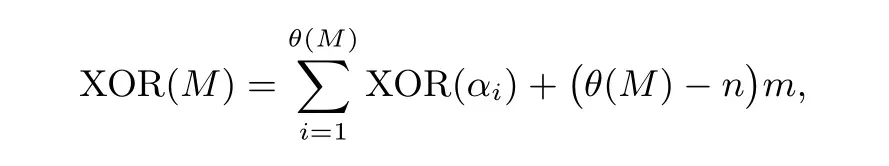
其中αi(1≤i ≤k) 表示矩阵M的非零元.

2.3 置换矩阵及置换相似

本文还需用到置换矩阵的相关性质和置换相似的概念及其性质. 置换矩阵即每行和每列有且仅有一个元素为1 而其余元素都为0 的矩阵. 显然, 置换矩阵与矩阵相乘, 仅改变矩阵元素的行列位置, 不改变矩阵元素的数值. 因此, 置换矩阵的乘积也为置换矩阵.

引理2 令矩阵P, D ∈Mn(F2m) 且P是置换矩阵,D是非奇异对角矩阵. 则对任意矩阵A, 有θ(A)=θ(AP)=θ(PA)=θ(AD)=θ(DA).

证明:P为置换矩阵, 显然有θ(A) =θ(AP) =θ(PA). 又D是非奇异对角矩阵, 令M=AD,有Mij=AijDjj(1≤i,j ≤n), 则Mij/= 0 当且仅当Aij/= 0, 从而θ(A) =θ(AD). 同理可证,θ(A)=θ(DA).

定义7 设矩阵A, B ∈Mn(F2m). 如果存在置换矩阵P, 使得B=P-1AP, 则称矩阵A和B是置换相似的.

显然, 置换相似是矩阵上的一种等价关系.

引理4 设A, B ∈Mn(F2m) 是置换相似的. 则

(1)A是迭代MDS 矩阵当且仅当B是迭代MDS 矩阵, 且迭代次数相同;

(2)A是对角矩阵当且仅当B是对角矩阵;

(3) XOR(A)=XOR(B).

证明: (1) 置换矩阵P与矩阵相乘, 仅改变矩阵元素的行列位置, 不改变矩阵元素的数值, 从而置换相似显然保持矩阵的MDS 性质. 设A=P-1BP, 其中P是置换矩阵.A是迭代MDS 矩阵当且仅当存在正整数t, 使得At是MDS 矩阵. 而At=(P-1BP)t=P-1BtP是MDS 矩阵当且仅当Bt是MDS矩阵.

为一个对角矩阵. 反之亦然.

(3)A, B置换相似, 则它们有着相同的非零元. 令非零元分别为X1,X2,··· ,Xk+n, 则

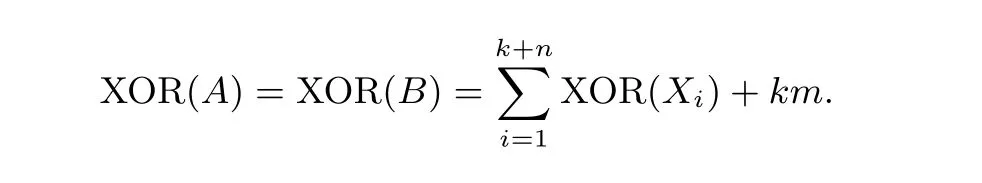
3 4 阶(3, 3) 迭代MDS 矩阵的构造

本节将使用无特殊结构的矩阵构造迭代MDS 矩阵, 并且使得矩阵迭代次数小于矩阵阶时就能满足MDS 性质. 在矩阵构造过程中, 为了获得更加轻量级的结果, 我们令矩阵由大量的零元和少数异或数小的元素组成. 本节给出了迭代次数为3 的4 阶迭代MDS 矩阵所含非零元个数的下界. 进一步地, 由于单位元是有限域非零元中异或数最低的元素, 在非零元个数达到下界时, 通过实验计算找到了迭代MDS 矩阵非零元中所含单位元个数的上界. 本节给出的搜索策略, 实现了对迭代次数为3, 非零元个数达到下界的4阶迭代MDS 矩阵的穷搜.

3.1 4 阶(k, 3) 迭代MDS 矩阵

本文主要研究4 阶迭代MDS 矩阵的构造. 在过去的构造方法中, 利用多项式的友矩阵构造MDS 矩阵, 至少需要迭代4 次才能得到一个MDS 矩阵. 因此, 我们先考虑迭代次数为3 的情况.

在构造之前, 首先要确定有限域F2m上4×4 矩阵M能够构造(k,3) 迭代MDS 矩阵时, 矩阵非零元θ(M)=k+4 的最小值. 在此之前, 先来看一个引理.

引理5 设A ∈Mn(F2m) 且θ(A)≤2, 则有θ(A2)≤2, 且θ(A2)=2 当且仅当A为如下三种情形:

(1)A中的两个非零元都在对角线上;

(2)A中的两个非零元关于对角线对称;

(3)A中的两个非零元在同一行或同一列且一个在对角线上.

证明: 当θ(A)≤2 时, 矩阵A可表示为A=a1E(i1j1)+a2E(i2j2), 其中a1,a2∈F2m且(i1,j1)/=(i2,j2). 因此有

从而

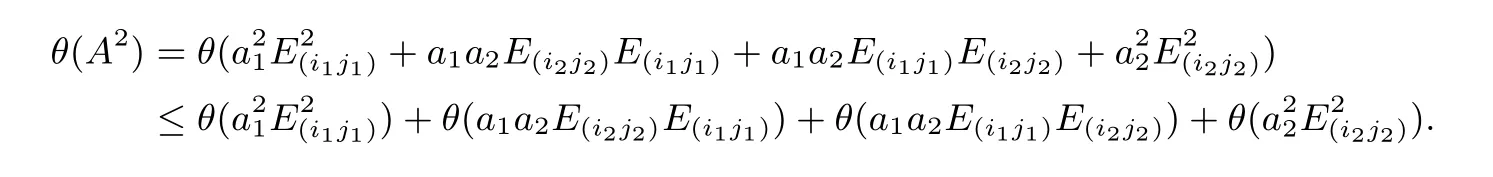
当θ(A)＜2,a1,a2至少有一个等于0, 则θ(A2)≤1.

当θ(A)=2,a1,a2/=0, 则有

定理1 设A ∈M4(F2m) 是(k,3) 迭代MDS 矩阵, 则k ≥3.

证明: 反证法. 假设A=PD+B是M4(F2m) 中2-XOR 矩阵, 其中P是置换矩阵,D是非奇异对角矩阵,θ(B)=2. 令P′=PD, 我们有

由引理5 可知θ(B2)≤2. 根据引理2, 对于任意矩阵M, 有θ(P′M) =θ(PDM) =θ(M). 因此,θ(P′3) =θ(P′) = 4 且θ(P′k1BP′k2) =θ(B) = 2(k1,k2是整数). 下面分四种情形证明θ(A3)＜16, 即A3不可能是MDS 矩阵.

情形1.θ(B2)≤1. 当θ(B2)≤1 时,θ(P′B2), θ(B2P′)≤1. 又θ(BP′B) =θ(BP′BP′) =θ((BP′)2)且θ(BP′) =θ(B) = 2, 因此θ(BP′B)≤2. 当θ(B2) = 0 时,θ(B3) = 0; 当θ(B2) = 1时,θ(B3) =θ(B2·B)≤2, 且θ(B3) = 2 时一定有B的非零元在同一行且都不在对角线上, 但此时θ(B2)=0, 矛盾. 从而θ(B3)≤1. 所以有

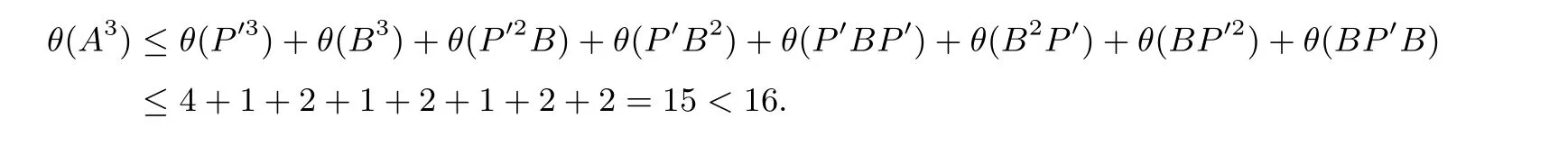
情形2.θ(B2) = 2 且B中的两个非零元都在对角线上. 此时,B为含两个非零元素的对角矩阵. 我们有

根据引理5 可知θ((BP′)2)≤2.

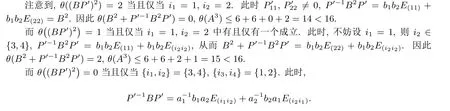
即矩阵P′-1BP′的非零元在第3 行第4 列和第4 行第3 列. 相同的方法计算可得矩阵P′-2BP′2的非零元在第1 行第2 列和第2 行第1 列, 与B的非零元位置相同. 因此θ(B+P′-2BP′2+P′-1BP′)≤4,θ(A3)≤6+4+4+0=14＜16.

情形4.θ(B2) = 2 且B中的两个非零元在同一行或同一列且一个在对角线上. 不妨设B中的两个非零元在同一行. 则对∀M ∈M4(F2m), θ(BM)≤4, 且BM的非零元都在同一行. 此时,

同理可证B中的两个非零元在同一列的情形.

综上所述, 对任意2-XOR 矩阵A, 都有θ(A3)＜16.

注4 在不考虑迭代次数的情况下,M4(F2m) 中迭代MDS 矩阵非零元个数至少为5, 且取到下界时,矩阵迭代次数至少为14[1].

定理1 给出的下界是建立在矩阵元素在有限域的基础之上, 实际上可以推广到有限域上的矩阵环中,得到一样的下界. 考虑矩阵环上的迭代次数为3 次的4 阶k-异或矩阵M=PD+B, 其中D为矩阵环上的对角矩阵(即有限域上的分块对角矩阵, 此时D有可能为奇异矩阵),P为矩阵环上的置换矩阵(即每行每列中只有一个位置是单位矩阵, 其余位置都为零矩阵). 当D为非奇异矩阵时, 即分块对角矩阵的每一个分块都是一个非奇异矩阵, 此时M中的非零元为矩阵环中的非奇异矩阵, 该类型矩阵M的非零元下界推导方法与定理1 证明方法类似(矩阵环中元素的非交换性使得个别细节地方证明略有不同); 当D为奇异矩阵时,M中的非零元可为矩阵环中任意的非零矩阵, 总可以找到矩阵M′=PD′+B′, 它和M具有相同的非零位置, 且每个非零位置上为非奇异矩阵, 并满足M迭代3 次后所含非零元的个数要小于等于M′迭代3 次后所含非零元的个数. 从而此种类型的M迭代3 次后能为MDS 矩阵(所含非零元个数必为16), 所含非零元的个数必大于等于M=PD+B,D为非奇异矩阵的情形.

根据定理1, 构造4×4 的(k,3) 迭代MDS 矩阵,k必须满足k ≥3. 而矩阵的非零元个数越少, 越有可能构造出实现代价更低的迭代MDS 矩阵. 本节接下来主要讨论k=3 时迭代MDS 矩阵的构造.

3.2 4 阶(3, 3) 迭代MDS 矩阵搜索

第一步, 非零元位置的选择. 确定7 个非零元的位置, 初步排除部分不满足迭代MDS 性质的3-XOR矩阵.

设M ∈M4(F2m) 为3-XOR 矩阵,M的非零元按其在矩阵中的行列位置, 从左到右从上到下分别设为X1,X2,··· ,X7, 则矩阵M3的元素是关于X1,X2,··· ,X7的多项式. 计算M3, 若M3的某个元素为零多项式, 则筛掉对应的M. 通过实验可以发现, 迭代3 次后矩阵元素都是关于X1,X2,··· ,X7的非零多项式的3-XOR 矩阵有120 个.

第二步, 矩阵的分类. 将120 个矩阵按置换相似进行分类, 并过滤掉部分迭代后MDS 条件多项式为零多项式的矩阵.

由引理4, 置换相似保持矩阵的迭代MDS 性质. 将矩阵按置换相似进行分类, 矩阵搜索空间减小为不同置换相似类的集合. 注意到, 置换相似变换仅改变矩阵非零元的位置不改变非零元数值. 在进行矩阵置换相似分类时, 可令X1,X2,··· ,X7= 1. 此时搜索空间变为120 个0, 1 矩阵的集合U, 对集合U做置换相似分类, 从而得到120 个矩阵的置换相似分类Ui={PMiP-1,P置换矩阵}, 1≤i ≤5, 见表2.

表2 矩阵置换相似分类Table 2 Permutation similarity classification

Ui中矩阵彼此间都是置换相似的, 它们有着相同的迭代MDS 性质和相等的异或数. 因此, 只用检查矩阵M1,M2,··· ,M5的迭代MDS 性质. 若M4(F2m) 中矩阵M是(3,3) 迭代MDS 矩阵, 则MDS条件多项式fM3必为非零多项式. 计算矩阵M1,M2,··· ,M5迭代3 次后对应矩阵的MDS 条件多项式fM3i(1≤i ≤5), 排除MDS 条件多项式fM3i为零多项式对应的矩阵Mi. 例如:

3.3 主要结果

尽可能多的取值为1. 令X1,X2,··· ,X7取值都为1 或任意6 个取值为1, 另1 个仍为未定元, 都使得fM31=fM32=0. 令X1,X2,··· ,X7中任意5 个取值为1, 另外2 个未定元分别设为X,Y(共有21 种取值可能), 此时存在部分取值使得fM31或fM32为关于X,Y的非零多项式. 从而(3,3) 迭代MDS 矩阵非零元取值1 的个数不大于5, 且非零元对1 的取值不是任意的, 结果见表3.

表3 含5 个1 的(3, 3) 迭代MDS 矩阵类型Table 3 Types of (3, 3) iterative MDS matrix containing five 1’s

我们重点关注M4(F24) 和M4(F28) 中的(3,3) 迭代MDS 矩阵, 分别找到了M4(F24) 和M4(F28)中异或数最小的(3,3) 迭代MDS 矩阵, 异或数分别为15 和30, 如矩阵

其中α和β分别为F24上生成多项式X4+X+1 和F28上生成多项式X8+X4+X3+X2+1 的根.则A3是MDS 矩阵且XOR(A)=XOR(α2)+XOR(α-1)+3×4=2+1+12=15;B3是MDS 矩阵且XOR(B)=XOR(β)+XOR(β-1)+3×8=3+3+24=30.

注意到, 当k ≥4 时,M4(F24) 中矩阵含有固定的异或数km ≥16, 不可能构造异或数比15 更小的(k,3) 迭代MDS 矩阵. 而对于(3,3) 迭代MDS 矩阵, 至少存在2 个非零元取值不为1, 因此矩阵异或数≥3×4+2×1 = 14, 且当且仅当矩阵5 个非零元取值为1 且另外两个非零元异或数均为1 时, 等号有可能成立. 我们对该类型矩阵实现了穷搜, 这类矩阵是不存在的, 即等号不能成立. 因此有命题1.

命题1M4(F24) 中(k,3) 迭代MDS 矩阵的异或数最小值为15, 且当且仅当k=3 时能取到最小值.

注5 在文献[5,8] 中, 作者利用4 阶友矩阵构造(3,t) 迭代MDS 矩阵, 在F24和F28上得到矩阵异或数最低分别为15 和33 的(3,4) 迭代MDS 矩阵. 在F24上, 我们构造的迭代MDS 矩阵, 在保证了矩阵非零元个数相同且矩阵异或数相等的情况下, 实现了迭代次数的降低. 而在F28上, 我们构造的迭代MDS 矩阵, 不仅迭代次数降低为3 次, 同时有着更低的异或数30.

此外, 我们也在有限域F25,F26,F27上对表3 中矩阵进行了搜索, 找到了异或数最低分别为18, 21,25 的(3,3) 迭代MDS 矩阵. 我们将本文得到的4 阶(3,3) 迭代MDS 矩阵结果与已知结果进行了比较,见表4.

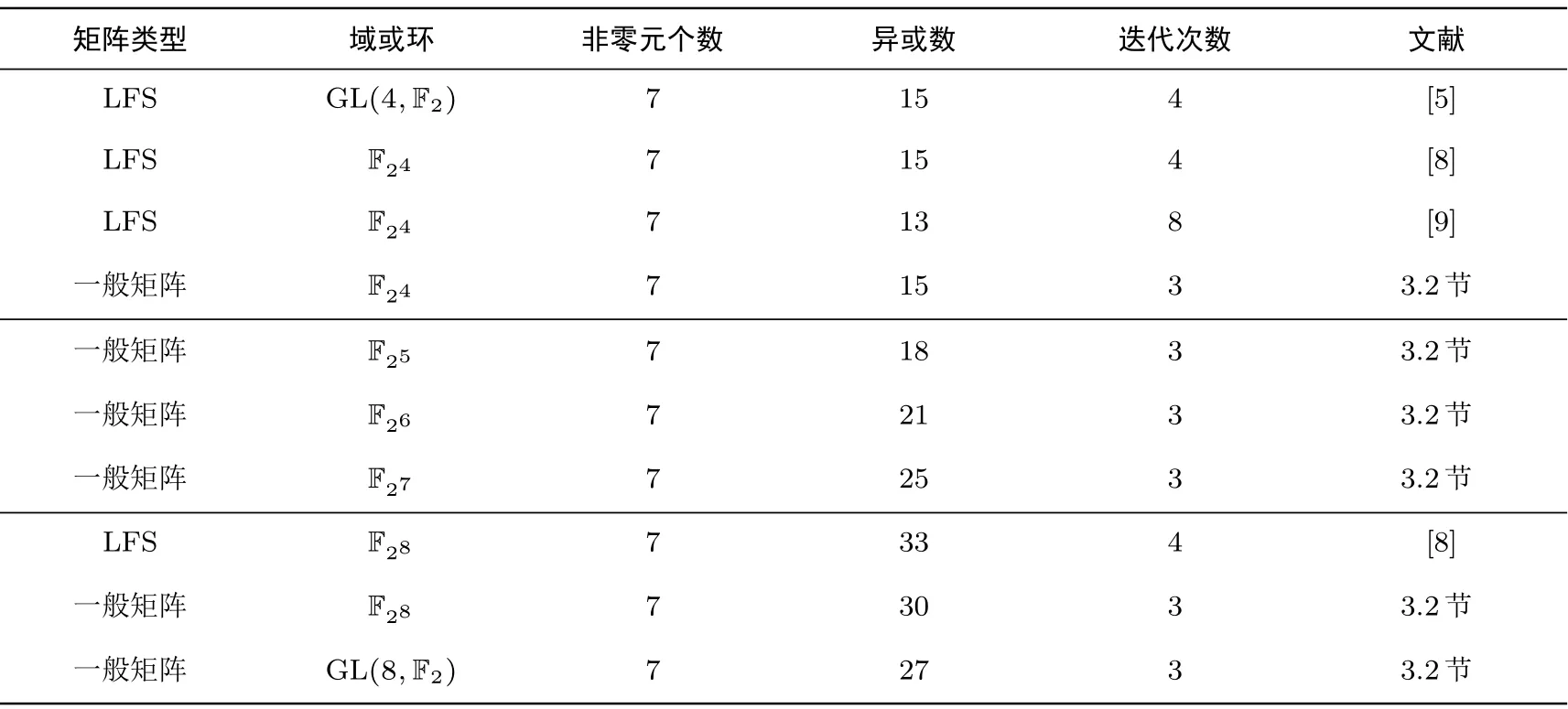
表4 4 阶(3, 3) 迭代MDS 矩阵结果的比较Table 4 Comparison of known results on (3, 3) iterative MDS matrices of order 4

4 其他类型迭代MDS 矩阵

4.1 4 阶(5, 2) 迭代MDS 矩阵

进一步减小4 阶迭代MDS 矩阵的迭代次数, 考虑M4(F2m) 中(k,2) 迭代MDS 矩阵的构造. 关于k的取值范围, 我们有以下定理.

定理2 设A ∈M4(F2m) 是(k,2) 迭代MDS 矩阵, 则k ≥5.

证明: 假设A=PD+B是M4(F2m) 中4-XOR 矩阵, 则

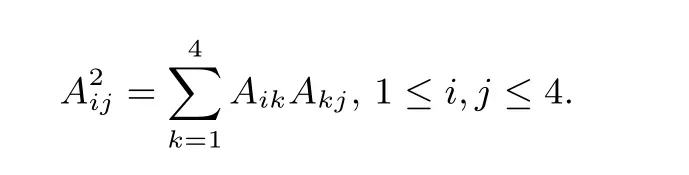
下面通过对矩阵B的秩Rank(B) 进行讨论, 分情况证明A2不可能是MDS 矩阵.

当Rank(B)＜4 时. 因为θ(B) = 4, 矩阵B至少存在某一行或某一列全是零元, 从而矩阵A存在某一行或某一列只含一个非零元. 不妨设A的第一行只有一个非零元且A1i/=0. 则要使得A2第i行不含零元, 必有Ai1,Ai2,Ai3,Ai4/= 0. 又因为θ(A) = 8, 则另外两行有三个非零元, 从而矩阵A必还存在另一行也只含一个非零元, 设该非零元是Ai′j, 则i′/=1, j/=i(否则A不是k-XOR 矩阵). 同样地, 要使得A2第j行不含零元, 则必有Aj1,Aj2,Aj3,Aj4/= 0, 这与θ(A) = 8 矛盾. 即Aj1,Aj2,Aj3,Aj4中至少有一个为0, 因此一定有θ(A2)＜16. 当矩阵A的某一列只有一个非零元, 类似可证.

当Rank(B) = 4 时. 因为θ(B) = 4, 矩阵B每行每列只含一个非零元, 即矩阵A每行每列含有两个非零元. 要使得A2是MDS 矩阵, 则θ(A2) =θ(P′2+P′B+BP′+B2) = 16, 其中P′=PD.又因为θ(P′2) =θ(P′B) =θ(BP′) =θ(B2) = 4, 所以矩阵P′2, P′B, BP′, B2的非零元所在位置互不相同, 每个非零元刚好是矩阵A2对应位置的元素. 且由于矩阵P, B每行每列均只含一个非零元, 所以P′2, P′B, BP′, B2的非零项都只是A中某两个元素的乘积, 此时A2的每一个元素都仅是A中某两个元素的乘积, 即(A2)ij=AikAkj,1≤i,j,k ≤4.

假设矩阵A第i行的两个非零元分别为Aij1,Aij2, 第i列的两个非零元分别为Ak1i,Ak2i. 则矩阵A2存在二阶子方阵

因此A2不可能是MDS 矩阵.

采用第3 节同样的搜索策略, 在F24和F28上, 我们找到了异或数最小的(5,2) 迭代MDS 矩阵, 异或数分别为23 和49, 如矩阵

其中α和β分别为F24上生成多项式X4+X+1 和F28上生成多项式X8+X4+X3+X2+1 的根.则A2是MDS 矩阵且XOR(A)=XOR(α)+2XOR(α-1)+5×4=1+2+20=23;B2是MDS 矩阵且XOR(B)=3XOR(β)+5×8=3×3+40=49.

命题2M4(F24) 中(k,2) 迭代MDS 矩阵的异或数最小值等于23, 此时矩阵非零元素个数为9, 迭代次数等于2.

在有限域F25,F26,F27上的搜索结果, 见表5.

表5 4 阶(5, 2) 迭代MDS 矩阵结果Table 5 Results of (5, 2) iterative MDS matrices of order 4

4.2 4 阶(2, 4) 迭代MDS 矩阵

基于迭代MDS 矩阵通过循环矩阵来实现最优扩散的特性, 使得优化迭代MDS 矩阵存在两个方向:

(1) 减小矩阵的迭代次数, 从而缩短实现过程中的时间延迟; (2) 减少矩阵的非零元个数, 从而降低矩阵的异或数. 第3 节及4.1 节正是通过减小矩阵的迭代次数获得更优的迭代MDS 矩阵. 本节主要是通过减小矩阵的非零元个数, 来构造M4(F2m) 中迭代次数等于矩阵阶数但非零元个数小于7 的迭代MDS 矩阵.

定理3 设A ∈M4(F2m) 是(k,4) 迭代MDS 矩阵, 则k ≥2.

证明: 假设A=PD+B是M4(F2m) 中1-XOR 矩阵, 即矩阵B只含一个非零元. 令P′=PD,则

根据定理2 可知,若A2∈M4(F2m)是迭代次数等于2 的迭代MDS 矩阵,则θ(A2)≥9. 因此,A4=(A2)2不可能是MDS 矩阵, 即A不可能是(k,4) 迭代MDS 矩阵.

因此, 矩阵迭代次数与阶数相同都等于4 时, 矩阵非零元个数的最小值为6. 根据定理1 和2 可知, 要使得4 阶2-XOR 矩阵是迭代MDS 矩阵, 则其迭代次数必≥4. 接下来考虑(2,4) 迭代MDS 矩阵的构造. 根据第3 节的搜索策略, 通过对2-XOR 矩阵的筛选, 满足迭代4 次后的矩阵不含零元, 且MDS 条件多项式不等于零的矩阵仅有两类不同的置换相似类. 用未知元X1,X2,··· ,X6分别表示非零元, 筛选和分类结果见表6.

表6 (2, 4) 迭代MDS 矩阵类型Table 6 Permutation similarity classes of (2, 4) iterative MDS matrices

显然, 矩阵M1即为文献[2] 中所提出的稀疏型DSI 矩阵. 进一步搜索, 在F24上可得异或数最小为10 的(2,4) 迭代MDS 矩阵

其中α是生成多项式X4+X+1 的根. 这正是文献[2] 中所构造的最优稀疏DSI 矩阵. 除此之外, 置换相似类W2也可以构造同样优异的迭代MDS 矩阵. 取

当A ∈M4(F24),α是生成多项式X4+X+1 的根时,A4是MDS 矩阵且XOR(A) = 2XOR(α)+2×4 = 10; 当A ∈M4(F28),α是生成多项式X8+X4+X3+X2+1 的根时,A4也是MDS 矩阵且XOR(A)=2XOR(α)+2×8=22.

注6 异或数为10, 是M4(F24) 中非零元个数为6, 迭代次数为4 的迭代MDS 矩阵的异或数所能达到的最小值(文献[1], 引理18). 异或数为22 也是M4(F28) 中非零元个数为6, 迭代次数为4 的迭代MDS 矩阵的异或数所能达到的最小值. 这是由于k ≥3 时,M4(F28) 中矩阵含有固定的异或数km ≥24,不可能构造异或数比22 更小的(k,4) 迭代MDS 矩阵. 而对于(2,4) 迭代MDS 矩阵, 至少存在2 个非零元取值不为1, 且在生成多项式为X8+X4+X3+X2+1 的域F28中, 非0, 1 的元素的异或数最小等于3.

我们将得到的4 阶(2,4) 迭代MDS 矩阵结果与已知结果进行了比较, 见表7.

表7 4 阶(2, 4) 迭代MDS 矩阵结果的比较Table 7 Comparison of known results on (2, 4) iterative MDS matrices of order 4

4.3 5 阶(4, 4) 迭代MDS 矩阵

对于5 阶矩阵, 经过实验计算我们发现, 要使得矩阵迭代次数小于矩阵阶数, 如取迭代次数为4 时, 必有矩阵非零元个数≥9. 考虑构造(4,4) 迭代MDS 矩阵. 我们找到了域F28上最小异或数为38 的(4,4)迭代MDS 矩阵. 如矩阵

其中α是F28上生成多项式X8+X4+X3+X2+1 的根.A4是MDS 矩阵且XOR(A)=XOR(α)+XOR(α-1)+4×8=3+3+32=38.

类似的, 文献[5,6,8] 利用友矩阵构造5 阶迭代MDS 矩阵时, 矩阵非零元个数等于9, 即构造的是(4,5) 迭代MDS 矩阵. 根据迭代矩阵的第二个优化方向, 本文对迭代次数等于5 的5 阶矩阵, 将其非零元个数减小为8 个, 对(3,5) 迭代MDS 矩阵进行了搜索. 在F28上, 我们找到了异或数最小等于35 的(3,5) 迭代MDS 矩阵. 如矩阵

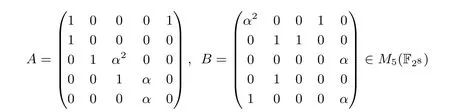
其中α是生成多项式X8+X7+X6+X+1 的根.A5和B5都是MDS 矩阵且XOR(A)=XOR(B)=2XOR(α)+XOR(α2)+3×8=2×3+5+24=35. 这个结果也是该域上异或数最低的迭代MDS 矩阵,通过本文的搜索策略可以找到所有异或数最低的(3,5) 迭代MDS 矩阵, 包括稀疏DSI(3,5) 迭代MDS矩阵[2], 另外还找到了迭代次数等于5, 异或数为35 的一般类型(3,5) 迭代MDS 矩阵, 结果比较见表8.

表8 5 阶迭代MDS 矩阵结果的比较Table 8 Comparison of known results on iterative MDS matrices of order 5

注7 矩阵A即为文献[2] 中构造的5 阶稀疏DSI 迭代MDS 矩阵, 此处计算该DSI 矩阵的异或数使用的是本文统一的度量方式, 在文献[2] 中通过优化矩阵实现过程, 使实现该矩阵只需31 个异或数.

5 总结

本文首先研究了迭代次数为3 的4 阶迭代MDS 矩阵所含非零元个数的下界, 证明了其下界为7.通过非零元位置的选择、矩阵的置换相似分类和非零位置元素的确定, 实现了非零元个数达到下界7 的4 阶迭代MDS 矩阵的穷搜. 进一步为了得到更加轻量的结果, 考虑7 个非零元中可以取值为1 的个数.实验结果表明, 7 个非零元中最多5 个可以取值为1. 在此情形下, 我们在F24上找到了非零元个数达到最小值7, 异或数也达到最小值为15 的4 阶迭代MDS 矩阵, 在保证矩阵非零元个数相同且异或数相等的情况下, 实现了迭代次数的降低; 在F28上找到了非零元个数达到最小值7, 异或数为30 的4 阶迭代MDS 矩阵, 实现了迭代次数的降低同时也有着更低的异或数. 随后, 我们也证明得到了迭代次数分别为2、4 的4 阶迭代MDS 矩阵, 以及通过实验得到迭代次数为4 的5 阶迭代MDS 矩阵所含非零元个数的下界. 利用同样的搜索策略, 我们也找到了非零元个数达到下界, 矩阵异或数也达到最小值的一般型轻量迭代MDS 矩阵.