逻辑推理初步章节小测

陈选明

(江西师范大学附属中学)

(本试卷共13小题,满分150分,考试用时120分钟)

一、单选题(本题共6小题,每小题9分,共54分.在每小题给出的选项中,只有一项是符合题目要求的.)

1.用反证法证明命题:“已知a,b是自然数,若a＋b≥4,则a,b中至少有一个不小于2”,提出的假设应该是( ).

A.a,b中两个都不小于2 B.a,b中至少有一个小于2

C.a,b都小于2 D.a,b中至多有一个小于2

2.“正弦函数是奇函数,g(x)＝sin(x＋x2)是正弦函数,因此g(x)＝sin(x＋x2)是奇函数”,以上推理( ).

A.结论正确 B.小前提不正确 C.大前提不正确 D.全部正确

A.1项 B.k项 C.2k－1项 D.2k项

4.图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,图7中,小正方体木块的总数是( ).

A.66 B.91 C.107 D.120

5.某学校为贯彻落实教育部新时代体育教育精神,面向全体学生开设了体育校本课程.学生小瑜选完课程后,根据小瑜的兴趣爱好对他选择的课程进行猜测.甲说:“小瑜选的不是足球,选的是篮球.”乙说:“小瑜选的不是篮球,选的是羽毛球.”丙说:“小瑜选的不是篮球,也不是乒乓球.”已知三人中有一人说的全对,有一人说的对了一半,剩下的一人说的全不对,由此推断小瑜选择的课程( ).

A.可能是乒乓球 B.可能是足球 C.可能是羽毛球 D.一定是篮球

6.杨辉是我国南宋末年的一位杰出的数学家,其著作《详解九章算术》中画了一张表示二项式展开式后的系数构成的三角形数阵(如右图),称做“开方做法本源”,现简称为“杨辉三角”,比西方的＂帕斯卡三角形”早了300多年.若用A(m,n)表示三角形数阵中的第m行第n个数,则按照自上而下,从左到右顺次逐个将杨辉三角中二项式系数相加,加到A(100,3)这个数所得结果为( ).

A.298＋4851 B.299＋4950

C.2100＋5000 D.2101＋5050

二、多选题(本题共2小题,每小题9分,共18分.在每小题给出的选项中,有多项是符合题目要求的.全部选对的得9分,有选错的得0分,部分选对的得4分.)

7.任取一个正整数,若是奇数,就将该数乘3加1;若是偶数,就将该数除以2.反复进行上述运算,经过有限次步骤,必进入循环圈1→4→2→1.这就是数学史上著名的“冰雹猜想”(又称“角谷猜想”).如果对于正整数m,经过n步变换,第一次到达1,就称为n步“雹程”.如取m＝3,由上述运算法则得出3→10→5→16→8→4→2→1,共需经过7个步骤变成1,得n＝7.则下列命题正确的有( ).

A.若n＝2,则m只能是4 B.当m＝17时,n＝12

C.随着m的增大,n也增大 D.若n＝7,则m的取值集合为{3,20,21,128}

8.设正整数n＝a0·30＋a1·31＋…＋ak－1·3k－1＋ak·3k,其中对于任意的0≤i≤k,ai∈{0,1,2}.函数f:N*→N满足f(n)＝a0＋a1＋…＋ak,则( ).

A.f(3n)＝f(n) B.f(3n＋4)＝f(9n＋10)

C.f(3n＋5)＝f(n)＋2 D.f(9n＋5)＝4

三、填空题(本题共2小题,每小题9分,共18分.)

9.若等差数列{an}的前n项和为Sn,则S2n－1＝(2n－1)an.由类比推理可得:在等比数列{bn}中,若其前n项的积为Pn,则P2n－1＝________.

10.在平面内,余弦定理给出了三角形的三条边与其中的一个角之间的关系.应用余弦定理,可以从已知的两边和夹角出发,计算三角形的第三边.我们把四面体与三角形作类比,并使四面体的面对应三角形的边,四面体各面的面积对应三角形各边的边长.而三角形两边的夹角,对应四面体两个面所成的二面角,这样可以得到“四面体的余弦定理”.现已知一个四面体V-ABC,S△VBC＝S△VAC＝,S△VAB＝2,二面角C-VA-B＝45°,二面角B-VC-A＝60°,二面角A-VB-C为直二面角,则△ABC的面积为_________.

四、解答题(本题共3小题,每小题20分,共60分.解答时应写出文字说明、证明过程或演算步骤.)

11.我们知道,判断直线与圆的位置关系可以用圆心到直线的距离进行判断,那么直线与椭圆的位置关系有类似的判别方法吗? 请同学们进行研究并完成下面问题.

(1)设F1,F2是椭圆＝1(a＞b＞0)的两个焦点,点F1,F2到直线l:mx＋ny＋p＝0(m,n不同时为0)的距离分别为d1,d2,且直线l与椭圆M相切,试求d1d2的值;

(2)试写出一个能判断直线与椭圆的位置关系的充要条件,并给出证明.

12.《见微知著》谈到:从一个简单的经典问题出发,从特殊到一般,由简单到复杂.从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,是发现新问题、新结论的重要方法.

阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法,常用的途径有整体观察、整体设元、整体代入、整体求和等.

波利亚在《怎样解题》中指出:“当你找到第一个蘑菇作出第一个发现后,再四处看看,他们总是成群生长.”类似问题,我们有更多的式子满足以上特征.

例如,在x＞0的条件下,当x为何值时,x＋有最小值,最小值是多少?1时,x＋有最小值,最小值为2.

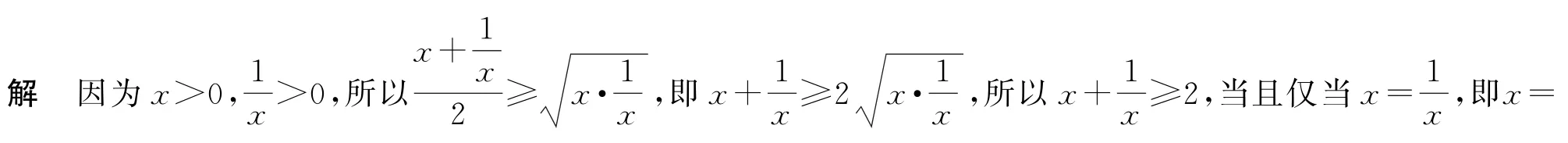
请根据阅读材料解答下列问题.

(1)已知ab＝1,求下列各式的值:

13.问题:正数a,b满足a＋b＝1,求的最小值.

学习上述解法并解决下列问题.

(1)若正实数x,y满足xy＝3x＋y,求x＋y的最小值;

(2)若实数a,b,x,y满足＝1,试比较a2－b2和(x－y)2的大小,并指出等号成立的条件;

(3)利用(2)的结论,求代数式M＝的最小值,并求出使得M最小的m的值.