四面体垂心研究的进展*
曾建国
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
与三角形中三条高交于一点(垂心)的情形不同,四面体的四条高不一定交于一点.因此,当人们运用类比的思维方法尝试将垂心概念引申到四面体时遇到了不少困难.尽管如此,人们仍然在四面体垂心研究的道路上不懈努力、不断探索,取得了丰硕的研究成果.本文对四面体垂心研究的历程进行回顾,并介绍近年来有关四面体垂心研究的进展.
1 传统意义的四面体垂心
按传统意义的三角形垂心定义(三条高的交点)类比至四面体中时,我们发现,只有一类特殊的四面体——垂心四面体(三组对棱互相垂直的四面体)的四条高交于一点,此类四面体具有传统意义的垂心.
在四面体中,如果两组对棱分别垂直,则第三组对棱也垂直,即有
命题1[1]四面体的四条高交于一点的充要条件是两组对棱分别垂直.
定义1垂心四面体的四条高交于一点,称为四面体的垂心.
在三角形中,垂心、重心、外心三点共线,即有欧拉线定理(Euler,1765年).
命题2[2]三角形的外心O、重心G、垂心H共线,且OG∶GH=1∶2.
命题2引申至垂心四面体中,就得垂心四面体的欧拉线定理.
命题3[3]垂心四面体的外心O、重心G、垂心H共线,且OG∶GH=1∶1.
1995年,冯华根据命题3及四面体的莱布尼兹公式[4]证明了垂心四面体的垂心的一个性质.
命题4[5]设垂心四面体A1A2A3A4的垂心为H,外接球半径为R,则
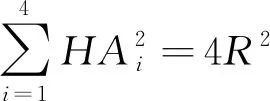
(1)
三角形中与垂心有关的其他性质也可以类比移植到垂心四面体中.例如,人们将三角形九点圆定理推广至垂心四面体中,得到了垂心四面体的两类“十二点球定理”.
第1类十二点球定理是法国数学家普鲁海(Prouhet)于1863年发现的.
命题5[2,6]垂心四面体中,垂心到四面体各顶点的连线的第一个3等分点、四面体各面的垂心和重心,共12点共球,其球心为外心与垂心连线的第二个3等分点,半径为四面体外接球半径的三分之一.
第2类十二点球定理是法国数学家坦佩莱(Temperley)与莱维(Lévy)于1881年发现的.
命题6[2,7]垂心四面体中,每个侧面三角形的三条高的垂足、6条棱的中点共12点共球,球心是四面体的重心.
但由于传统意义的垂心概念仅适用于垂心四面体,因此所有推广的结论也仅对垂心四面体成立,不适用于一般四面体.
2 垂心概念在四面体中的其他类比推广
由于传统意义的垂心概念无法类比推广至一般的四面体中,致使三角形垂心的大量优美性质难于类比推广至四面体中.于是人们另辟蹊径,尝试用其他方法推广垂心概念.
2.1 蒙日点
2010年,耿恒考[8]类比三角形的高线并引申得到四面体的“高面”——过四面体的一条棱的中点垂直于对棱的平面,并证明了四面体的6个高面必交于一点,称其为四面体的“垂心”.事实上,这样类比得到的“垂心”就是四面体的“蒙日点”,是法国数学家蒙日(G.Monge)于1811年发现的[2].
命题7四面体的每条棱的中点向它的对棱引垂面,6个垂面必交于一点M.
另一位法国数学家曼海姆(V.M.A.Manheim,1831-1906)也作过一种类比推广,用另一种方法得到一般四面体的“垂心”(也与蒙日点合同)[2].
命题8设四面体A1A2A3A4顶点Ai所对侧面三角形的垂心为Hi,四面体(自顶点Ai引出)的高线为hi,则由hi与Hi(i=1,2,3,4)确定的四个平面交于一点H.
事实上,命题8中的垂心H与蒙日点M合同(曼海姆本人已证明)[1].因此我们将命题7与命题8中定义的四面体的“垂心”统称为四面体的蒙日点.
有趣的是,四面体的外心、重心、蒙日点三点也共线,即有[2]
命题9四面体的外心O、重心G、蒙日点M三点共线,且OG∶GM=1∶1.
对照命题2可知,在垂心四面体中,蒙日点与垂心为同一点.因此,一般四面体的蒙日点是四面体垂心概念的推广.因此我们完全有理由把命题9中的直线称为一般四面体的“欧拉线”.
2.2 伪垂心
一般四面体的伪垂心概念是熊曾润教授在2005年建立的.
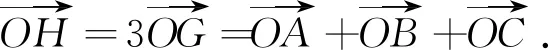
从这一向量表示形式的角度进行类比,可得四面体的伪垂心概念如下[9]
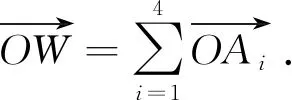
伪垂心也在四面体的欧拉线上,即有[9]
命题10四面体的外心O、重心G、伪垂心W三点共线,且OG∶GW=1∶3.
伪垂心是四面体一个新的特殊点.根据定义2可以推得伪垂心的许多有趣性质,例如[9]
命题11设四面体A1A2A3A4的外接球球心为O、半径为R,伪垂心为W,则
2.3 欧拉球心
2005年,熊曾润教授将三角形的九点圆(又称欧拉圆)引申推广至四面体中,得四面体的欧拉球面概念[10-11].
定义3设四面体A1A2A3A4的外接球球心为O、半径为R,顶点Aj所对的侧面记作Δj(j=1,2,3,4),
我们先讨论四面体的欧拉球心与垂心的关系.
命题12四面体的外心O、重心G、欧拉球心E三点共线,且OG∶GE=1∶1.
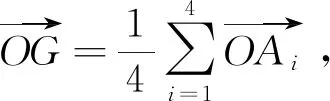
对照命题12与命题9即知四面体的欧拉球心与蒙日点合同.进而可知,垂心四面体的欧拉球心就是其垂心[12].
对于任一给定的四面体,耿恒考定义的垂心[8]、蒙日点[2]、曼海姆定义的垂心[2]、欧拉球心[10-11]均为同一点(以下统一称欧拉球心).类比推广的角度、方法各不相同,得到的竟是同一个点!真可谓“殊途同归”.这一定算得上是几何研究历史上的一件趣事.
综上所述可知:任一给定四面体存在惟一的欧拉球心;垂心四面体的欧拉球心就是其垂心.由此可见,四面体的欧拉球心是垂心四面体的垂心概念的推广.垂心四面体的垂心具有一般四面体欧拉球心的所有性质,而一般四面体的欧拉球心不一定具有垂心四面体垂心的某些性质.
因此,研究四面体欧拉球心的性质比研究垂心性质具有更为广泛的意义.
现列举四面体欧拉球心的两个性质.
命题13[12]四面体的欧拉球心到一棱中点的距离等于外心到对棱中点的距离.即:若四面体A1A2A3A4的外心为O、欧拉球心为E,M、N分别是棱A1A2、A3A4的中点,则有OM∥NE且OM=NE.
前文所述垂心四面体垂心的一个性质(命题4)也可以推广至一般四面体中.

与欧拉球心有关的四面体欧拉球面的性质更为精彩.
四面体欧拉球面是三角形九点圆在四面体中的类比推广,由此得到的一系列共球点性质令人叹为观止,如
命题15[9,13]四面体A1A2A3A4的欧拉球面必通过12个特殊点,即:各顶点Aj与伪垂心H连线的中点Mj(j=1,2,3,4);各侧面Δj的欧拉球心Ej(j=1,2,3,4);过点Ej作直线与直线AjH垂直相交的垂足Dj(j=1,2,3,4).
命题16[11,14]设四面体A1A2A3A4的外接球球心为O、半径为R,其伪垂心为H,顶点Aj所对的侧面Δj的欧拉球心为Ej,过点Ej作直线与直线AjH垂直相交于Dj,且设此直线交外接球面O于Bj、Cj两点,则ΔAjBjCj的九点圆必在四面体A1A2A3A4的欧拉球面上(j=1,2,3,4).
命题16表明:四面体的欧拉球面通过4×9=36个特殊点.
回顾四面体垂心研究的历程和研究成果发现,熊曾润先生所作的工作是最重要的.
3 四面体垂心概念的后续研究
四面体垂心概念的研究历程展现了类比推理的巧妙方法和强大威力,同时也启发我们可进一步开展本课题研究的方向.事实上,以下两方面的研究已经取得了初步进展:将四面体的垂心、欧拉球心、重心等概念一般化,进而研究四面体的k号心[13,15];将四面体的垂心(包括其他心)概念进一步推广至球内接多面体[9]、n维单形[16]、乃至n维有限点集[17-18]中.
(谨以此文纪念熊曾润教授逝世6周年)
——三角形一个共线点命题的空间移植

