基于SE(3)群局部标架的5/6 Dofs CB 壳单元1)
张腾 刘 铖 †,, 张志娟 刘绍奎
* (北京理工大学宇航学院,北京 100081)
† (中物院高性能数值模拟软件中心,北京 100088)** (北京应用物理与计算数学研究所,北京 100088)
†† (北京空间飞行器总体设计部,北京 100094)
引言
多柔体系统的动力学过程通常包含柔性部件的大范围刚体运动与弹性变形.柔性部件作大范围刚体运动时引起的转动与弹性变形引起的转动是导致多柔体系统动力学过程呈现较高非线性的主要原因.如何有效降低多柔体系统动力学过程的非线性程度,特别是几何非线性,是多柔体系统动力学领域面临的挑战之一.
近来,李群局部标架(local frame of Lie group,LFLG)[1]思想与几何精确方法(geometrically exact formulation,GEF)[2]的进一步融合,有效规避了刚体转动导致的几何非线性.如Sonneville 等[3]、刘铖和胡海岩[1]基于SE(3) 群(the special Euclidean group)局部标架开发了几何精确梁单元,数值结果表明任意刚体运动下单元广义弹性力、广义惯性力及他们的雅可比矩阵保持不变,从而消除了刚体运动带来的几何非线性.而且,在处理几何非线性问题时,牛顿迭代过程中系统的雅可比矩阵不需要更新或者较少更新,这使动力学过程的计算效率得到明显改善.最近,Zhang 等[4]基于SE(3)群局部标架开发了含drilling 自由度的几何精确板/壳单元,数值结果表明该单元继承了李群局部标架下几何精确梁单元中的优良特性,如几何非线性程度降低、计算效率显著改善等.事实上,李群局部标架思想几乎可以和所有考虑几何非线性的梁、板/壳以及实体单元相结合,使其在计算中规避刚体运动导致的几何非线性,如李群局部标架下基于绝对节点坐标方法(absolute nodal coordinate formulation,ANCF)[5]的三维全参数梁单元、李群局部标架下基于绝对节点坐标方法的三维全参数板/壳单元等,详细内容可参见作者之前的工作[1,6].
基于SE(3)群局部标架的几何精确单元虽拥有上述良好特性,但单元的实现过程相对困难,尤其是广义弹性力及其雅可比矩阵的计算.其难点可以归纳为两个方面,一是如何保证空间离散过程中插值算法的客观性.Crisfiled 与Jelenić[7]曾指出对转动伪矢量直接进行有限元插值将违背应变的客观性与材料路径的无关性.为此,文献[1,3]均在SE(3)群上空间离散时采用了相对插值,保证了离散应变的客观性.然而,采用相对插值进一步导致广义弹性力的计算及线性化过程变得复杂.如Sonneville[8]在其博士论文中通过Newton-Raphson 迭代获取单元内部相对插值的参考点,导致弹性力及其线性化过程更加复杂.Zhang 等[4]通过数值算例验证了选取不同节点作为参考点对收敛结果的影响可忽略不计.因此,通常选取单元第一个节点作为相对插值的参考点,但这仍没有规避相对插值带来的复杂性.二是如何处理有限元离散与变分操作的先后顺序.众所周知,线性空间中不区分先离散再线性化(称为离散一致线性化)与先线性化再离散(称为连续一致线性化),但在SE(3)群中不然.张腾等曾按照这两种方式严格推导了对应版本的SE(3)群局部标架下几何精确板/壳单元,发现连续一致线性化版本的几何精确板/壳单元在动力学仿真过程中遭遇收敛性问题.先离散再线性化版本的板/壳单元不存在收敛性问题,但该版本广义弹性力的计算及线性化过程比较复杂.
基于连续体(continuum-based) 的壳[9](简称CB 壳)理论有望为规避上述满足客观性的插值及离散与变分操作顺序带来的复杂性提供新的解决思路.CB 壳单元的有限变形是建立在三维实体单元上,其广义弹性力及雅可比矩阵是通过实体单元的广义弹性力及雅可比矩阵以及实体单元上下表面与参考中面之间的节点转换矩阵得到.显然,实体单元的广义弹性力及雅可比矩阵在计算时只包含平动自由度,无转动自由度.平动属于线性空间,在线性化过程中不存在有限元离散与变分操作先后顺序的问题.而且,在线性空间中插值算法的客观性可自然满足,无需使用相对插值即可保证离散应变的客观性.因此,李群局部标架思想与CB 壳理论的结合可以规避SE(3)群局部标架下几何精确板/壳单元中由插值和离散与变分操作所导致单元实现过程过于复杂的问题.
经典CB 壳单元最初由Ahmad 等[10]于1970 年提出.Parisch[11]、Hughes和Liu[12-13]先后将CB 壳模型推广至可用于非线性分析的格式.不同的是,Parisch 使用节点局部坐标系与全局坐标系之间的旋转角描述截面转动,Hughes和Liu 则使用沿厚度方向的矢量变化描述截面转动.目前,CB 壳模型已经应用于多个领域.如庄茁和成斌斌[14]发展了基于CB 壳单元的扩展有限元,用于模拟三维任意扩展裂纹问题.Bergman和Yang[15]基于完全的拉格朗日方法采用CB 壳单元对形状记忆聚合物建立有限元模型,成功应用于航空航天领域.Momenan[16]将CB 壳单元用于软生物组织的动力学分析.Han 等[17]采用CB 壳单元模拟流固耦合问题中经历大变形的柔性薄壳结构.
有限元方法中低阶梁、板/壳和实体单元普遍存在薄膜(面内)、剪切和厚度闭锁[18]问题,CB 壳单元也不例外.针对本文所提出基于SE(3)群局部标架的CB 壳单元,分别采用Hellinger-Reissner 两场变分原理[19-20]和假设自然应变(assumed natural strain,ANS)方法[21]缓解面内闭锁和横向剪切闭锁.
为包含drilling 自由度,本文借鉴Fox和Simo[22]在几何精确壳中引入运动约束的方法,并将该方法应用于5 Dofs CB 壳单元,提出了含有drilling 自由度的CB 壳单元-6 Dofs CB 壳单元.本文引入drilling 自由度的目的有两个,一是保证CB 壳单元可直接处理含约束的多体系统(如壳与梁、壳与壳连接等结构);二是6 Dofs CB 壳单元可完全消除刚体运动带来的几何非线性.Zhang 等[4]在最近的工作中通过数值算例验证了基于SE(3)群局部标架5 Dofs 几何精确壳单元只能部分消除刚体运动带来的几何非线性,而6 Dofs 几何精确壳单元可完全消除几何非线性.类似地,本文所提出的6 Dofs CB 壳也可以完全消除刚体运动带来的几何非线性.
为解决上述SE(3)群局部标架下几何精确壳单元存在的两个问题,本文融合李群局部标架思想与经典CB 壳理论推导基于SE(3) 群局部标架的5 DoFs CB 壳单元.该单元可有效规避几何精确壳单元中插值带来的复杂性,单元离散应变张量的客观性可自然得到满足.同时,该单元在线性化过程中不存在有限元离散与变分操作先后顺序的问题,这进一步简化了单元广义弹性力及其雅可比矩阵的计算.为提高单元收敛性,本文分别采用Hellinger-Reissner 两场变分原理和ANS 方法缓解面内和剪切闭锁.为完全消除刚体运动导致的几何非线性以及方便处理组合体结构,在5 Dofs CB 壳单元基础上引入drilling 自由度,提出了6 Dofs CB 壳单元.最后,通过5 个静力学算例验证了所提出CB 壳单元的收敛精度,一个多体系统动力学算例验证了CB 壳单元在计算过程中消除刚体运动带来的几何非线性,从而使系统的广义弹性力、广义惯性力及其雅可比矩阵满足刚体运动的不变性.
1 基于SE(3)群局部标架的CB 壳单元运动描述及本构关系
1.1 运动描述
在经典的CB 壳理论中,通常采用如下的假设:(1)纤维保持直线(修正的Mindlin-Reissner 假设);(2)平面应力条件;(3)动量源于纤维的伸长,并且沿纤维方向忽略动量平衡[9].在上述假设基础上,本文还假定板/壳单元厚度不变.
图1 所示为8 节点CB 壳单元,白色和黑色节点分别表示从属节点(slave nodes)和主控节点(master nodes).每个从属节点有3 个平动自由度,每个主控节点有5 个独立的自由度,包括3 个平动和2 个转动.ξ=[ξ η ζ]T为母单元坐标(自然坐标),ζ对应的每一个面称为层,通常将ζ=0 看作单元参考中面.沿着ζ轴的线称为纤维,沿着纤维方向的单位矢量称为方向矢量.e1,e2和e3为惯性坐标系下的单位正交基矢量.

图1 8节点CB 壳单元Fig.1 Configuration of an eight-node CB shell element
从属节点和主控节点之间的关系可表示为

式中,h0为壳单元厚度,xI+和xI-∈ R3为单元顶面和底面上从属节点的位置矢量,xI∈ R3表示参考中面上节点的位置,I +和I-分别对应壳单元上表面和下表面从属节点编号,I为主控节点编号,其中,I +=1,2,···,4,I-=5,6,···,8,I=1,2,···,4.pI∈S2为主控节点I沿纤维方向的单位矢量,满足pI=RIe3,S2为R3空间中的单位球[23],RI为当前构形中主控节点I的方向矢量相对于e3的旋转.以主控节点I为原点,通过RI可建立节点I局部随体坐标系与惯性坐标系之间的关系,本文称此局部随体坐标系为局部标架[1].事实上,壳单元中面上任意一点处均存在局部标架.在当前构形中,CB 壳单元上任意一点的位置矢量可表示为

式中,φ为当前构形中单元的广义坐标,为标准等参三维线性形函数[24],I3为3 × 3 单位矩阵,NI*的表达式如下

将式(1) 作简单变分操作可建立局部标架下CB 壳单元从属节点平动自由度与主控节点的平动和转动自由度之间的变换关系,如下


SE(3)群局部标架下CB 壳单元的插值本质上是在线性空间中对实体单元的从属节点进行插值,获得实体单元的广义弹性力及其雅可比矩阵,之后通过单元层面的转换矩阵TCB得到CB 壳单元的广义弹性力及其雅可比矩阵.注意,TCB为4 个主控节点和8 个从属节点之间的转换矩阵,具体表达如下

1.2 本构关系
由连续介质力学[26]可得Green-Lagrange 应变张量的表达式

F为变形梯度张量,定义如下

式中,J=∂x/∂ξ,J0=∂X/∂ξ,X表示初始构形中任意一点的位置矢量.
将式(8)代入式(7),重写Green-Lagrange 应变张量

式中,为协变应变张量(the covariant strain tensor),定义如下

兼顾对称性和下文闭锁处理的便捷性,引入E和对应的Voigt 标记

二者之间的转换关系可表示为

式中,变换矩阵T的具体表示为

分别定义当前和初始构形中协变基矢量gi和Gi如下

将式(15)代入式(10),则协变应变的具体表示为

式中,记 (·),i=∂(·)/∂ξi,i,j取1,2,3.
采用各向同性材料的线弹性本构模型,本构关系可表示为


式中,E为杨氏模量,v为泊松比.考虑到有限元建模对象为壳结构,引入CB 壳理论中第2 个假设-平面应力条件,即 σzz=0,利用该关系式有

最终,单元本构关系可表示为

1.3 SE(3)群统一插值
与上文介绍的CB 壳单元的插值过程不同,对于SE(3)群局部标架下的几何精确壳单元,本质上是在SE(3) 群上对节点的相对运动张量H进行插值[4],其中H包含了壳单元中面节点的位置矢量和旋转矩阵,具体插值公式如下

式中,为单元任一点k和参考节点r之间的相对运动矢量,为单元节点数,为一阶Lagrange 插值形函数,为形函数的元素,expSE(3)() 为SE(3)群中的指数映射,具体表达式如下

式中,Θ为旋转伪矢量,u为在局部标架中度量的位移矢量,和TSO(3)(Θ) 分别为特殊正交群SO(3)中的指数映射和切映射.关于SE(3)和SO(3)群的基础知识参见文献[8].关于SE(3)群中几何精确壳更详细的插值过程可参见作者之前的工作[4].
注意,SE(3)群局部标架下几何精确壳单元的插值过程是在流形上完成,需要插值相对运动张量才能保证应变张量的客观性,这使得广义弹性力及其雅可比矩阵的计算比较复杂.而SE(3)群局部标架下CB 壳单元的插值过程是在 R3空间中完成,插值过程比较简单,大大简化了广义弹性力及其雅可比矩阵的计算,同时应变张量的客观性自然满足.
2 基于SE(3)群局部标架的CB 壳单元动力学平衡方程及其线性化
引入动力学平衡方程之前,先给出应变的一次和二次变分的表达式,如下

CB 壳单元动力学平衡方程的弱形式为

式中,δWint,δWine,δWLa和δWext分别为广义弹性力、惯性力、拉格朗日乘子项和外力所做的虚功.
首先,弹性力所做的虚功δWint由壳单元面内部分和剪切部分组成,经有限元离散后可表示为
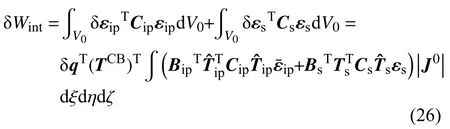

εip=和为面内应变和横向剪切应变,和为对应的协变应变,他们之间的关系可通过转换矩阵和得到[27],和来自于式(13)和式(14),具体表示为
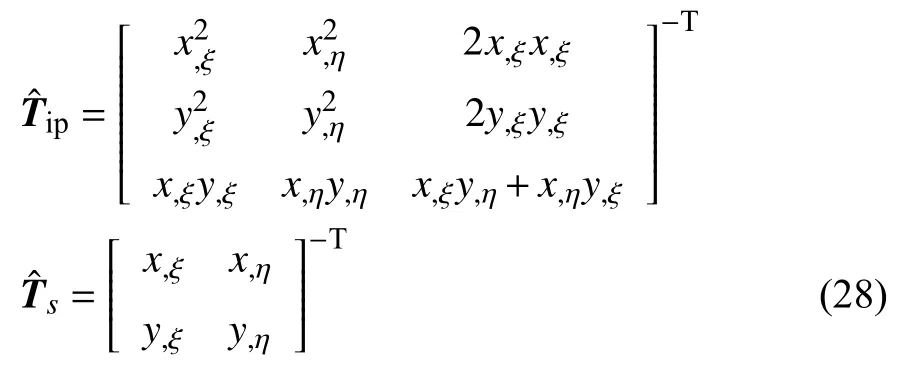
由式(26)~ 式(28)可得到广义弹性力的表达式

其中

对式(26)进一步作二次变分(即线性化)可得

式(31)中DTCB与TCB类似,具体表示为

式中,和分别为弹性力Fint在节点I处的平动和转动部分.
其次,惯性力所做虚功以及线性化过程与作者之前的工作[4]一致,此处不再赘述.
然后,拉格朗日乘子项所做虚功δWLa的具体表示为

式中L*=(G1)TR0RTg2-(G2)TR0RTg1,R0和R分别为初始和当前构形中任意一点的方向矢量相对于e3的旋转矩阵.拉格朗日乘子系数γ*的选取参见文献[4,28].注意,此处引入拉格朗日乘子项的目的是建立中面运动和drilling 自由度之间的关系,从而将5 Dofs CB 壳单元变成6 Dofs CB 壳单元.而且,其对应的弹性力和雅可比矩阵是在主控节点上计算,不需要使用TCB进行转换.此处拉格朗日乘子项对应弹性力FLa的离散形式及其线性化与作者之前的工作[4]一致,不再赘述.
最后,广义外力所做虚功δWext的离散表达式为

式中,b为外界作用的体力,n为外力作用面的法向矢量,p为作用面力大小,ρ为材料密度,Γ0为作用面积.严格地说,牛顿迭代过程中外力的雅可比也有贡献.在动力学过程中,与广义弹性力和广义惯性力的切线刚度相比,广义外力的雅可比矩阵通常可以忽略不计,故本文不再给出具体形式.
3 基于SE(3)群局部标架的CB 壳单元时间离散方法
通过上述空间离散,动力学平衡方程可表示为如下半离散形式的非线性微分代数方程组

其中,Φ和Φq分别为约束方程和约束方程的雅可比矩阵,λ为约束方程的拉格朗日乘子,t为时间,v和为系统的非物质速度和非物质加速度.
对于时间域离散,与几何精确壳类似,采用李群广义α 时间积分算法[1,29]求解上述系统动力学方程.李群广义α 方法对前后两个相邻时刻的运动增量进行差分离散,其具体离散格式可表示为

式中,αm,αf,β,γ和矢量a为李群广义α 算法参数,Δt为系统离散的时间步长,Ψn表示系统从n时刻到n+1 时刻在局部标架下的运动增量,运动张量Hn∈SE(3)包含了n时刻壳单元中面作平动和转动的全部信息.联立动力学平衡方程(37)与式(38)并采用牛顿迭代可获得下一时刻的速度vn+1和加速度,通过SE(3)群中指数映射可将运动张量Hn递推到n+1 时刻Hn+1.
4 闭锁缓解技术
4.1 基于Hellinger-Reissner 两场变分原理的闭锁缓解方法
本文采用Hellinger-Reissner 两场变分原理处理壳单元面内的闭锁,两场代表假设的位移场和假设的应力场,且两类场变量的插值相互独立.假设壳单元面内应力的分布为

式中

壳单元面内部分对应的泛函可表示为

式中,为弹性系数矩阵Cip的逆,对单元面内应变部分的泛函求变分得

进一步,对 δΠip作二次变分(即线性化)得

进一步,离散方程组可以表示为

式中,Res为残差,,Hip和Gip的表达式如下

式中βip=,静力缩聚化为单场的形式

4.2 基于ANS 的剪切闭锁缓解方法
本文使用假设自然应变 (ANS) 法缓解CB 壳单元存在的剪切闭锁.
下面构造假设应变场.如图2 所示,ANS 的核心是沿ξ和η方向在等参单元四边中点处布置采样点,通过对采样点处假设自然剪切应变线性插值得到当前构型中假设自然剪切应变,即
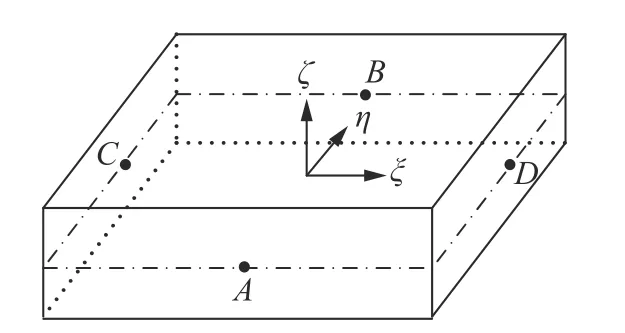
图2 ANS 插值采样点Fig.2 Interpolation sampling points for ANS


5 数值算例
本章节讨论5 个常见的静力学验证算例和一个多体系统动力学算例.为考察SE(3)群中CB 壳单元的收敛精度,下文算例中将其他壳单元的收敛结果作为参考解.其中,GESF 表示作者最近的工作-SE(3)群局部标架下经过闭锁处理的6 Dofs 一阶几何精确壳单元[4],ANCF 表示作者早期工作-基于绝对节点坐标方法的缩减(slope deficiency)板/壳单元[30],Shell181 表示有限元软件ANSYS 中的四边形壳单元[31].本部分算例的数值结果均由基于SE(3)群局部标架的6 Dofs CB 壳单元计算得到.值得一提的是,作者之前的工作[4]已经对5 Dofs 与 6 Dofs 几何精确壳单元在收敛性方面进行测试,二者收敛精度类似.区别是,SE(3)群中6 Dofs 壳单元能够完全消除刚体运动带来的几何非线性,而5 Dofs 只能部分消除.为避免重复,本节不再提供5 Dofs CB 壳的数值结果.
5.1 悬臂板末端受均布弯矩
本节考察CB 壳在大变形大转动方面的能力.
如图3 所示的悬臂板,该模型经常作为几何非线性分析的测试算例[32],长、宽和厚分别为L=12 m,B=1 m和h=0.1 m.杨氏模量为E=6.825 ×107N/mm2,泊松比为v=0.0.在悬臂板最右端施加绕Y方向的均布弯矩Mmax=2πEI0/L,其中截面惯性矩I0=Bh3/12.由图4可知,本文所提出SE(3)群局部标架下CB 壳单元计算结果与解析解吻合较好.图5给出了不同载荷下网格为20 × 2 的变形构形图.

图3 受均布弯矩的悬臂板Fig.3 Cantilever plate under the distributed moments

图4 悬臂板末端载荷-位移曲线Fig.4 Load-displacement curves at the end of the cantilever plate

图5 不同载荷下变形构形Fig.5 Deformed configurations under different loads
5.218 °开口球壳受集中载荷拉压
本节考察CB 壳单元对不可展薄壳弯曲的模拟和缓解薄膜闭锁的能力.
图6 所示为带有18°开口的球壳,该模型已成为壳单元测试的标准算例[33-34].球壳半径R=10 mm,材料的杨氏模量E=6.825 × 107N/mm2,泊松比v=0.3,厚度分别为h=0.04 (R/h=250) mm和h=0.01(R/h=1000) mm,底部受大小相等且相互垂直的一对拉力和一对压力作用,不同厚度对应的载荷大小为F=200 N (h=0.04 mm)与F=5 N (h=0.01 mm).鉴于几何对称性,只需对其1/4 结构建立有限元模型.AM和BN 为对称平面,MN和AB 为自由边.

图618 °开口球壳Fig.6 Spherical shell with an 18° hole
由图7和图8 中点A和B的位移曲线可知,当h=0.04 mm 时,12 × 12 个CB 壳单元得到收敛结果,当h=0.01 mm 时,24 × 24 个CB 壳单元得到收敛结果,验证了CB 壳单元结果的正确性.图9 给出了在最大载荷下网格数目为16 × 16和24 × 24 的两种厚度薄壳的变形构形.

图7 点A和B 位移曲线(h=0.04 mm)Fig.7 Displacement curves of points A and B (h=0.04 mm)

图8 点A和B 位移曲线(h=0.01 mm)Fig.8 Displacement curves of points A and B (h=0.01 mm)

图9 两种厚度的壳对应的变形构形Fig.9 Deformed configurations corresponding to two thicknesses of shell
将ABAQUS 中厚度为0.04 mm、网格为24 ×24 的S4 R 壳单元点A和B的计算结果PA=3.41和PB=5.88 mm 作为参考解,统计CB 壳和GESF壳不同网格的计算结果如表1 中所示,(·%)表示与参考解的误差.由此可得,与GESF 壳单元相比,CB 壳单元具有类似的收敛精度.同时,也验证了闭锁缓解技术有效改善了CB 壳单元的收敛精度.

表1 不同网格下两种壳单元在点A和B 的位移结果对比(h=0.04 mm)Table 1 Comparison of displacement results of two shell elements at points A and B under different meshes(h=0.04 mm)
图10 给出了采用16 × 16 网格时CB 壳单元和GESF 壳单元在不同载荷步(load step,LS)下牛顿迭代次数的分布.表2 中还给出了在配置处理器Intel Core i7-11700 (3.60 GHz)及32 GB 内存的PC 机Matlab 编译环境中,CB 壳与GESF 壳在收敛网格16 × 16 下弹性力及其Jacobian 矩阵的计算耗时和总牛顿迭代次数(number of iterations,NOI).尽管上述计算程序并未严格进行计算效率优化,但仿真耗时表明,由于CB 壳单元插值的简洁性,其弹性力及雅可比矩阵的计算效率远高于同阶数的GESF壳.对于0.01 mm 厚度的薄壳,可得出与0.04 mm 厚度的壳在收敛精度、牛顿迭代次数和计算时间等方面类似的结论.

图10 不同载荷步下迭代次数(h=0.04 mm,16 × 16)Fig.10 Number of iterations at different load steps(h=0.04 mm,16 × 16)

表2 不同载荷步下弹性力及其雅可比矩阵计算时间和迭代次数对比(h=0.04 mm,16 × 16)Table 2 Comparison of computational time of elastic forces and their Jacobian matrices and number of iterations under different load steps (h=0.04 mm,16 × 16)
5.3 圆柱壳中心集中受拉
本节考察CB 壳单元模拟壳结构发生以大薄膜应变主导弹性变形的能力.
如图11 所示,圆柱壳长、内径和厚度分别为L=10.35 mm,R=4.953 mm和h=0.094 mm.杨氏模量E=1.05 × 107N/mm2,泊松比v=0.3125.圆柱壳中心受集中载荷大小F=40 kN.鉴于几何对称性,只需对其1/8 结构建立有限元模型.由于该圆柱壳在拉伸过程中发生了屈曲,本文采用Lam和Morley 提出的弧长算法[35]求解平衡方程,实现平衡路径的自动追踪.由图12可得,使用24 × 16 单元网格时,CB 壳单元计算结果已经收敛,且收敛结果与GESF(24 × 16) 结果一致.可知,同等网格下CB 壳单元收敛精度与GESF 类似.图13 绘制了不同视角下圆柱壳最后的变形构形.值得一提的是,针对此算例,Zhang 等[4]曾使用SE(3)群中几何精确壳单元对此进行计算.若忽略薄膜应变中的二阶项,则直接导致点B,C的位移曲线与收敛结果之间存在较大偏差,保留此项后方可得出正确结果.因此,对于发生以大薄膜应变主导弹性变形的壳结构,使用本文提出的CB 壳单元仍然可以得出正确的数值结果.

图11 圆柱壳初始构形Fig.11 Initial configuration of the pinched cylinder

图12 点A,B和C 载荷位移曲线Fig.12 Load-displacement curves of points A,B and C
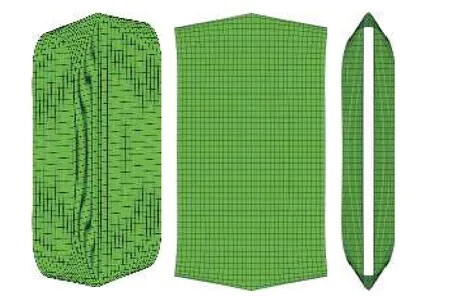
图13 三个不同视角下圆柱壳的变形构形Fig.13 Deformed configurations for cylindrical shell from three different perspectives
5.4 中心受挤压圆柱形屋顶的后屈曲分析
本节考虑图14 所示中心受挤压的圆柱形屋顶,该算例被广泛用于检验单元模拟壳结构发生屈曲变形的正确性[19,36-38].
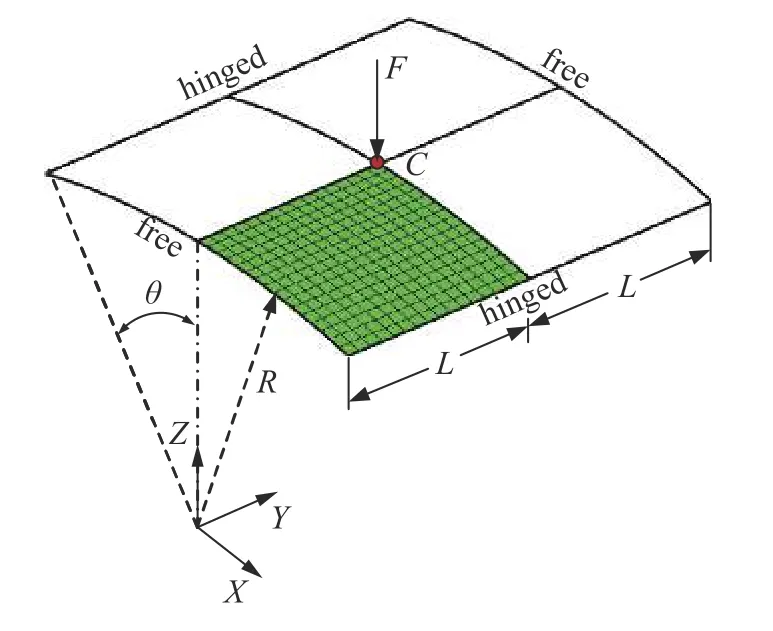
图14 中心受挤压的铰接圆柱形屋顶Fig.14 Hinged cylindrical roof subjected to a central pinching force
圆柱形屋顶边界条件为直边铰接、曲边自由,中心点C在负Z方向受挤压载荷Fmax=3000 N.杨氏模量E=3102.75 N/mm2,泊松比为v=0.3.该模型长L=254 mm,半径R=2540 mm,对应的圆心角θ=0.1 rad.鉴于几何性对称性,只需对结构的1/4 建立有限元模型.考虑两种厚度h=12.7 mm和h=6.35 mm 对结构发生屈曲变形的影响.随着载荷的增加,圆柱形屋顶在变形过程中出现突然的跳跃(snap-through)和曲率的较大变化.采用弧长法[35]计算得到点C在Z方向的位移变化如图15 所示,曲线Ⅰ和Ⅱ分别对应厚度为12.7 mm和6.35 mm 时C点的位移变化.与曲线Ⅰ相比,曲线Ⅱ中屈曲载荷相对较小,故厚度变化对结构屈曲变形有较大影响.CB 壳单元的计算结果与Sze 等[36]中使用ABAQUS中S4 R 壳单元计算结果非常一致,这说明CB 壳单元在处理发生后屈曲结构的问题时,同样表现良好.

图15 圆柱形屋顶中心的载荷位移曲线Fig.15 Load-displacement curves at the center of the cylindrical roof
5.5 直角悬臂板受均布力/力矩
本节考察CB 壳单元在处理组合体结构的数值表现,Simo 等[39]和Li 等[40]曾使用该模型检验壳单元的精度.
直角悬臂板的几何及材料参数如图16 中所示.该板右端固定,左端分别受均布力和均布力矩两种工况.λ0表示施加的均布力或均布力矩的大小.图17和图18 给出了直角板左端节点的X方向和Z方向位移变化.可知,CB 壳单元收敛结果与shell181,GESF 壳单元收敛结果吻合良好.图16 还给出了均布力和均布力矩两种工况下直角悬臂板变形构形.

图16 直角悬臂板几何、材料参数及变形构形Fig.16 Geometry,material parameters and deformed configurations of right-angle cantilever plate

图17 均布力作用下直角板左端载荷-位移曲线Fig.17 Load-displacement curves of the left end of the right-angle plate subjected to uniform forces

图18 均布力矩作用下直角板左端载荷-位移曲线Fig.18 Load-displacement curves of the left end of the right-angle plate subjected to uniform moments
5.6 空间薄圆柱壳双摆多体系统动力学
本节通过一个空间薄圆柱壳双摆模型的多体系统动力学仿真考察CB 壳单元在动力学过程中描述大变形和刚体位移以及消除几何非线性方面的表现,Liu 等[30]、Shi 等[41]曾研究该模型在重力作用下的动力学响应.
如图19 所示,曲面ACEFDB 由平面I和II 将两个半径均为0.3 m 的圆柱壳裁剪形成,裁剪平面I和II 与平面XOZ之间的夹角满足关系tanθ=0.5.圆柱壳Y方向长度为1.2 m,厚度为0.01 m,杨氏模量为E=1.0 × 109Pa,材料密度为7810 kg/m3,泊松比为0.3.圆柱壳I 左端AB 简支,圆柱壳I和II 通过沿Y轴方向的CD 边圆柱铰接.重力加速度为9.81 m/s2,总仿真时间为1.5 s.本算例中,牛顿迭代收敛标准设为广义坐标修正量‖Δ‖2<1.0 × 10-6.

图19 由两个圆柱壳组成的空间双摆模型Fig.19 A double pendulum composed of two parts of cylindrical shells
首先,通过与作者早期工作中基于ANCF 的壳单元[30]对比,验证SE(3)群局部标架下CB 壳单元描述动力学问题的正确性.图20 为不同单元数量下点F在Z方向的位移变化.当每个壳单元网格数目为15 × 15 时,该模型计算结果与ANCF 壳单元数值结果吻合良好,验证了动力学仿真过程中CB 壳单元的收敛精度.若以图19 中圆弧AC和CE 的长度变化分别作为两个圆柱壳发生弹性变形的度量,变形率即为当前和初始构形中两弧长之差与初始构形中弧长的比值,变形率为负数时表示当前构形中的弧长小于初始构形的弧长.在1.5 s 仿真过程中,圆柱壳I和II 的最大变形率可达58%和30%.图21给出了网格数目为25 × 16 下双摆圆柱壳在不同时刻的构形图,可以看出该模型发生了较大的变形和刚体位移.

图20 不同单元数目下点F 在Z 方向的位移曲线Fig.20 Displacement curve of point F in Z-direction with different number of elements

图21 双摆变形构形Fig.21 Deformed configurations of the double pendulum
其次,通过分析系统质量矩阵和切刚度矩阵更新情况验证SE(3)群中CB 壳单元能够有效降低刚体运动带来的几何非线性.若忽略广义外力的雅可比矩阵,系统迭代矩阵的具体表示为

其中,M和K分别为系统的广义质量矩阵和切刚度矩阵.表3 记录了总仿真时间的前1 s 双摆模型的迭代矩阵主要部分Jq=Δt2β(M+K) 的更新次数(number of update,NOU)和圆柱壳在双摆过程中牛顿迭代总次数NOI.“NNI≥i”表示在一个时间步内,若牛顿迭代的次数大于等i,则矩阵Jq强制更新.“Frozen”表示系统从初始构形计算得到矩阵Jq之后不再更新.

表3 迭代矩阵更新次数及牛顿迭代总次数(E=1.0 GPa)Table 3 The number of times that the iteration matrix is updated and the number of total Newton iterations (E=1.0 GPa)
表3 的数值结果表明:以时间步长为5.0 ×10-4s 工况为例,当Jq矩阵在每个牛顿迭代步更新时,需要更新的次数为7022.当NNI≥3 时(即每个时间步长中牛顿迭代次数等于或超过3 步时更新一次Jq矩阵)总牛顿迭代次数增加了5.5%,Jq矩阵的更新次数下降了78.9%.图22 给出了系统Jq矩阵更新次数的分布以及圆柱壳I和II 的变形率变化曲线,可知在0.357 s 时Jq发生了第一次更新,这段时间主要以圆柱壳I 的变形为主,此时圆柱壳I和II 的变形率约为33%和0.4%.0.357 s 至0.408 s 期间Jq不需要更新.直至0.409 s 发生了第二次更新,此时圆柱壳I和II 的变形率约为52%和2%.从0 s 至0.409 s 期间,双摆模型变形率的变化基本保持平稳.0.409 s 之后,Jq在每一个时间步更新的次数和频率有所增加,这是由于圆柱壳I和II 在发生相对较大变形的同时变形率出现了较大的波动所致.事实上,在仿真计算中,每个物体甚至每个单元可以根据当前的变形程度自适应的选择是否更新单元的广义质量矩阵和切刚度矩阵,其鲁棒性的判断标准值得进一步研究.

图22 Jq 更新次数分布及圆柱壳的变形率曲线Fig.22 Distribution of the number of times that Jq is updated and curves of deformation rate of cylindrical shells
若考虑较小时间步长的工况,此时系统的迭代矩阵中广义质量矩阵的占比提升.通常,柔体的广义质量矩阵与系统的弹性变形相关,而切刚度矩阵与系统弹性变形的梯度相关.与切刚度矩阵相比,广义质量矩阵变化较小.因此,时间步长为1.0 × 10-4s时,总牛顿迭代次数仅增加了2.4%,Jq矩阵更新次数下降了98.8%.与总迭代次数相比,Jq矩阵的更新次数基本上可以忽略不计.
若将上述模型中杨氏模量设置为1.0 × 1011Pa,其余参数保持不变,与表3 类似,表4 记录了该杨氏模量下Jq的更新次数和牛顿迭代总次数.考察时间步长为1.0 × 10-3s 时的工况,当Jq矩阵在每个牛顿迭代步更新时,需要更新的次数为2972.当系统出现Frozen 现象时,总牛顿迭代次数增加了8.8%,Jq矩阵不需要更新.

表4 迭代矩阵更新次数及牛顿迭代总次数(E=100 GPa)Table 4 The number of times that the iteration matrix is updated and the number of total Newton iterations (E=100 GPa)
由上述数值结果可知,基于SE(3)群局部标架的CB 壳单元继承了李群局部标架方法体系下非线性有限单元(如基于SE(3)群局部标架的几何精确梁单元、基于SE(3) 群局部标架的几何精确壳单元)的优势[1],即在计算中消除了刚体运动带来的几何非线性,使动力学系统的广义惯性力、广义弹性力及其雅可比矩阵满足刚体运动的不变性.
值得一提的是,在多体系统求解过程中,除减小质量矩阵及切线刚度矩阵更新次数外,如何有效利用上述性质提高线性方程组的直接解法或迭代算法的计算效率仍值得进一步探索.
6 结论
本文融合李群局部标架方法和经典CB 壳理论开发了基于SE(3)群局部标架的CB 壳单元.从单元计算角度看,广义弹性力及其雅可比矩阵的线性化过程不需要复杂的插值运算和变分操作,大大简化了广义弹性力及其雅可比矩阵的计算过程,而且不需要使用相对插值即可保证插值算法的客观性和路径无关性.从几何非线性角度看,该单元继承了李群局部标架方法体系中非线性有限单元(如SE(3)群局部标架下的几何精确梁单元、几何精确板/壳单元) 的优势,即消除了由刚体运动带来的几何非线性,广义惯性力、广义弹性力及其雅可比矩阵满足刚体运动的不变性.从收敛性角度看,闭锁缓解技术有效改善了SE(3)群局部标架下CB 壳单元的收敛精度,使得CB 壳单元与GESF 壳单元在收敛精度方面类似,具有渐进二阶收敛率.从计算时间角度看,与GESF 壳单元相比,CB 壳单元在计算效率方面具有较大提升.此外,对于组合体结构,例如壳与壳连接结构,含有drilling 自由度的CB 壳单元可直接进行处理.
借鉴上述基于SE(3)群局部标架的CB 壳单元的研究思路,后续可融合李群局部标架方法与基于连续体的梁理论,展开基于SE(3) 群局部标架的CB 梁单元的相关研究工作,实现对SE(3)群中几何精确梁单元插值过程的简化.进一步,可在上述研究基础上,结合共旋坐标法(Co-rotational formulation,CRF)[42-45]的建模思想,提出基于SE(3)群的共旋CB 梁单元和CB 壳单元,可进一步提高计算效率.

