泊松方程的广义有限差分方法

李 瑞

(陕西师范大学 数学与统计学院，西安 710119)

随着计算机的不断更新和数值方法的快速发展,科学计算应运而生,研究在计算机上运行的数值算法的构造及其数学理论的偏微分方程数值解得到了前所未有的发展.科学计算融合数学建模、数值算法、软件研发和数值模拟等手段来认识和解决复杂的具有实际应用背景的科学工程问题，是计算机实现其在高科技领域应用的必不可少的纽带和工具.[1]

泊松方程的一般形式为：

它可以描述静电场、静磁场的分布、稳定温度场、稳定浓度场的分布. 在定解问题、定解条件以及解的物理分析教学过程中增加相关的工程背景及实用性，激发学生的学习兴趣．如针对解光滑连续的性质，介绍其在图像处理除噪过程中的应用，使学生对其有直观的印象和更深入的理解．针对地下油气水的渗流问题，讲授压力传导方程的导出及如何写出定解条件．通过有针对性的讲授，提高学生提出问题、分析问题和解决问题的能力．[2]

1 二维泊松方程的有限差分方法

针对二维泊松方程，对矩形区域进行网格剖分如图1所示.

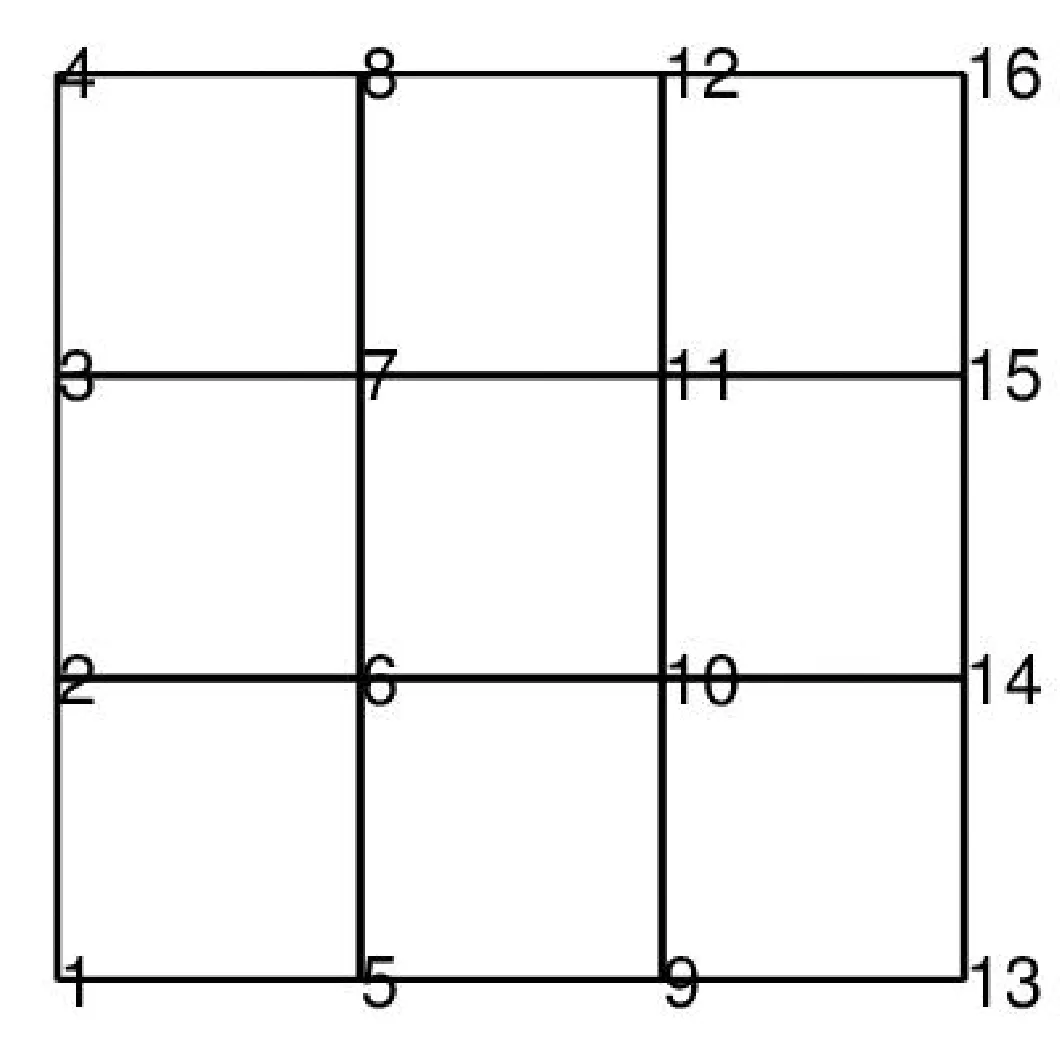
图1 矩形网格剖分

记ui±1,j=：u(xi±Δx,yj),ui,j=：u(xi,yj),ui,j±1=：u(xi,yj±Δy),利用Taylor级数展开可得偏导数：

则二维泊松方程的有限差分格式为：

由于差分格式中只出现在u(xi,yj)及其相邻的四个点处的值，故称为五点差分格式.但随着问题的复杂，对拟真性的要求越来越高，传统的差分方法会受到计算区域边界形状及网格剖分的限制.[3]

2 二维泊松方程的有限体积方法

针对矩形网格剖分和三角形网格剖分，沿着差分方法中微分算子的离散思想，引入原始网格剖分的外心对偶体，如图2所示.根据格林公式

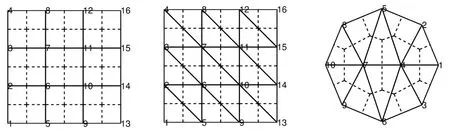
图2 网格剖分及其外心对偶体单元

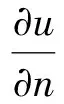
对二维泊松方程两边同时乘以1，利用格林函数可得：

若对偶体是矩形网格，沿其四边的线积分用中矩形公式替代，可得：

利用一点高斯积分，可得二维泊松方程的有限体积离散格式：

注意到，建立在矩形对偶体上的数值格式与五点差分格式完全相同.

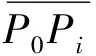
可得P0处的有限体积格式：

三角形网格剖分的外心对偶体受到网格剖分的影响，如一致三角形网格的外心对偶体是矩形网格，非一致网格剖分有可能构造不出来，如钝角三角形.

3 二维泊松方程的广义有限差分方法

图3 三角形单元及其外心对偶体(左图)和重心对偶体单元(右图)

对二维泊松方程两边同时乘以1，在对偶体单元上利用格林函数可得：

通过数值积分，可以建立以网格节点上的值为自由度的代数方程组，从而把泊松方程的定解问题转化为求解代数方程组的问题.重心对偶体对一致三角形网格剖分、非一致三角形网格剖分和复杂计算区域都有很好的适应性，如图4.

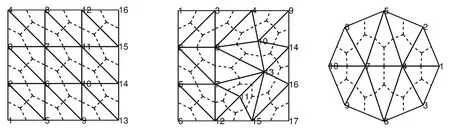
图4 三角形网格剖分及其重心对偶体单元

对于二维泊松方程，从上述可看出：

(1)矩形网格剖分的外(重心)心对偶体亦是矩形网格，有限体积离散格式等价于五点差分格式；

(2)三角形网格剖分的外心对偶体会受到原始网格剖分的影响，有限体积离散格式可直接利用一点高斯积分公式直接给出；

(3)三角形网格剖分的重心对偶体具有普遍适用性，有限体积离散格式通过格林公式得到，刚度矩阵可以通过数值积分得到.

4 结语

综上所述，无论是外心对偶体，还是重心对偶体，自由度都是定义在网格节点上，此类方法可以看作特殊的有限差分方法，称之为广义有限差分方法.[6]给出的基于重心对偶体的有限体积离散格式，同样适用于传统有限差分离散格式和基于外心对偶体的有限体积离散格式.此格式具有形式上的统一性，这有利于学生们的理解和掌握，从而提高学生学习和应用有限差分方法的兴趣．