一类具有强偶圈分解的4-正则线图

王丹丹

(南京航空航天大学 理学院，南京 211106)

1 介绍

本文考虑的图都是有限图，它可以含有平行边，但不含自环．对于一个图G，用V(G)和E(G)分别表示图G的点集和边集．用L(G)表示图G的线图，其中：L(G)中的两个点连m(m≤2)条边当且仅当G中对应的边有m个公共端点．文中没有定义的概念和术语参见文献[1]．

我们知道，一个连通图是偶圈可分解的必要条件是它是欧拉图而且有偶数条边，反之是不成立的，例如：K5是一个有10条边的4-连通4-正则图，它是欧拉图但没有偶圈分解．在1981年Seymour[2]证明了每个2-连通欧拉平面图是偶圈可分解的；在1994年Zhang[3]证明了2-连通K5-minor-free欧拉图是偶圈可分解的．在2017年，Huynh在文献[4]中提出强偶圈分解的概念：如果一个图的任何一个具有偶数条边的细分，都有一个偶圈分解，则称该图是强偶圈分解的．根据强偶圈分解的概念很容易证明Seymour和Zhang的结果也是强偶圈分解的．Huynh[4]还证明了完全二部图Km，n(m，n都是偶数)是强偶圈可分解的，进一步推出几种特殊图是强偶圈分解的．

Ash和Jackson[5]猜想：每个圈4-边-连通立方图有一个控制圈．文献[6]中已证明：每一个有控制圈的2-连通立方图线图是强偶圈分解的．若这个Ash和Jackson猜想正确，则表明每个圈4-边-连通的立方图的线图是强偶圈分解的．本文推广了文献[6]中结果，证明：对2-连通立方图G，它存在一个圈C使得G-V(C)是一个森林，则L(G)是强偶圈分解的．

下面，我们列举本文中经常会用到一些定义、引理及定理．

一个符号图(G，Σ)就是由图G和一个符号集Σ⊆E(G)组成的图，其中符号集Σ中的边称为符号边，不在符号集Σ的边称为非符号边．在符号图中，若一个圈有奇数条符号边，则这个圈称为奇符号圈，否则称为偶符号圈．

对X⊆V(G)，δG(X)是无自环的边集且每条边有且仅有一端在X中，则称δG(X)是X的导出割．若两个符号集Σ1，Σ2⊆E(G)的对称差Δ是一个割，则称Σ1，Σ2是等价的．注意：符号等价是一种等价关系．若Σ1，Σ2⊆E(G)是等价符号，则符号图(G，Σ1)和(G，Σ2)具有完全相同的偶圈集．因此，如果Σ1和Σ2是等价的，则符号图(G，Σ1)是偶圈分解的当且仅当符号图(G，Σ2)是偶圈分解的．

定义1[4]一个图G是强偶圈分解的当且仅当对E(G)中任意符号集Σ，当|Σ|为偶数时，则对应的符号图(G，Σ)是强偶圈分解的．

定义2[6]链H是由首尾相连的一串2-圈{c1，c2，…，cn}组成的，其中任意相邻2-圈ci与ci+1只有一个交点，1≤i≤n-1，如图1所示．

图1链

定义3[6]次链是从链H任意选择一条边细分一次．

定义4[6]若H是任意哈密顿立方图，C是H中哈密顿圈．设H中的点集标为x1，…，xn，y1，…，yn(n≥1)，且C的所有弦集为{x1y1，x2y2，…，xnyn}．对每个i=1，2，…，n，用链Hi代替xi与yi之间弦xiyi(Hi的边是任意大)，产生的4-正则图称为链弦图，记为G，如图2所示．

定义5[6]若H是任意哈密顿立方图，C是H中哈密顿圈．设H的点集标为x1，…，xn，y1，…，yn(n≥1)，且C的所有弦集为{x1y1，x2y2，…，xnyn}．令C*表示将C恰好细分一次，将弦x1y1替换为x1和y1之间次链H1，并将C*中唯一2度点和H1中唯一2度点结合记为点z．进一步，用链Hi代替xi与yi之间弦xiyi(i=2，…，n)(Hi的边是任意大)，产生的4-正则图称为次链弦图，记为G，如图3所示．

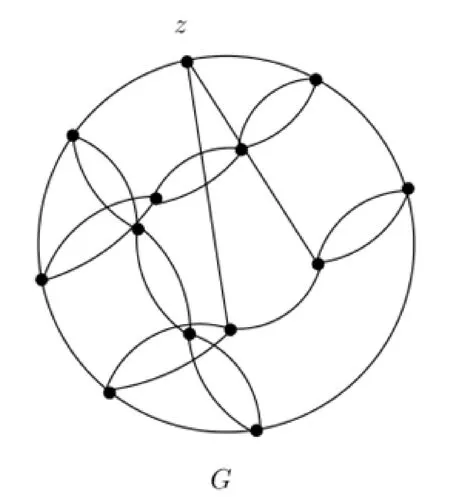
图3 次链弦图

下面一些引理将贯穿整个证明过程．

引理1[7]设(G，Σ)是一个符号图，对任意不含圈的边集F⊆E(G)，存在一个符号ΣF与Σ等价，使得ΣF∩F=∅.

引理2[2]每个2-连通欧拉平面图是强偶圈分解的．

引理3[6]每个链弦图是强偶圈分解的．

引理4[6]每个次链弦图是强偶圈分解的．

定理1[6]若图G是哈密顿立方图，则L(G)是强偶圈分解的．

2 立方图线图的偶圈分解

在证明主要结论之前，先证明两类特殊的4-正则图是强偶圈分解的．

若G1是任意链弦图，{x0y0，x1y1，x2y2，…，xpyp}为G1的链集，C为链弦图的外圈，令C*表示将C细分n次，用链xy代替G1中链x0y0，其中链xy是由m个2-圈组成的，任意选择其中n(2≤n≤m)个2-圈，将这n个2-圈各选择一条边细分一次，并将C*中n个2度点与链xy的n个2度点一一结合，记为点vi．进一步，规定从x到y的顺时针方向依次记为v1，v2，…，vk，…，vn，与之对应的三角形记为D1，D2，…，Dk，…，Dn，产生的4-正则图称为广义次链弦图，记为G，如图4所示．

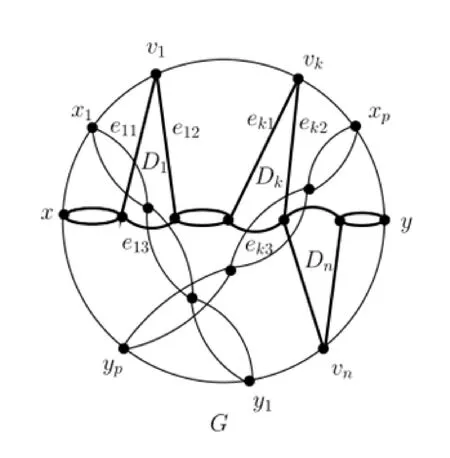
图4 广义次链弦图

定理2每个广义次链弦图是强偶圈分解的．

证明设图G是以上描述的广义次链弦图，设Σ⊆E(G)是任意一个符号且|Σ|为偶数，要证明G是强偶圈分解的，只需要证明(G，Σ)是偶圈分解的．

将三角形Di与vi关联的边分别记为ei1，ei2，Di第三条边记为ei3．如果D1，D2，…，Dk，…，Dn中至少有一个奇符号三角形，不失一般性，不妨令第一个奇符号三角形为Dk．如果Dk不存在，说明D1，D2，…，Dk，…，Dn均为偶符号三角形．

首先，对每个i≠k，用v′i，v″i替换Di中vi，使得v′i∩C≠∅，v″i∩C=∅，且保证替换后得到的图与原图的对应边符号保持一致，由于替换后的图会出现2度点，进一步，收缩图中所有2度点，得到图G′，如图5所示．通过上述操作可以知道G′为次链弦图．需要注意的是：当Dk不存在时，则G′为链弦图，因此由引理3或引理4可知，G′是强偶圈分解的．

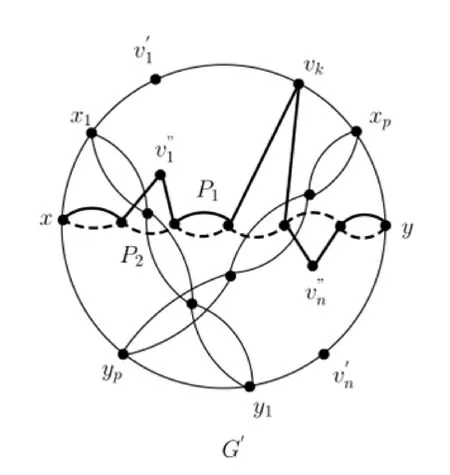
图5 图G中用v′i，v″i替换Di中vi后并收缩2-点

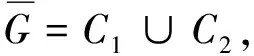
对每个i≠k，如果v′i，v″i同时含在C1(或C2)上，那么在C1(或C2)中会出现4度点，令满足上述条件的点集为V，集合V中点vi关联三角形Di的集合记为T．此时作C1、C2与T的对称差，记C1ΔT=C′1，C2ΔT=C′2．

情况1当C′1，C′2为偶符号圈时，由于已经通过对称差将圈中所有形成闭路的4度点转化为2度点，因此，图G的偶符号圈集为{C′1，C′2，C3，…，Cs}．

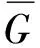
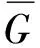
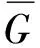
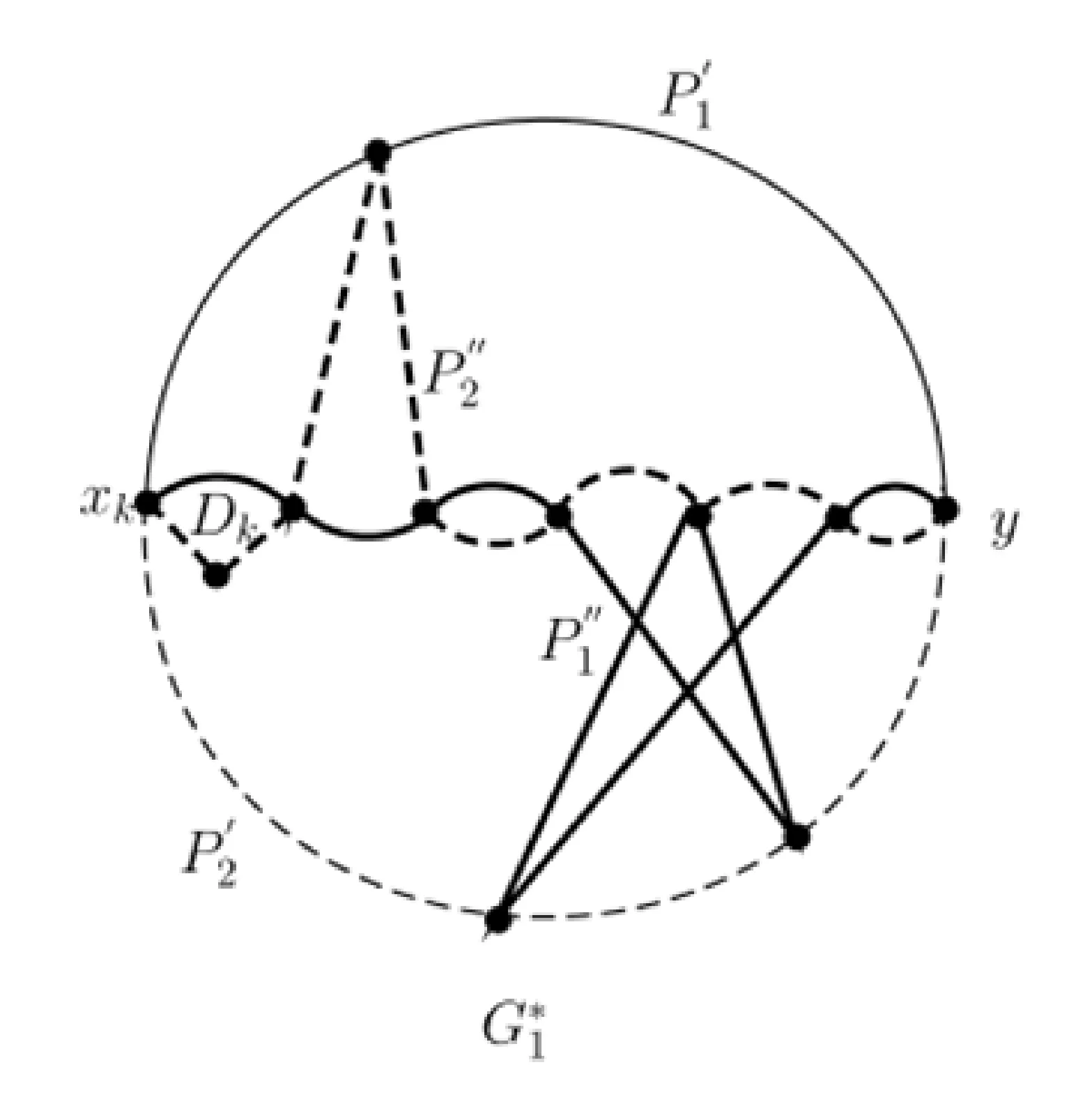
图6 点x与Dk之间偶符号2-圈及偶符号三角形独自偶圈分解后剩余图

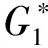
通过以上讨论可推出G是强偶圈分解的，结论成立．[8]

若G1是任意链弦图，{x0y0，x′1y′1，x′2y′2，…，x′ny′n}为G1的链集，C为链弦图的外圈，令C*表示将C细分i次，用链xy代替图G1中链x0y0，其中链xy中每个2-圈均选择其中的一条边细分一次，且将链x′iy′i(i=1，…，j，j≤n)用次链xiyi替换，并将链xy中i个2度点与C*中2度点一一结合，记为点qi，链xy中剩下2度点分别与链xiyi中2度点一一结合，记为点vi，得到的4-正则图称为泛次链弦图，记为G，如图7所示．

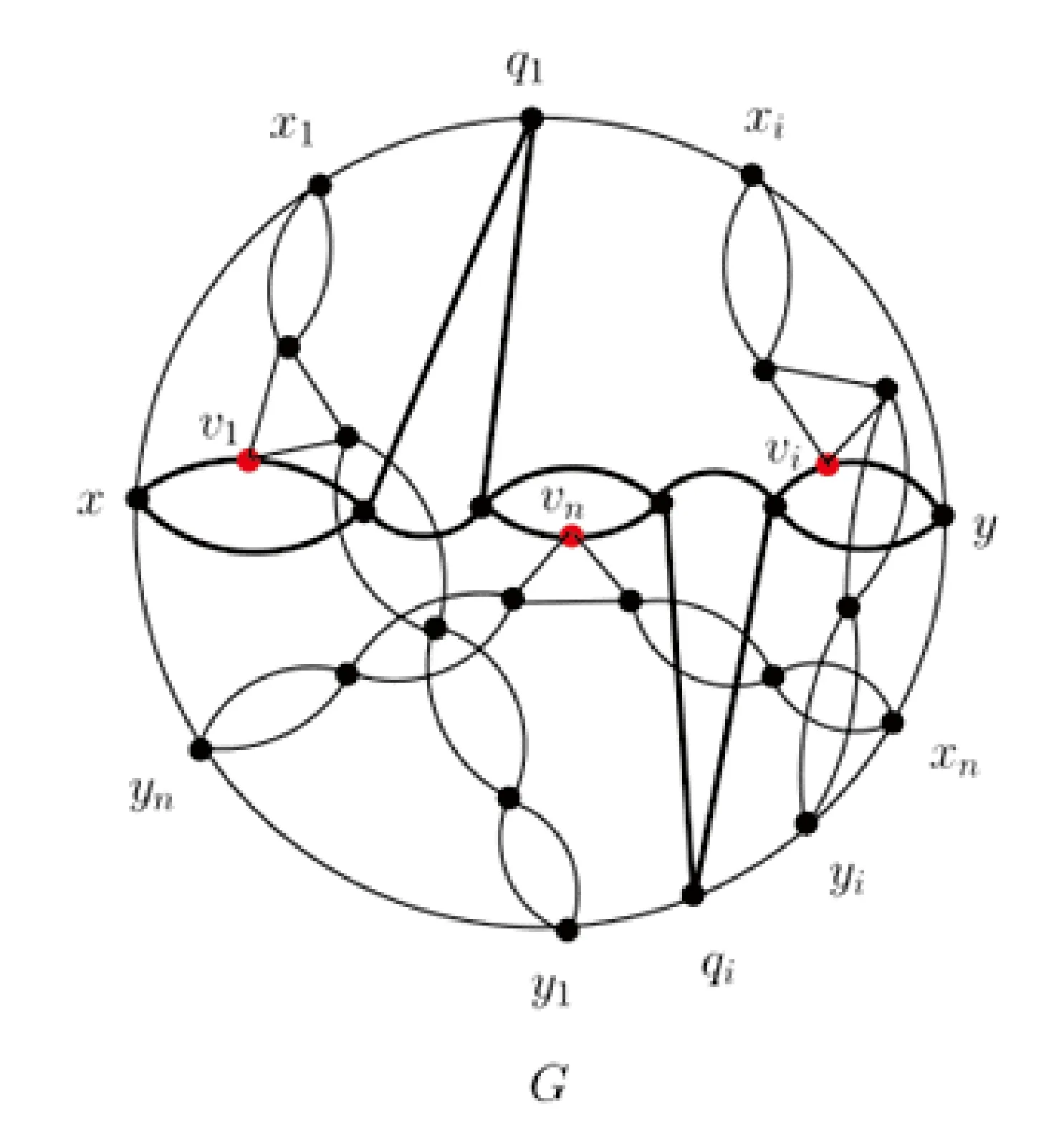
图7 泛次链弦图

定理3每个泛次链弦图是强偶圈分解的．

证明设图G是以上描述的泛次链弦图，设Σ⊆E(G)是任意一个符号且|Σ|为偶数，要证明G是强偶圈分解的，只需要证明(G，Σ)是偶圈分解的．

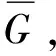
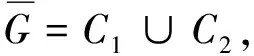
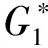
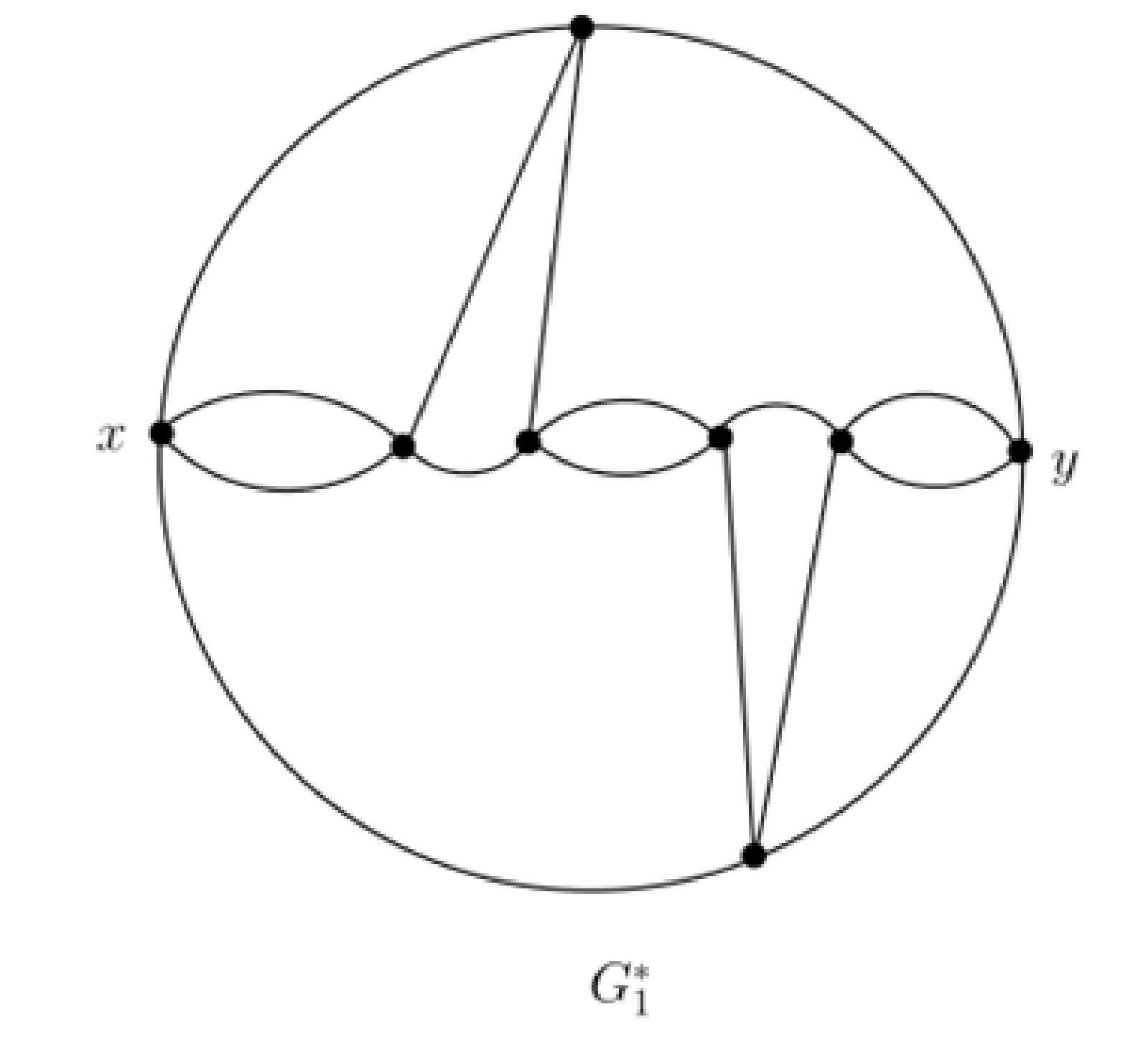
图8 只含链xy

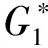
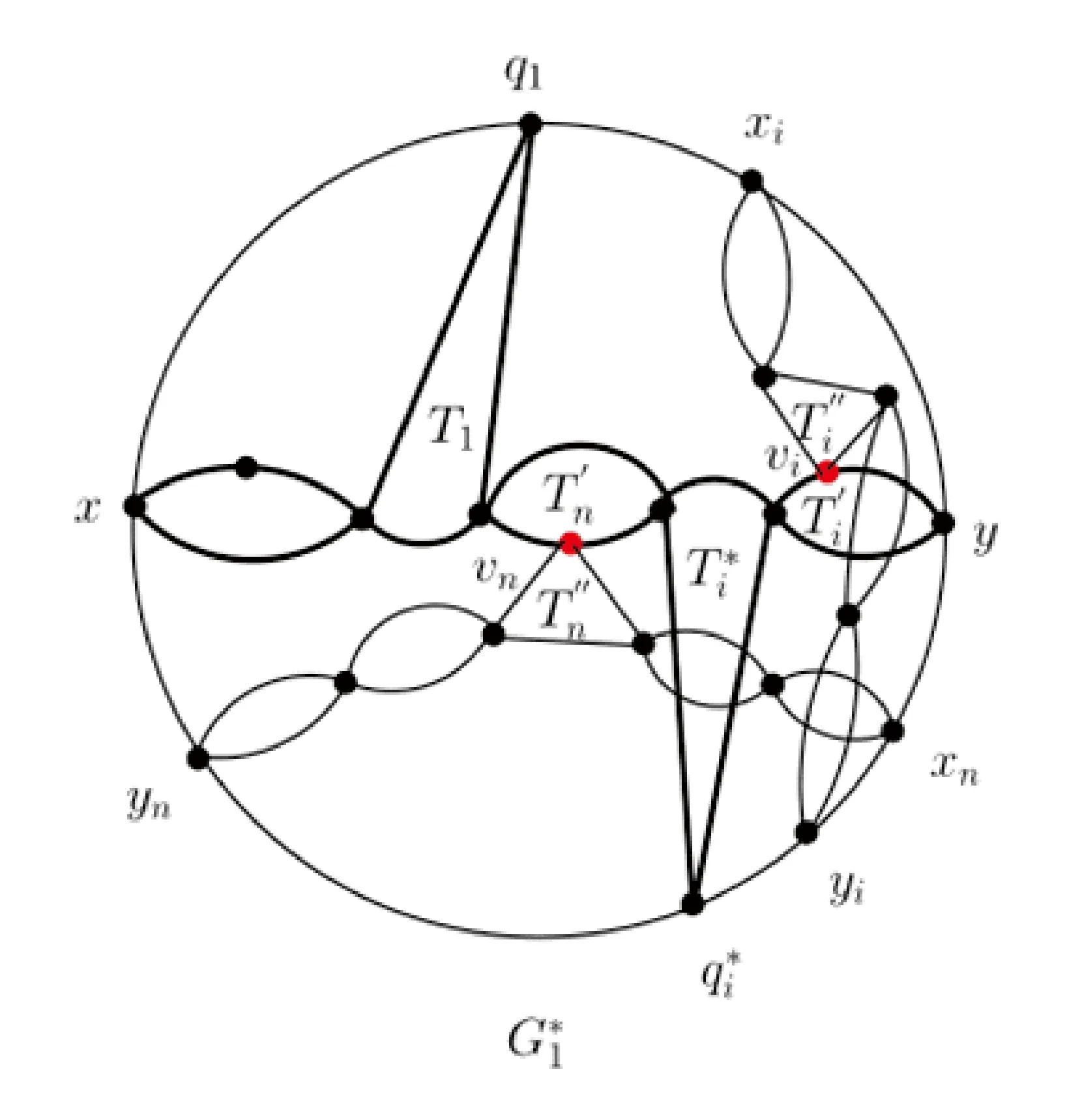
图9 含链xy和链xiyi，i=1，2，…，t2(t2≤n)

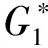
情况1当|P1|+|Q1|为偶数时，只需要令

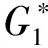
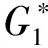
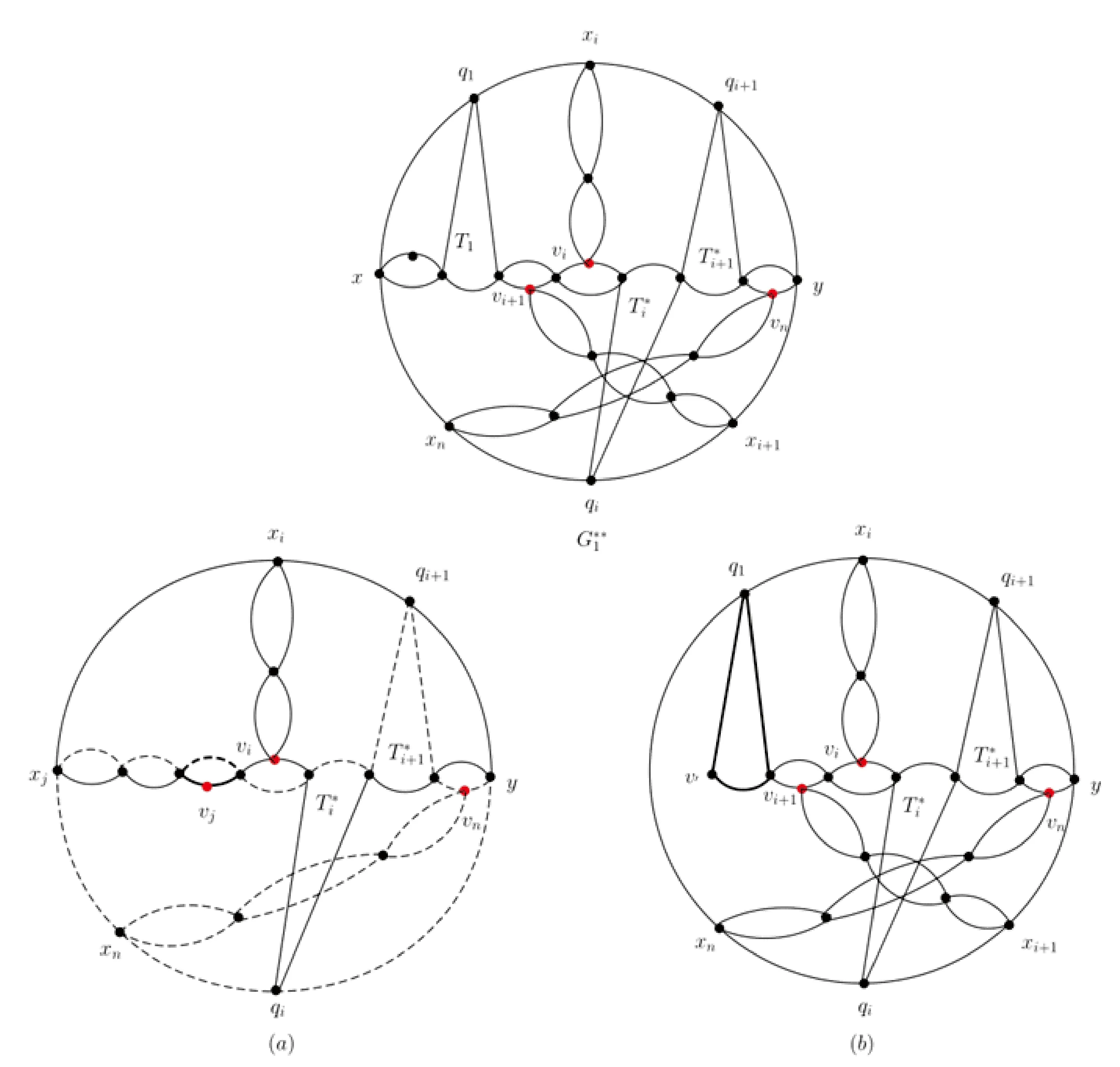
图10 第一个vj关联三角形符号为奇第一个三角形Ti符号为奇

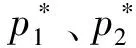
因此可推出图G是强偶圈分解的，结论成立．

定理4对2-连通立方图G，如果它存在一个圈C使得G-V(C)是一个森林，则L(G)是强偶圈分解的．

证明在(L(G)，Σ)中|Σ|为偶数．首先找出图G的外圈C，那么外圈C的线图将会形成两个圈分别记为C1、C2，接下来考虑G-V(C)的线图，在G-V(C)中任意选择两端点均在外圈C的路P1，将它的线图L(P1)与C1结合，进一步，将两个端点均在外圈C的路P2，其中L(P2)与L(P1)是相邻的，将L(P2)与C2结合，紧接着，将两个端点均在外圈C的路P3，其中L(P3)与L(P2)是相邻的，将L(P3)与C1结合.以此类推，交替结合，直到最后一条路Pn的线图L(Pn)，这样L(G)将由两部分组成，如图11所示的粗实线和粗虚线．

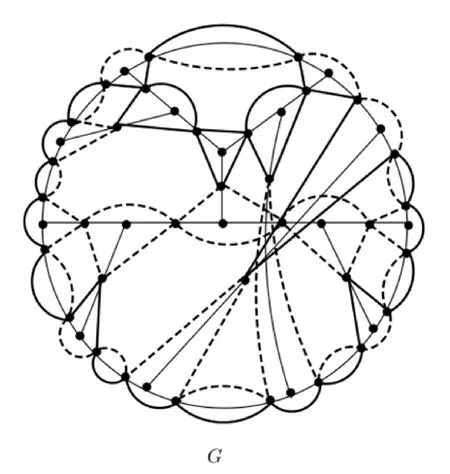
图11 图G的线图分解成两个子图

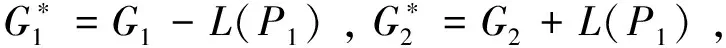
因此L(G)是强偶圈分解的，结论成立．