从数系扩充认知指数函数的概念

孙德荣 高全祖 刘 雪

（1.昌吉学院数学与数据科学学院 新疆 昌吉 831100；2.昌吉州第一中学 新疆 昌吉 831100）

函数是大学数学专业数学分析课程的研究对象，基本初等函数幂函数、指数函数、对数函数又是中学数学教学的一个重要内容，指数函数作为高中生学习函数的开始，对后续函数的学习起着基础性的作用，它是将幂指数从整数范围扩充到实数范围之后，建立的第一个重要的基本初等函数。我国现行的中学数学教材一般是从数系的扩张出发来构建数学运算的，学生对指数函数的认知也是从正整数集到实数集内的幂指数运算开始的。数学师范生在完成数学学科专业课学习之后，已经具备了足够的学科知识，可以从数系扩张的角度来重新认识与完善指数函数的相关知识体系，以提高自身的专业与学科核心素养，更好的指导中学数学教学。［1］

1 有理数域内幂指数运算的建立与完善

对指数函数的认识关键在于对幂指数概念的构建与运算性质的理解，随着学生对自然数、整数、有理数、实数和复数等相关数系知识的逐步认识，在不同的学习阶段对幂指数的概念与性质也逐步得到完善，最后形成了较为完整的指数函数概念。

这里全体非负整数的集合称自然数集，用字母“N”来表示，包含正整数和零；N+表示正整数集；Z表示整数集；Q表示有理数集；R表示实数集；C表示复数集。

1.1 整数集内幂指数概念的建立

中学数学教材［2］由几何意义出发，从一个数的平方、立方，引导学生认识了一个数的n次方的整数幂的概念与性质。即

一个数a与它自身的乘积叫做这个数的平方（或二次方），记作a×a=a2，例如，在几何中，边长为a的正方形的面积为S=a×a=a2。

三个相同的数a的乘积叫做这个数的立方（或三次方），记作a×a×a=a3，例如，在几何中，棱长为a的立方体的体积为V=a×a×a=a3。

n个相同的数a的乘积叫做a的n次方，记作a×a×…×a=an。an也称为a的n次幂，其中a叫做底数，n叫做幂指数，这里n∈N+。

利用幂的概念以及乘法与除法的意义，容易推导出正整数指数幂的运算法则：

法则1：am·an=am+n(m,n∈N+)；法则2：法则3：(am)n=amn；

法则4：(a·b)n=an·bn；法则5：a0=1(a≠ 0)。

在整数范围内，初中生学习乘法的意义之后，又有了相应的负整数幂和零指数幂的规定，幂的运算性质的逻辑推理也就完善了。中学数学教材通过以上方式给学生建立了整数幂的严密逻辑体系。

1.2 幂指数运算在有理数域内延拓

现行人教版普通高中课程标准实验教科书［3］在引入了根式运算之后，就将幂指数概念扩展到了有理数域范围内。

首先教材［4］给出根式的意义：一般地，如果xn=a，那么x叫做a的n次方根，其中n＞1，并且n∈N+。当n是奇数时，正数的n次方根是一个正数，负数的n次方根是一个负数，表示为。当n是偶数时，xn=a是一个正数，正数a的n次方根有两个，这两个数互为相反数，表示为。其中，式子叫做根式，n叫做根指数，a叫做被开方数。

其次教材［5］从几个特殊的实例出发，如：探究归纳分数指数幂的运算规律，给出如下定义：

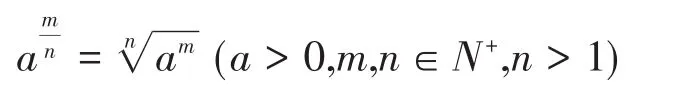
另外，1）对负分数指数幂给出了与负整数指数幂相仿意义的规定：

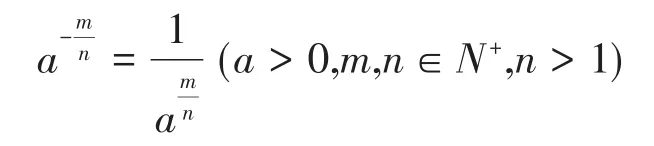
2）规定0的正分数指数幂为0，0的负分数指数幂没有意义。

以上规定将整数指数幂的概念推广到了有理数域。

最后教材［6］给出结论：整数指数幂的运算性质对于有理数指数幂也同样适用，即

（1）aras=ar+s(a＞ 0,r,s∈Q);

（2）(ar)s=ars(a＞ 0,r,s∈Q);

（3）(ab)r=arbr(a＞0,b＞0,r∈Q).

存在的问题是教材并未对定义的合理性（当m不能被n整除时）与运算性质的正确性给予说明或证明（教材的编写缺乏逻辑严密），如果教师在教学中也如同教材一样一带而过，那就会造成学生认知结构上的逻辑缺失。按照高中生现有的认知水平，运算性质（1）—（3）是可以证明的。事实上，对运算性质的证明，也就是对定义合理性的有力佐证。

为了证明有理数指数幂的运算性质，要补充证明以下三个性质：

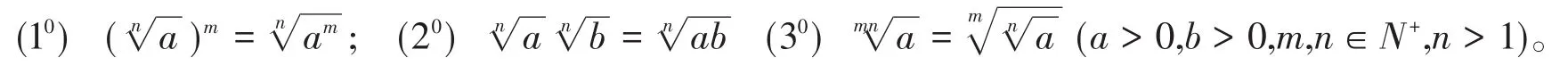
性质（10）—（30）也并不是显然的，证明如下：

证明 设a＞0,b＞0,∀m,n∈N+,n＞1.

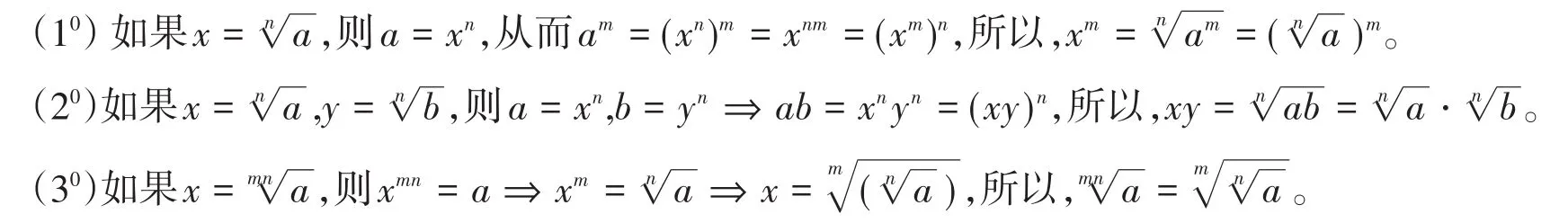
根据分数指数幂的定义以及性质（10）—（30），对性质（1）—（3）的证明如下：

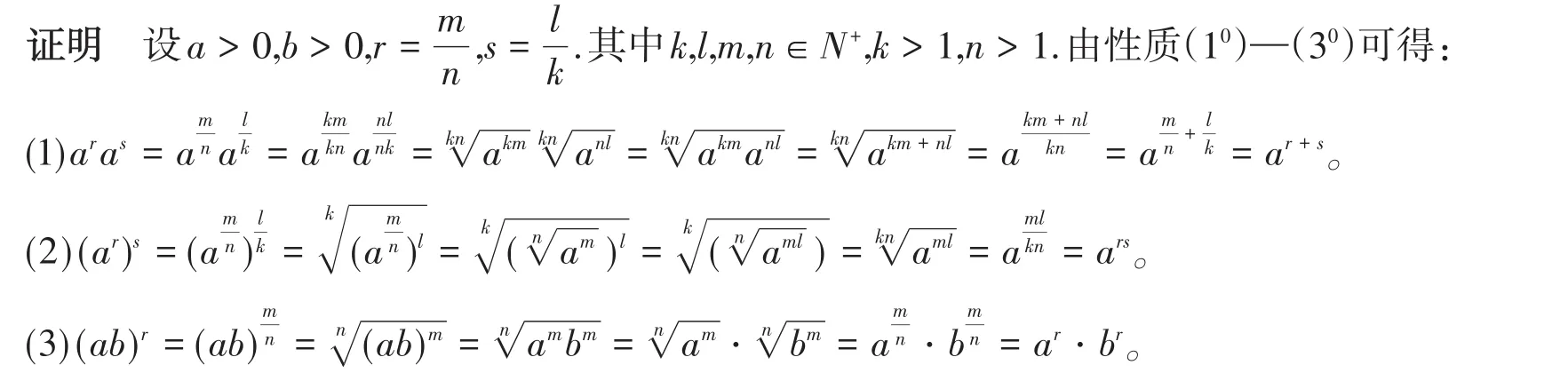
从以上推理可以看到，有理数指数幂的性质并不是显然的。在学生已有的认知水平上，通过推理证明自然得到分数指数幂的性质，既说明了定义的合理性又完善了知识结构的逻辑严密性。这样，幂指数运算在有理数域内的延拓就没有什么遗憾了。

2 实数域内指数函数概念的建立与完善

对于a＞0(a∈R)来说，任意一个有理数x都满足一个与它对应的有理指数幂ax＞0，这样就能够把整数指数运算扩展到有理指数幂的运算。我国现行的高中数学教材中［7］直接给出了实数域内指数函数的概念：一般如y=ax（a＞0，且a≠1）的函数叫做指数函数，函数的定义域是R。这里如果x为有理数，那么学生根据有理数幂指数的运算知道函数值ax的意义，但是当x为无理数时，ax的意义为何？之前学生并没有认识，高中教材采取了以一个特例的实验观察法告诉学生，对任意一个无理数x，ax都唯一对应一个实数，这是高中数学在实数域内介绍指数函数的逻辑不严密所在。

大学数学在建立了实数极限理论的相关知识和概念之后，就可以完善指数函数在实数范围内的定义。首先大学数学专业的数学分析课程中，通过级数理论可以建立有理数与无理数之间的运算。

由上述命题可知，如果a0.a1a2…an…是一个无理数（无限不循环小数），并且Sn=a0.a1a2…an，那么，即：任意无理数都是一个有理数列的极限。

大学数学分析教材，在介绍了实数理论的相关理论之后，给出了确界的概念与确界存在唯一性定理。

定义1［8］（上确界） 设S是R中的一个数集，η是一个实数，若满足

①对任意x∈S，有x≤η，即η是S的上界；

②对任意a＜η，存在x0∈S，使得x0＞a，则称数η是数集S的上确界，记为η=supS。

定义2［9］（下确界） 设S是R中的一个数集，若ξ是一个实数，满足

①对任意x∈S，有x≥ξ，即ξ是S的下界；

②对任意β＞ξ，存在x0∈S，使得x0＜β，则称数ξ是数集S的下确界，记为ξ=infS。

从定义1与定义2可知，S上确界η=supS是S的最小上界，S下确界ξ=infS是S的最大下界。

定理［10］（确界唯一性） 设S⊂R是非空数集.若S有上界，则S必有上确界；若S有下界，则S必有下确界。

有了以上实数的极限理论基础，就可以建立以下实数域内指数函数的精确定义：

定义3［11］给定实数a＞0，a≠1设x为无理数，我们规定

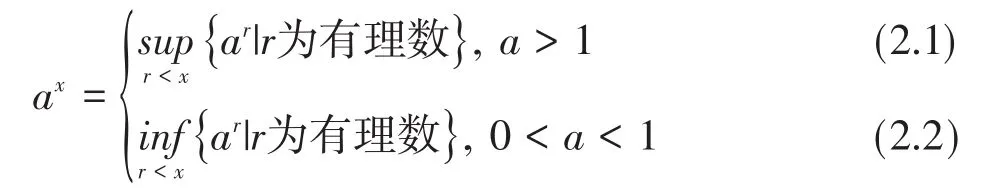
对任一无理数x，必有有理数r0，使x＜r0，则当有理数r＜x时，有r＜r0。由有理数乘幂的性质知：当a＞1时，有ar＜ar0。这表明非空数集{ar|r＜x,r为有理数} 有一个上界ar0。根据确界原理，该数集有上确界，所以(2.1)式右边是一个确定的定数。同理，当0＜a＜1时，(2.2)式右边也是一个定数。

如果把(2.1)、(2.2)两式中的“r＜x”改为“r≤x”，那么，无论r是无理数或是有理数，ax都可以用上述确界形式来统一表示。

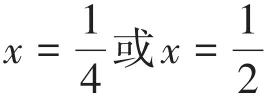
综上所述，规定：当a＞0且a≠1时，指数函数y=ax定义域为R。这样，指数函数的概念在实数范围内才得以完善。实数域内指数函数的性质也可以由极限运算法则得到，这里不再赘述。

3 指数函数在复数域内的延拓

现行的人教版高中数学教材［13］给出了复数概念与几何意义，并初步讨论了复数代数形式的四则运算，首先利用直角坐标与极坐标的关系，将非零复数z=x+iy表示为三角形式：

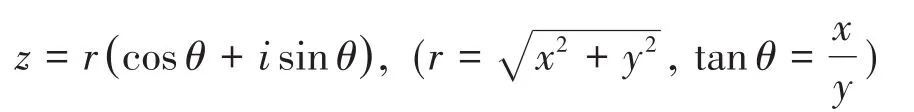
这里当r=1时，z=cosθ+isinθ，按照教材的阐述，如果利用欧拉公式

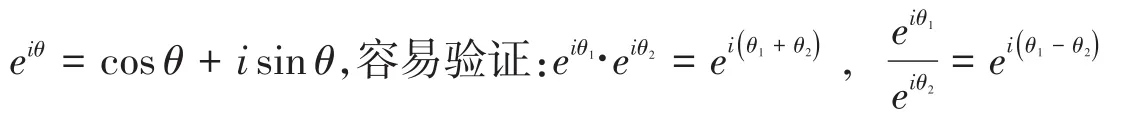
这样就得到了复数的指数形式：z=reiθ。教材存在的逻辑问题是：欧拉公式从何而来？

大学数学专业的课程体系中，通过数学分析与复变函数课程所建立的级数理论，为在复数域内推广指数函数奠定了基础。1715年英格兰数学家B.Taylor（1685-1731）提出了函数的幂级数表示公式［14］，其中指数函数ex(x∈R)的函数值可以由下面的幂级数得到，即：

由（3.1）来定义

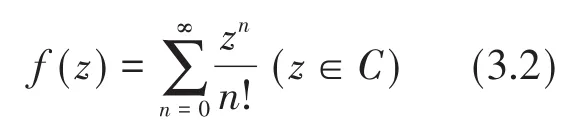
显然f(1)=e，由幂级数的性质和运算法则可以证明f(z)是连续的，并且f(z1+z2)=f(z1)f(z2)，当z=x∈R时，f(z)=ex，所以记f(z)=ez，因此，指数函数就在复数域内得到了推广，即

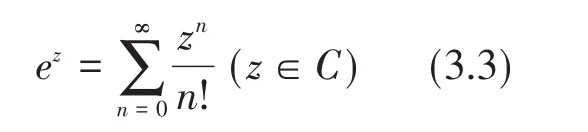
利用（3.3）可以证明著名的欧拉公式：eiθ=cosθ+isinθ。这样，中学教材中的复数指数表示才得以逻辑完整。

对于复指数函数ez，具有如下的性质：

（1）对于实数z=x（y=0）来说，定义与实指数函数的定义是一致的。

（2）ez|=ez＞0，argee=y；在z平面上ez≠0。

（4）对任意整数k，有ez·e2kπi=ez，因f(z+2kπi)=f(z)，所以ez是以2πi为基本周期的周期函数。

以上只是给出了复数域内一个常用的指数函数ez的定义，大学复变函数［15］给出了一般指数函数定义ω=az=ezlna(a≠0,∞,a∈C)。它是无穷多个独立的单值解析函数，详情这里不再赘述。

4 结论

深入分析中学数学教材的知识体系，对教材逻辑缺失部分进行补充与完善，为师范生构建一个较为严密的数学认知逻辑结构，对提高中学数学教师专业素养，培养合格的中学数学教师具有深远意义。数学师范生正处在数学知识体系构建与完善过程中，在数学学科相关课程学习完成后，有必要对初等数学知识进行再建与重构，这对指导中学数学教学有深远意义。