Chern-Simons Landau-Lifshitz模型自对偶方程静态解的存在性
陈智慧, 金广辉
(延边大学 理学院, 吉林 延吉 133002)
0 引言
本文考虑如下Chern-Simons Landau-Lifshitz模型的自对偶方程静态解的存在性问题:
D0φ=φ×D1D1φ-N2φ3(n×φ)-V′(τ-n·φ)(n×φ),
(1)
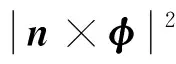
(2)
∂0N=-〈n×φ,D1φ〉,
(3)
∂1N=τ-φ3.
(4)
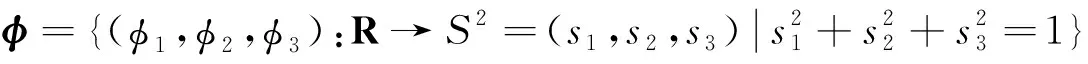
D1φ+Nφ×(n×φ)=0,
(5)
∂1N=τ-φ3.
(6)
Landau-Lifshitz方程是一类重要的非线性偏微分方程,由于其可描述磁性物质动态磁化现象,因此在铁磁物质的动态磁化理论研究和应用中具有重要作用[1-5].Chern-Simons Landau-Lifshitz方程(CSLL方程)在凝聚态物理、材料功能的应用等方面具有重要应用价值,但由于CSLL方程存在Chern-Simons规范场的耦合,因此对其研究存在较多困难.近年来,一些学者在适当假设的前提下对该方程的行波解、爆破解及解的渐进行为等问题进行了研究[6-10].本文基于上述研究,研究了CSLL方程自对偶情况下的静态解,并通过计算证明了CSLL方程具有能量守恒和规范不变的性质.
1 主要结果及其证明
定理1假设A1= 0, 则自对偶方程(5)和方程(6)有显式静态解:
其中C、C1和C2都是常数,且满足关系C1=kC2.
证明首先假设自对偶方程(5)的静态解的形式为:
φ(t,x)=(φ1(x),φ2(x),φ3(x)),N(t,x)=N(x).
(7)
则当A1= 0时,由式(3)有0=〈n×φ,D1φ〉=〈n×φ, ∂1φ+A1(n×φ)〉=〈n×φ, ∂1φ〉.将方程(5)两端与向量n×φ做内积可得:
0=〈n×φ, ∂1φ〉+A1〈n×φ,n×φ〉+N〈n×φ,φ×(n×φ)〉=
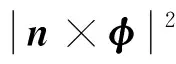
由上式可知假设A1= 0是合理的.将A1= 0代入方程(5)可得:
D1φ+Nφ×(n×φ)= ∂1φ+N(n-φ〈n,φ〉)= ∂1φ+N(n-φ3φ).
根据上式可将方程(5)和方程(6)化简为如下形式:
φ′1-Nφ1φ3=0,
(8)
φ′2-Nφ2φ3=0,
(9)
(10)
N′=τ-φ3.
(11)
显然,求解上述方程组的关键是求解φ3(x).假设:
(12)
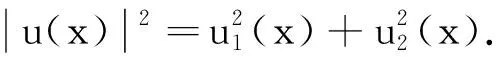
(13)
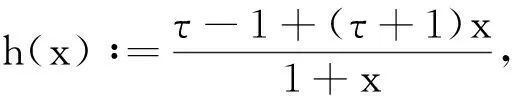
(ln (1+ρ)2+(τ-1)lnρ)′.
将上式左右两端同时积分并整理后可得:
(14)
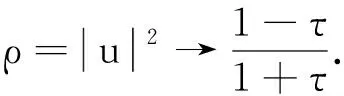
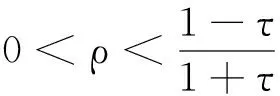
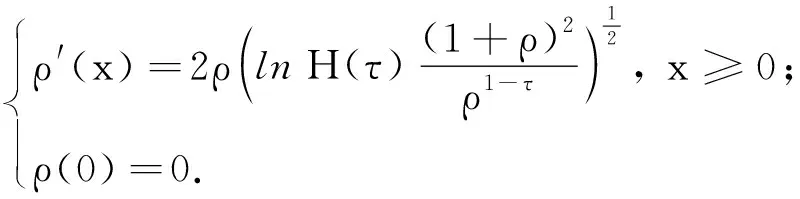
(15)
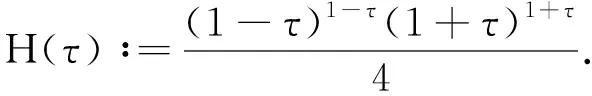
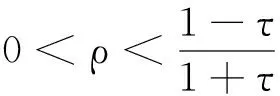
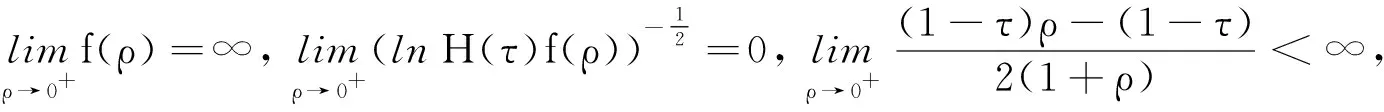
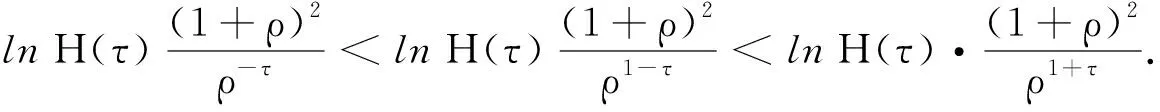
同理可得:
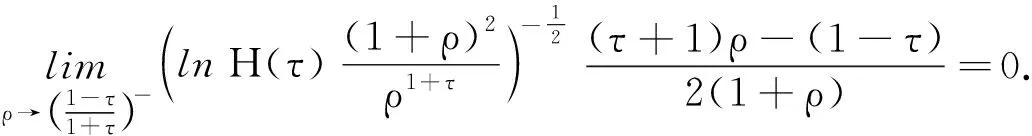
由于导数表示变化率,因此结合上述两个极限可知:
(16)
再由方程(8)和方程(9)可知φ1和φ2满足φ1=kφ2, 因此C1=kC2.定理1得证.
定理2若A0=φ3-τ, 则方程(5)和方程(6)的静态解φ=(φ1(x),φ2(x),φ3(x)),N=N(x)是系统(1)—(4)的解.
证明根据方程(5)可知D1φ=-Nφ×(n×φ)=-Nn+Nφ3φ, 由此得n×D1φ=n×(-Nn+Nφ3φ)=Nφ3(n×φ).又因为Dα(φ×ψ)=(Dαφ×ψ)+(φ×Dαψ), 所以有:
φ×D1D1φ=D1(φ×D1φ)=D1(φ×(-Nn+Nφ3φ))=D1(N(n×φ)).

2 性质
性质1系统(1)— (4)有如下守恒能量:
(17)
证明首先将方程(1)与φ做外积,然后再与D0φ做内积,则方程(1)可化简为
0=〈φ×(φ×D1D1φ),D0φ〉-N2φ3〈φ×(n×φ),D0φ〉-
V′(τ-n·φ)〈φ×(n×φ),D0φ〉=〈φ,D0φ〉〈φ,D1D1φ〉-〈D1D1φ,D0φ〉-
根据共轭导数的定义可得〈n,D0φ〉=〈n, ∂0φ〉+A0〈n,n×φ〉= ∂0φ3, 〈φ,D0φ〉=0, 因此上式可化简为0=-〈D1D1φ,D0φ〉-N2φ3∂0φ3-V′(τ-φ3)∂0φ3.利用公式DαDβφ=DβDαφ+Fα β(n×φ)及∂α〈φ,ψ〉=〈Dαφ,ψ〉+〈φ,Dαψ〉对上式进行计算可得:
将上式两端同时在R上积分可得:
因此系统(1)—(4)有如式(17)的守恒能量.
性质2系统(1)—(4)在如下规范变化下保持不变:
(18)
其中z=φ1+iφ2, 函数χ∈C∞(R1 + 1).
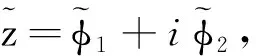
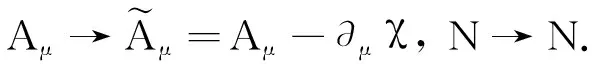
再根据共变导数的定义可知:
D0φ= ∂0φ+A0(n×φ)= ∂0(z,φ3)+A0(iz, 0)=(∂0z+iA0z, ∂0φ3).
类似上述方法可得:
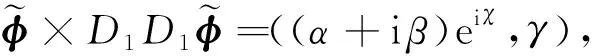
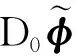
D1D1φ= ∂1(D1φ)+A1(n×D1φ)= ∂1(∂1z+iA1z, ∂1φ3)+A1(-A1z+i ∂1z, 0)=
(a,b,c).
由上式可得:
φ×D1D1φ=(cφ2-bφ3,aφ3-cφ1,bφ1-aφ2)=((cφ2-bφ3)+i(aφ3-cφ1),bφ1-aφ2).
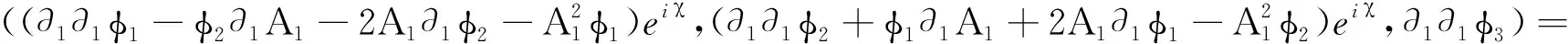

φ3(asinχ+bcosχ)+iφ3(acosχ-bsinχ)-i(φ1cosχ-φ2sinχ)c=
-icφ1(cosχ+i sinχ)+cφ2(cosχ+i sinχ)+iaφ3(cosχ+i sinχ)-bφ3(cosχ+i sinχ)=
(cφ2-bφ3)(cosχ+i sinχ)+i(aφ3-cφ1)(cosχ+i sinχ)=
(cφ2-bφ3)ei χ+i(aφ3-cφ1)ei χ,
(acosχ-bsinχ)(φ1sinχ+φ2cosχ)=bφ1-aφ2.
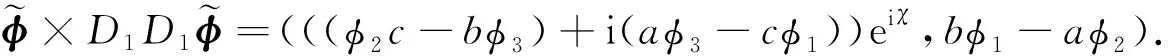
再根据Fμν的定义可知F01= ∂0A1-∂1A0.于是由函数χ∈C∞(R1 + 1)知F01经过变换后有
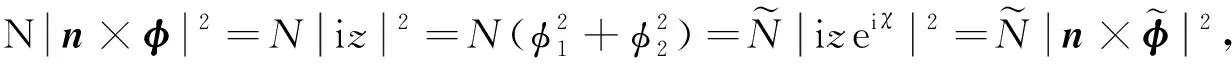
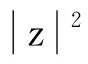
对上式进行变换后可得:
由上式可知方程(3)满足规范不变性.由上述显然知方程(4)也满足规范不变性,证毕.

