厘清指数函数与幂函数离切交的位置关系
广东省佛山市高明区第一中学(528500) 王顺耿
引例已知函数f(x)=在其定义域(0,+∞)内既有极大值又有极小值,则实数a的取值范围是( )
A.(0,1)∪(1,) B.(0,1) C.(,+∞) D.(1,)
因为f′(x)=x2−ax,要使函数f(x)在定义域(0,+∞)内既有极大值又有极小值,则导函数f′(x)有两个变号零点,即函数y=x2与函数y=ax有两个交点,探本溯源就是考察幂函数y=x2与指数函数y=ax图象的位置关系.事实上,我们学习了指数函数和幂函数,但对它们间较为深入的函数图象位置关系还缺少研究,明确它们间的位置关系对某些问题的研究有一定的帮助,下面对两函数图象的位置关系做进一步的探究.
1 指幂两函数图象的位置分析
指数函数y=ax(a >0,a≠1)图象分布在第一、二象限,幂函数y=xα(α≠0)图象主要分布在第一象限,当幂函数又是偶函数时,第二象限图象与第一象限图象对称,下面依据底数a和幂指数α的变化,从三个角度对两函数图象的位置关系作深入探究.
1.1 确定的幂函数与变化的指数函数
幂函数y=xα(α≠0)的幂指数α确定,探究随着指数函数y=ax(a >0,a≠1)底数a的变化,两函数图象的位置关系,先考察两函数在(0,+∞)上的位置关系.

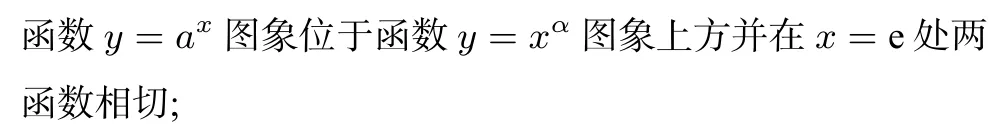
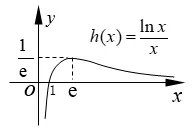
③若0 ④若lna <0,则0< a <1,函数y=lna与函数f(x)=相交一点,方程ax=xα一解,在(0,+∞)上,函数y=ax图象与函数y=xα图象在x=x0(x0∈(0,1))处相交. ⑧若lna >0,则a >1,函数y=lna与函数f(x)=相交一点,方程ax=xα一解,在(0,+∞)上,函数y=ax图象与函数y=xα图象在x=x0(x0∈(0,1))处相交. 特别地,当幂函数y=xα又是偶函数时,在(−∞,0)上,指数函数y=ax图象与幂函数y=xα图象的位置关系探究如下: 由a−x=(−x)α=xα(x >0,x≠1),得=−lna,同样令f(x)=. (1)当α>0 时,据图1 有以下结论: 图1 ①当−lna >,即0< a <(<1)时,a−x >(−x)α,在(−∞,0)上,函数y=ax图象在函数y=xα图象上方; ②当−lna=,即a=(<1)时,在(−∞,0)上,函数y=ax图象位于函数y=xα图象上方并在x=−e 处两函数相切; ③当0<−lna <,即< a <1 时,在(−∞,0)上,函数y=ax图象与函数y=xα图象在和处相交; ④当−lna <0,即a >1 时,在(−∞,0)上,函数y=ax图象与函数y=xα图象在x=∈(−1,0))处相交. (2)当α<0 时,据图2 有以下结论: 图2 ⑤当−lna <,即a >(>1)时,a−x <(−x)α,在(−∞,0)上,函数y=ax图象在函数y=xα图象下方; ⑥当−lna=,即a=(>1)时,在(−∞,0)上,函数y=ax图象位于函数y=xα图象下方并在x=−e 处两函数相切; ⑧当−lna>0,即0 指数函数y=ax(a >0,a≠1)的底数a确定,探究幂函数y=xα(α≠0)随着幂指数α的变化,两函数间的位置关系,先考察两函数在(0,+∞)上的位置关系. (1)当a >1 时,lna >0,x=e 是函数g(x)在(1,+∞)上的极小值点,也是(1,+∞)上的最小值点,g(x)min=g(e)=e lna >0,如图3 所示,依图3 有下面结论: 图3 ①若α <0,函数y=α与函数g(x)=相交一点,方程ax=xα一解,在(0,+∞)上,函数y=ax图象与函数y=xα图象在x=x0(x0∈(0,1))处相交; ②若0< α ③若α=e lna,函数y=α与函数g(x)=相切,在(0,+∞)上,函数y=ax图象位于函数y=xα图象上方并在x=e 处相切; ④若α >e lna,函数y=α与函数g(x)=相交两点,在(0,+∞)上,函数y=ax图象与函数y=xα图象在x=x1(x1∈(1,e))和x=x2(x2∈(e,+∞))处相交. (2)当0< a <1 时,lna <0,x=e 是函数g(x)在(1,+∞)上的极大值点,也是(1,+∞)上最大值点,g(x)max=g(e)=e lna <0,如图4 所示,依图4 有下面结论: 图4 ⑤若α >0,函数y=α与函数g(x)=相交一点,在(0,+∞)上,函数y=ax图象与函数y=xα图象在x=x0(x0∈(0,1))处相交; ⑥若e lna < α <0,有< α(x >1)和> α(0< x <1),即ax < xα(x >0),在(0,+∞)上,函数y=ax图象在函数y=xα图象下方; ⑦若α=e lna,函数y=α与函数g(x)=相切,在(0,+∞)上,函数y=ax图象位于函数y=xα图象下方并在x=e 处相切; ⑧若α 同样地,给定指数函数y=ax,当幂函数y=xα又是偶函数时,在(−∞,0)上,幂函数y=xα图象与指数函数y=ax图象的位置关系,探究如下: 由a−x=(−x)α=xα(x >0,x≠1),得=−α,同样令g(x)=. (1)当a>1 时,据图3 有以下结论: ①当−α<0,即α>0 时,在(−∞,0)上,函数y=xα图象与函数y=ax图象在处相交; ②当0<−α ③当−α=e lna,即α=−e lna时,在(−∞,0)上,幂函数y=xα又是偶函数时,其函数图象位于指数函数y=ax图象上方并在x=−e 处相切; ④当−α >e lna,即α <−e lna时,在(−∞,0)上,函数y=xα图象与函数y=ax图象在x=∈(−∞,−e))和处相交. (2)当0 ⑤当−α>0,即α<0 时,在(−∞,0)上,幂函数y=xα图象与指数函数y=ax图象在处相交; ⑥当e lna <−α <0,即0< α <−e lna时,有<−α(x >1)和>−α(0< x <1),即a−x > xα=(−x)α(x >0),在(−∞,0)上,幂函数y=xα图象在指数函数y=ax图象下方; ⑦当−α=e lna,即α=−e lna时,在(−∞,0)上,幂函数y=xα又是偶函数时,其函数图象位于指数函数y=ax图象下方并在x=−e 处相切; ⑧当−α 当幂指数α=底数a时,探究指数函数y=ax(a >0,a≠1)与幂函数y=xa(a >0,a≠1)的位置关系,先考察在(0,+∞)上的位置关系. 由ax=xa,得,令h(x)=,由h′(x)==0,得x=e 是函数h(x)在(0,+∞)上的极大值点,也是最大值点,h(x)max=h(e)=,如图5 示,依图5 有下面结论: 图5 ④若−<0,则>0,由图5 可得a >1,在(−∞,0)上,幂函数y=xα图象与指数函数y=ax图象在x=∈(−1,0))处相交. 这样,就将指数函数与幂函数离切交的位置关系进行了完整地探究,综合上述探究,还可以得出一个一般性的结论: 若指数函数y=ax(a>0,a≠1)与幂函数y=xα(α≠0)在(0,+∞)上相切,必在x=e 处相切;在(−∞,0)上相切,必在x=−e 处相切. 例1 见文首“引例”. 解由1.1 中的③得,当1< a <时,函数y=ax图象与函数y=xα图象在x=x1(x1∈ (1,e))和x=x2(x2∈(e,+∞))处交叉相交,故选D. 例2 已知不等式在(0,+∞)上恒成立,则t的取值范围是____. 解由1.2 中的⑥、⑦得,当e ln≤t+1<0,即−(1+e ln 3)≤t<−1 时,上述不等式在(0,+∞)上恒成立. 依据1.3 中的函数h(x)=及图5 可得结论: 题4 (2015年高考山东文科第3题)设a=0.60.6,b=0.61.5,c=1.50.6,则a,b,c的大小关系是( ) A.a C.b 解据上面结论,显然为b 例5 比较与与πe的大小 解据上面结论,显然有 仔细体会上述的探究方法及其结论,当我们碰到需要考虑指数函数与幂函数位置关系的问题时,就可以汲取上述的研究方法或结论,以便快速方便地去解决相关指幂函数间的问题.
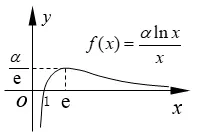
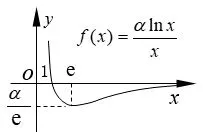
1.2 确定的指数函数与变化的幂函数

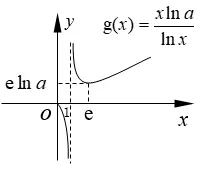

1.3 底数a 与幂指数α 同步变化


2 简单应用


