考虑冗余系统时变故障率和更新过程的MMC可靠性建模及其应用

吴科成，王凤学，吴晗，曲毅，董红，欧阳森

(1.广东电网有限责任公司，广州市 510600；2.华南理工大学电力学院，广州市 510640；3.广东电网有限责任公司电网规划研究中心，广州市 510030；4.广东电网广州供电局，广州市 510610)

0 引 言

柔性直流输配电系统中的关键设施大量使用模块化多电平换流器(modular multi-level converter，MMC)，例如变流器、直流变压器、直流断路器等。而冗余设计是当前MMC的一种重要模式，MMC中的冗余系统会影响到其可靠性[1-2]，其中的时变故障率和更新过程目前尚有诸多量化工作需要进一步讨论。

现阶段非冗余系统下，设备可靠性通常采用马尔科夫过程[3-4]和蒙特卡洛法[5]进行评估，虽然MMC中并非都有冗余系统，但冗余系统是配电网中MMC的主要模式，而冗余元件的配置将会导致传统马尔科夫过程理论分析的复杂化和蒙特卡洛计算量的急剧增大。针对MMC冗余系统的研究中，为减少计算量，大多采用传统马尔科夫过程进行细致建模。文献[6-8]基于马尔科夫过程，以k/n(G)工作冗余系统的MMC为例进行可靠性建模；文献[9]将冗余系统分为被动备用策略和主动备用策略，分别推导2种策略下k/n(G)系统的可靠度。但上述文献由于未考虑冗余设计会导致MMC整体故障率时变的问题，因此所求得的冗余系统下MMC可靠性结果可能过于乐观。

在考虑故障率时变和设备更新的研究中，以半马尔科夫和蒙特卡洛法为主。文献[10]侧重于分析MMC子模块老化等因素导致故障率时变，采用半马尔科夫过程建立含修复过程的MMC多状态数学模型，但半马尔科夫的计算难度和复杂度会随冗余器件的增加而急剧增大，实际应用较为困难。文献[11-12]采用非序贯蒙特卡洛法获取MMC内部元件的寿命分布，同样侧重于分析老化等因素的影响，但蒙特卡洛法计算量较大，且其结果的准确性受限于样本选取。

可见，目前的研究工作已开始将冗余系统纳入MMC的可靠性计算过程，但没有进一步考虑到冗余系统更新过程的量化分析，以及对MMC可靠性的影响，主要存在以下不足之处：1)未对MMC冗余系统进行科学分类，大多仅对单一的k/n(G)冗余系统进行建模；2)当MMC内部元件可靠度服从指数分布时，并不能科学表征具有多个冗余系统结构的MMC的时变性故障率；3)未能将MMC在经历更新或修复过程纳入可靠性的量化表征中。

针对上述问题，本文提出一种考虑冗余系统时变故障率和更新过程的MMC可靠性建模方法。首先从冗余方式、冗余程度2个维度归纳4种主要冗余系统可靠性模型，从定义的角度出发分析现有方法求解故障率公式存在的问题，即未考虑故障率时变性导致求解参数过低而可靠性计算结果偏高的问题。然后，在以N阶梯故障率代替时变故障率的基础上，引入更新过程理论，求解MMC的平均无故障工作时间(mean time to failure,MTTF)和稳态可用度。最终建立考虑冗余系统时变故障率和更新过程的MMC可靠性评估模型，以解决传统方法未充分考虑冗余系统故障率时变、传统冗余系统未考虑更新过程问题。

此外，为简化叙述，1)本文设定MMC内部元件故障率恒定、可靠度服从指数分布，非指数分布的情况同理可得；2)本文所讨论的是具有冗余系统结构的MMC。

1 冗余系统可靠性建模

1.1 冗余系统可靠度

通过对一个元件添加并联元件，从而达到提高系统可靠性的目的，这种方法在设计中称为冗余。根据冗余方式可将冗余系统分为工作冗余系统和储备冗余系统，而根据冗余程度可将冗余系统分为并联系统和k/n(G)系统[13-21]。根据MMC可靠性的计算需求，首先对4种冗余系统的可靠度进行分析。

工作冗余与储备冗余的区别在于冗余元件是否参与工作，前者参与，后者处于备用状态；并联冗余和k/n(G)系统的区别在于工作所需元件数量的不同，前者仅需一个元件即可工作，后者n个元件中至少需要k个(k≤n)元件才可工作。冗余方式、冗余程度2个维度间相互匹配则可得到4种主要的冗余系统，即并联工作冗余系统、并联储备冗余系统、k/n(G)工作冗余系统和k/n(G)储备冗余系统，如图1所示。

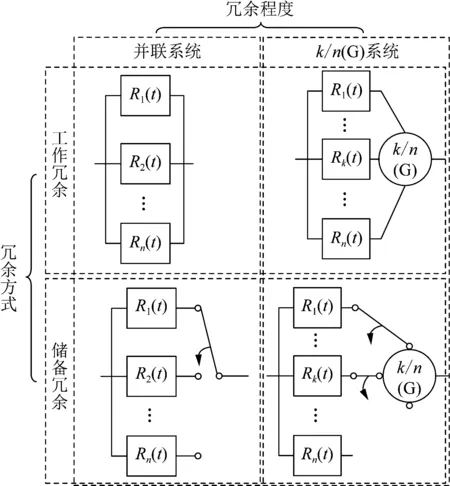
图1 冗余系统分类Fig.1 Classification of redundant systems

(1)

式中：Rr(t)为冗余系统中各元件的可靠度函数。现有可靠性研究大多做出以下假设：冗余系统中各元件可靠度函数均服从指数分布，且尺度参数均相同[22-26]。

设备可靠性参数主要与其可靠度函数、故障率有关，例如平均无故障时间、可用度等。因此本文所研究的可靠性建模是在设备内部元件可靠度函数服从指数分布、尺度参数均相同的基础上，通过式(1)对MMC冗余系统整体可靠度及其故障率进行分析。

1.2 冗余系统故障率

本文所讨论冗余系统可靠性建模的前提为各元件的可靠度函数均服从故障率λ恒定的指数分布，即具有无记忆性的特点，这也是当前诸多可靠性研究的基础。此时系统内部元件的可靠度函数为R(t)=e-λt，而其冗余系统的可靠度函数可根据式(1)进行计算，则时变特性问题的关键在于冗余系统的故障率求解及其处理。

1.2.1 非冗余系统故障率

对于非冗余系统即串联系统，其系统可靠度函数RS(t)为：

RS(t)=R1(t)×R2(t)×…×Rn(t)=
e-λ1t×e-λ2t×…×e-λnt=
e-(λ1+λ2+…+λn)t=e-λSt

(2)

式中：λ1，λ2，…，λn分别为组成非冗余系统的n个元件的故障率；λS为非冗余系统故障率。

根据式(2)可知，非冗余系统的可靠度函数仍为指数函数，其平均无故障时间TMTTF为：

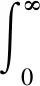
(3)

根据式(2)、(3)可得非冗余系统故障率λS为：

λS=1/TMTTF

(4)

可见，非冗余系统故障率是平均无故障时间的倒数，这是由于其设备可靠度函数仍旧为指数分布，导致积分结果为常数，因此设备可靠度函数是否为指数分布是使用式(4)求解其等效故障率的依据。

1.2.2 冗余系统时变故障率分析

对于冗余系统，各元件可靠度函数代入式(1)后，其可靠度函数将不再为故障率恒定的指数分布，因此MMC冗余系统等效故障率的求解将不能以式(4)为参考进行，而是应从故障率的定义进行求解。故障率定义公式可表示为[27]：

λ(t)=-dR(t)/[R(t)dt]

(5)

式中：λ(t)为MMC冗余系统故障率参数。

现有传统方法[6-9]对此的研究是在求解冗余系统的故障率时，直接通过式(3)、(4)求解TMTTF，进而得到恒定的系统故障率参数，并未考虑MMC冗余系统可靠度不服从指数分布的问题。

现以k/n(G)工作冗余系统为例，假设k=6，n=9，各内部元件的故障率均为λr=0.1次/a，冗余系统故障率求解结果如图2所示。其余类型的冗余系统故障率对比见附图A1。

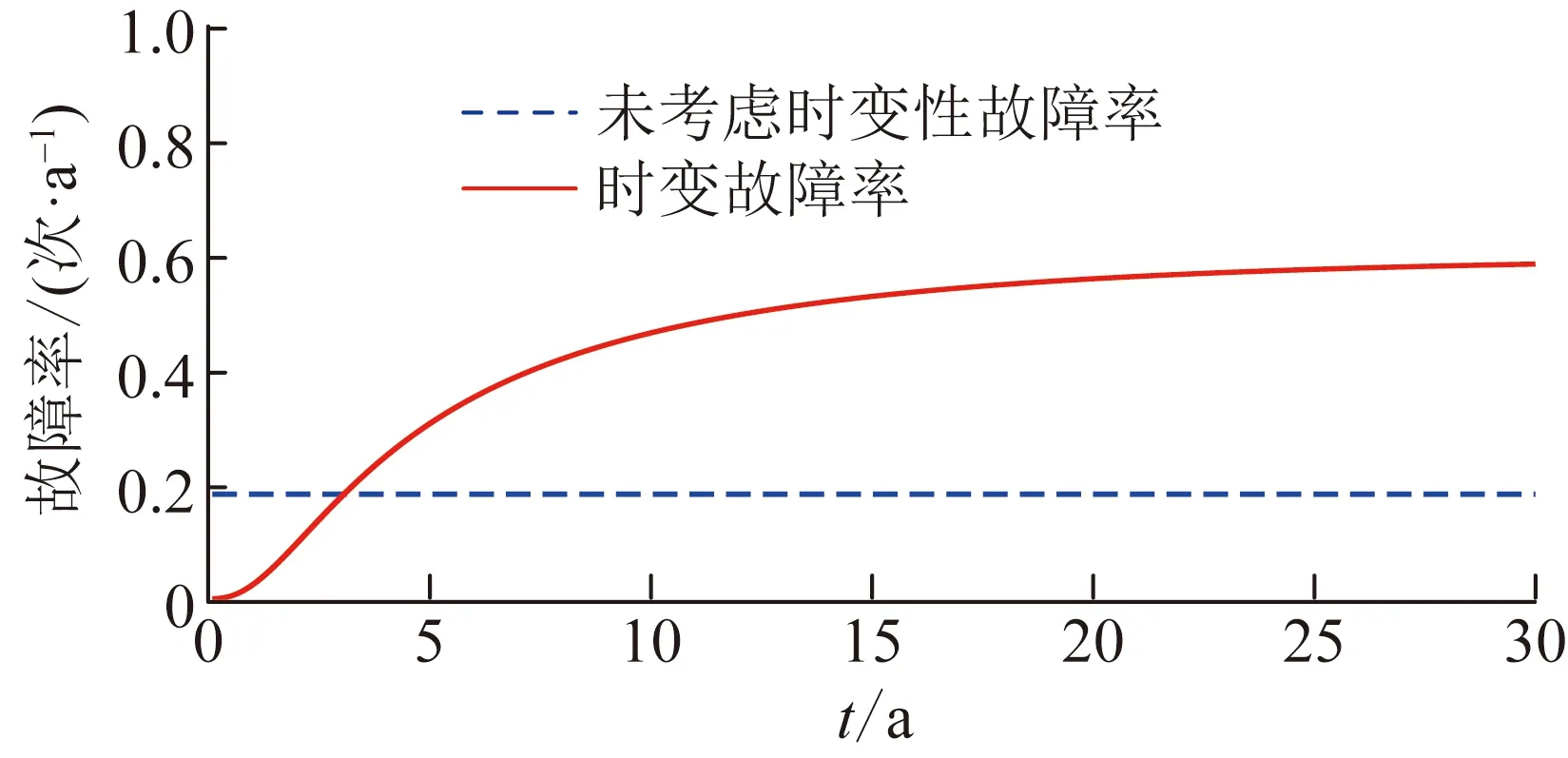
图2 是否考虑故障率时变对比Fig.2 Time-varying comparison considering failure rate or not

图2中，实线为根据式(5)定义求解得出的时变故障率；虚线为根据式(4)所求的未考虑时变性的故障率。由图2可知，若不考虑冗余系统的故障率时变性，传统方法[6-9]得到的系统故障率参数λ虚线，整体数值偏低，即当t→∞时，λ虚线=0.183次/a <λ实线≈0.589次/a。

1.2.3 冗余系统时变故障率的均值求解

分析图2曲线可知，冗余系统时变故障率曲线单调递增，但其增长速度随时间趋于0，这是由于在设定内部元件故障率恒定的条件下，根据式(1)所得的MMC冗余系统可靠度为指数分布的线性组合，因此由式(5)所得时变故障率表达式为分式，分子分母同样为指数分布的线性组合，当t→∞时，时变故障率趋于一个常数。

故此，若要求解时变故障率的均值，可在设定等效年限L的基础上，通过式(6)求解：

(6)

式中：λimp为时变故障率的均值，实际为0～L时间段内设备时变故障率的均值；L为等效年限。

根据图2以及前文分析，随着等效年限L的增大，MMC冗余系统的时变故障率逐渐趋于一个常数，时变故障率均值增量Δλimp趋于0。因此，等效年限L可根据时变故障率均值增量Δλimp进行确定：

1)设定时变故障率均值增量占比Δλimp的阈值λT，本文设为λT=0.01。

2)基于式(5)所得MMC冗余系统时变故障率，通过式(7)求解等效年限L数值，为方便后续计算，将L向上取为整数。

(7)

3)时变故障率均值增量Δλimp随等效年限L的变化曲线如图3所示，随着等效年限L的增加，Δλimp先升高后降低。这是由于前期故障率均值位于0附近，其增量较小，而随着L的增加，λimp和Δλimp均增大；当达到一定年限后，时变故障率λimp曲线趋于平缓，Δλimp不断减小，因此λT与Δλimp有两处交点。一般讨论中都会选择数值较大的交点作为L数值。

图3 时变故障率均值增量占比变化Fig.3 Proportion change of the mean increment of time-varying failure rate

此时，等效年限L=18 a，时变故障率均值λimp≈0.551次/a>λ虚线=0.183次/a，验证了未考虑冗余系统故障率时变性时，所求故障率较小。

等效年限L的设置不仅是为了求解时变故障率均值，更重要的是为后续采用N阶梯故障率代替时变故障率提供相应的理论依据。限于篇幅，上述分析皆基于可靠度函数为指数而展开，而非指数分布的情况也可进行类似分析获得时变故障率的量化计算公式。

2 考虑更新过程的MMC可靠性计算

基于1.2节所提冗余系统故障率的时变性问题，对冗余系统下的MMC可靠性模型建模遵循以下3个原则：1)随着时间的累积，故障率随之增大，即故障率具有“时变性”特点；2)需考虑更新过程对冗余系统时变故障率的影响，即每次更新器件后系统可恢复至“如新”状态，故障率从0时刻状态开始重新增长；3)更新过程发生的时刻具备随机性，但期间MMC的修复率μ恒定。

为体现冗余系统故障率时变性的特点，可采用分割时间断面的思路，使用N阶梯故障率代替时变故障率[22]，一方面，可通过不断分割时间断面逼近实际故障率曲线；另一方面，在分割的时间段内系统故障率恒定，可采用更新过程理论推导求解系统的寿命分布函数和更新周期函数，最终得到可靠性指标TMTTF和可用度。

本文可靠性建模与传统N阶梯故障率可靠性建模[22]的不同在于：一方面是研究问题的不同，传统N阶梯故障率可靠性建模未考虑冗余系统的影响，侧重于内部组件具备老化故障率的建模；本文侧重于讨论现有文献在假定MMC内部元件故障率恒定时，存在未充分考虑冗余系统故障率时变的问题。另一方面是取代对象的不同，传统N阶梯故障率可靠性建模以服从威布尔分布的老化故障率作为N阶梯故障率的取代对象，随着时间的增长其故障率近似成指数增大，本文主要研究的是配置冗余导致原本恒定故障率发生时变性的变化，时变故障率随时间的增长且其变化曲线趋于平缓，故障率之间较大的差异也会导致设备的可靠性建模有所区分。

2.1 N阶梯更新过程的MMC可靠性模型

为建立N阶梯更新过程的MMC可靠性模型，须首先选取N阶梯故障率对MMC时变故障率进行拟合，从而分时段对MMC寿命分布及更新周期公式进行推导，最终求解MMC的TMTTF参数及其稳态可用度。

2.1.1N阶梯故障率的选择

考虑到冗余系统故障率为导数递减的增函数，可通过选择适当的等效年限L，使得第N阶段趋近于实际故障率变化曲线，如图4所示，等效年限L的选取方法见1.2.3节。

图4 N阶梯故障率变化曲线Fig.4 The curve of N-step failure rate

根据图4可知，以1 a为区间长度取前N-1个阶段的故障率，遵循保守原则，各个阶段故障率数值取该区间内故障率的最大值，即第N个区间故障率取第N个年限的故障率数值，计算公式为：

(8)

式中：ti(i=1,2,… ,N)为第i年；λi(i=1,2,… ,N)为第i年的故障率。

2.1.2 MMC寿命分布函数及更新周期函数

N阶梯更新过程MMC停运模型如图5所示，图5(b)中阴影部分为MMC更新所需时间。

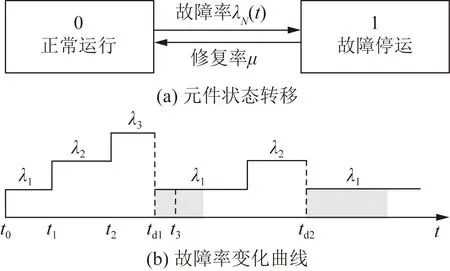
图5 N阶梯更新过程MMC停运模型Fig.5 The MMC outage model of N-step renewal process

根据图5(a)可知，将MMC整体作为元件进行更新修复，仅考虑故障停运，则其状态转移图属于两状态模型，当故障率λN(t)恒定时，即为文献[15-16]中的两状态马尔科夫模型。

根据图5(b)可知，MMC停运时刻td既可能出现在故障率为λ3时间段，也可能出现于故障率为λ2的时间段内，具备随机性，因此考虑更新过程后MMC冗余系统故障率无法用时域上的解析式表达。采用更新过程理论后可直接求解设备的寿命分布函数及更新周期函数[27]。

设Yi为MMC第i次投入运行后的寿命，Gi为MMC第i次更新修复的时长，则Zi=Yi+Gi为第i次更新周期，MMC的修复率恒定为μ，即修复时长分布服从G(t)=1-e-μt的指数分布。当采用N阶梯更新过程的MMC停运模型时，相应地，寿命分布函数和更新周期的求解也应分为N种情况进行讨论，具体推导过程详见附录A.1。

根据N种情况讨论结果，采用全概率公式，可得到N阶梯故障率下MMC的寿命分布函数F(t)：

(9)

N阶梯故障率下MMC的更新周期Zi的概率分布函数W(t)可通过卷积公式求解[22]：

(10)

式中：tk代指第k年，出现的t0特指开始时间，设为0。

2.2 MMC可靠性参数推导

以元件可靠度服从指数分布为前提，冗余系统可靠性参数选用TMTTF[6-8]。考虑更新过程后MMC可靠性参数还包括可用度[14-15]。

本文基于2.1节所求N阶梯故障率下MMC寿命分布函数和更新周期函数，通过TMTTF定义公式和可用度卷积公式，分别推导MMC的TMTTF参数以及其稳态可用度。

2.2.1TMTTF公式推导

TMTTF是可修复产品在相邻两次故障之间工作时间的数学期望值，其定义公式为：

(11)

式中：f(t)为MMC的寿命概率密度函数，为F(t)的导数；R(t)为设备的可靠度函数，与F(t)之和为1。

根据式(9)与式(11)，可求解得出N阶梯更新过程MMC停运模型的TMTTF指标：

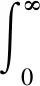
(12)

2.2.2 稳态可用度公式推导

可用度A(t)是指系统在t时刻开始功能正常的概率，与可靠度R(t)不同之处在于其不考虑t时刻之前是否发生故障，而仅考虑该时刻的正常运行概率。稳态可用度是取t→∞时的A(t)值。

依据更新过程理论[27]，可用度A(t)满足以下等式：

A(t)=1-F(t)+A(t)*w(t)

(13)

式中：w(t)为更新周期概率密度函数，为W(t)导数；*为卷积运算符。

根据式(9)、(10)和(13)，可求解N阶梯更新过程MMC停运模型的稳态可用度指标：

(14)

由式(14)可知，当各阶梯故障率λi(i=1,2,…,N)相等时，即认为MMC冗余系统故障率恒定，稳态可用度退化为A(t)=μ/(μ+λ1)，因此两状态马尔科夫模型为不考虑故障率时变情况的特例。

2.3 计算流程

考虑冗余系统更新过程的配电网MMC可靠性建模方法计算流程如图6所示，具体流程如下：

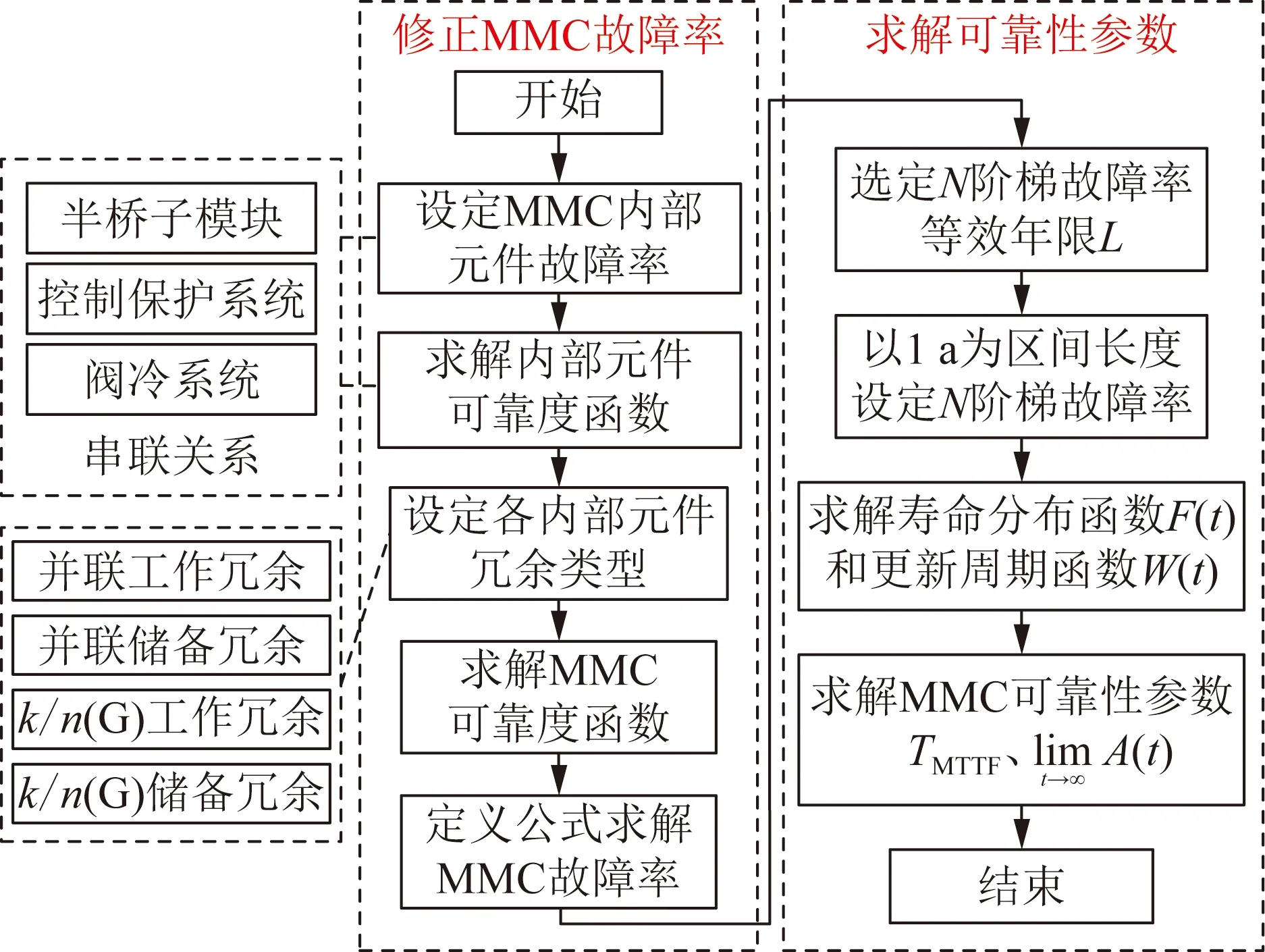
图6 计算流程Fig.6 The calculation flowchart

步骤1：输入MMC内部元件故障率参数，此处假定各内部元件故障率恒定，故障时间服从指数分布；

步骤2：根据故障率可分别求解内部元件可靠度函数；

步骤3：设定MMC内各元件的冗余类型；

步骤4：基于式(1)对冗余系统下的MMC进行可靠性建模，得到其可靠度函数；

步骤5：根据步骤4所得MMC可靠度函数，采用定义式(5)对MMC冗余系统故障率求解；

步骤6：依据2.1.1节选定N阶梯故障率等效年限L；

步骤7：基于式(9)、(10)求解MMC寿命分布函数F(t)、更新周期函数W(t)；

步骤8：基于式(12)、(14)求解MMC可靠性参数TMTTF和稳态可用度。

3 算例分析

3.1 MMC可靠性建模及参数设定

3.1.1 MMC可靠性建模

本文以基于半桥子模块的MMC为例进行建模分析，其拓扑结构如图7示。其包含3相6桥臂，且各桥臂由n个相同的半桥子模块共同构成的相单元和1个电抗器串联而成。半桥子模块可靠性主要由IGBT模块、电容、子模块控制器(包括驱动板、主控板、通信等，下同)、取能电源等共同决定。各桥臂单元中半桥子模块分别由阀基控制设备进行上层调控。另外，MMC的安全可靠性运行还与控制保护系统和阀冷系统密切相关。

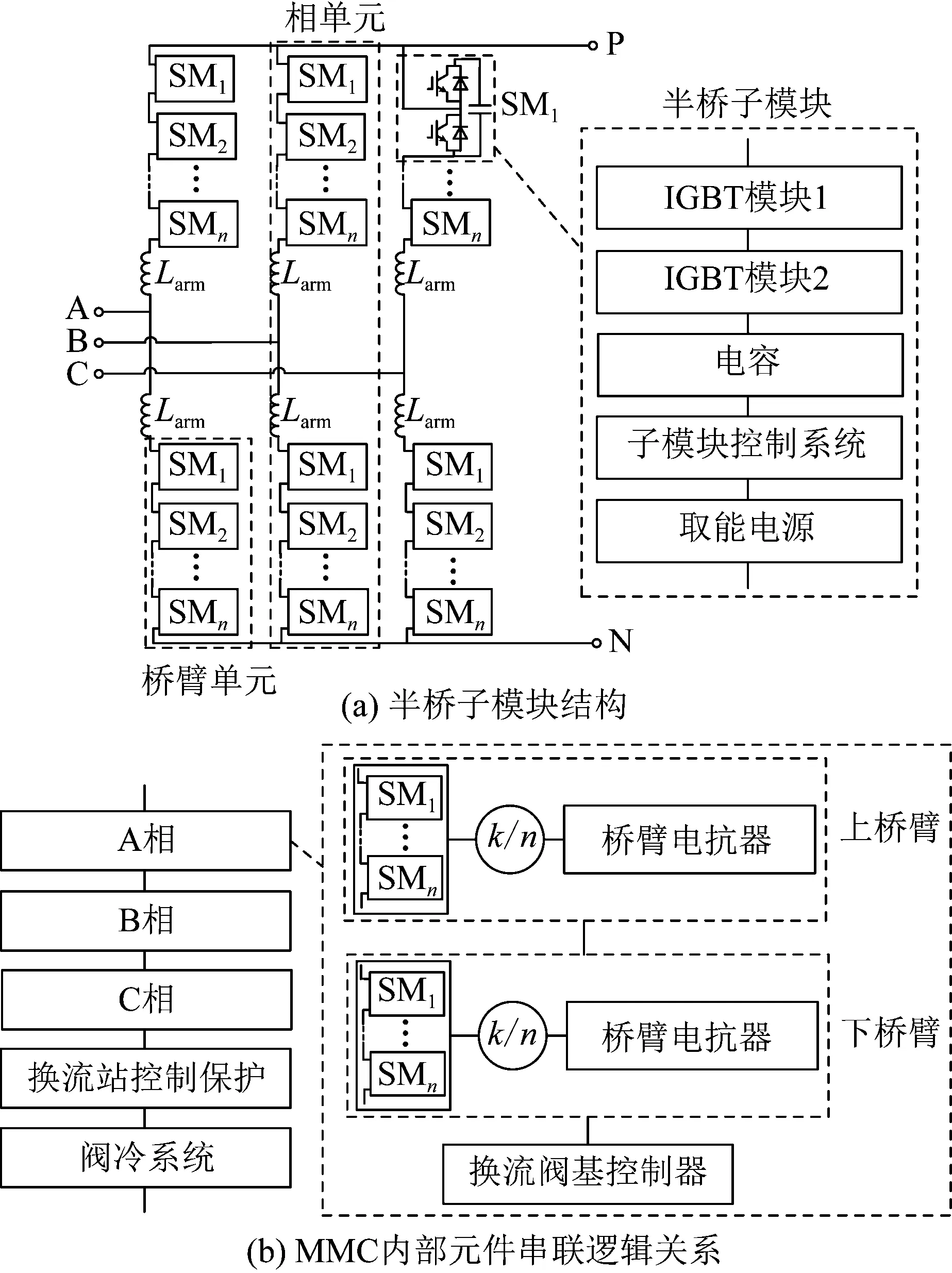
图7 基于半桥子模块的MMC拓扑结构Fig.7 MMC topology based on half-bridge sub-module

根据图7(b)中串联逻辑关系，基于半桥子模块的MMC可靠度函数RMMC(t)计算公式为：

RMMC(t)={[RBAU(t)]2RVBC(t)}3RCP(t)RVC(t)

(15)

式中：RBAU(t)、RVBC(t)、RCP(t)和RVC(t)分别为桥臂单元、阀基控制设备、控制保护系统以及阀冷系统的可靠度函数，其冗余配置分别对应图1中4种类型的冗余系统，具体建模详见附录A.2。

3.1.2 MMC参数设定

本文算例假设MMC将AC 10 kV换流为DC 10 kV，MMC修复率μ=0.402，其他内部元件可靠度函数服从指数分布，故障率均选自参考文献[9,24-26]，具体见表1。

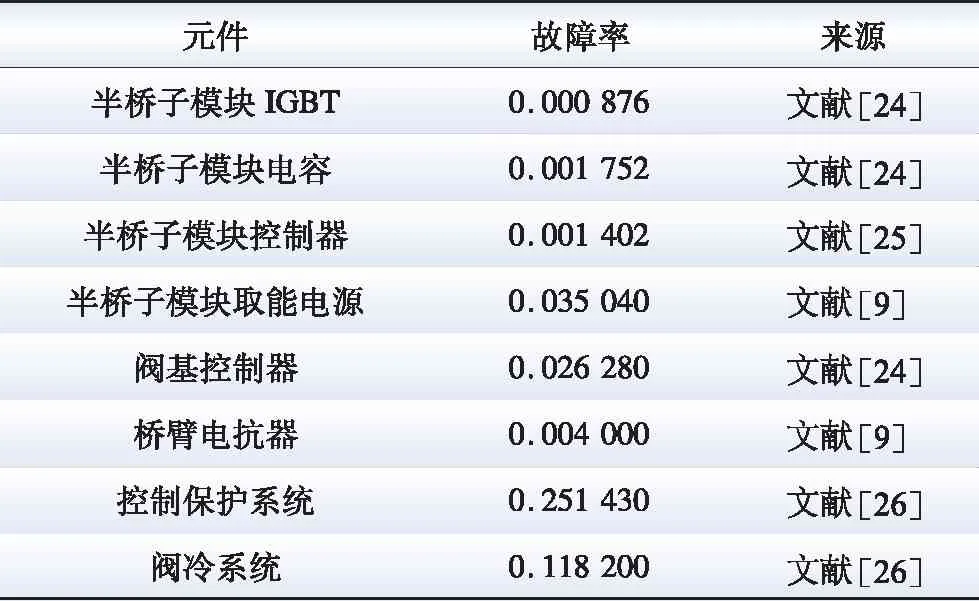
表1 MMC内部元件故障率Table 1 Failure rate of the internal components in MMC

根据故障率选择的不同，本文采用4种方法求解MMC可靠性参数并对比：

传统方法[6-9]：未考虑MMC冗余系统时变故障率；

蒙特卡洛法：对时变故障率进行模拟；

保守蒙特卡洛法：默认MMC冗余系统故障率为恒定值，其值为等效年限L处的故障率；

本文方法：采取N阶梯故障率代替MMC冗余系统时变故障率，建立其可靠性模型。

传统方法采用式(4)求解所得故障率λtr=0.332次/a；采用定义式(5)可得MMC冗余系统时变故障率，其等效年限L内的均值λimp=1.345次/a，等效年限L处故障率λL=1.792次/a；N阶梯故障率λN(t)可由式(8)所得，故障率对比如图8所示。

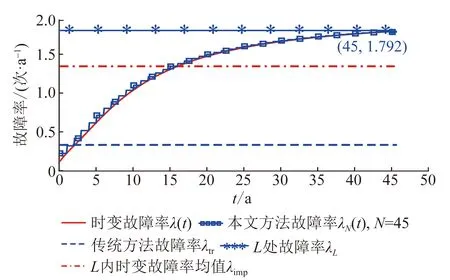
图8 MMC冗余系统故障率选择对比Fig.8 Comparison of the selection of the failure rates of MMC redundant system

3.2 仿真结果

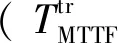
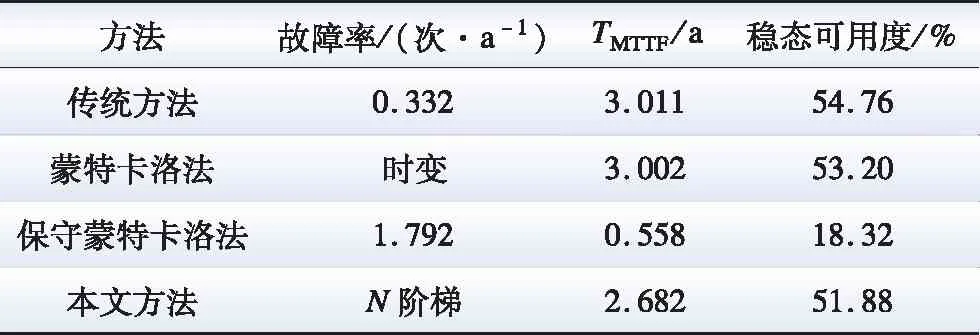
表2 可靠性参数对比Table 2 Comparison of reliability parameters

根据表2可知：

2)保守蒙特卡洛法可靠性参数远低于蒙特卡洛法，原因在于保守蒙特卡洛法故障率选自等效年限L处故障率，而MMC无故障运行L年的概率不足1%，直接采用λL会导致MMC冗余系统故障率过大，因此保守蒙特卡洛法所求可靠性参数过于保守。

4)本文所提方法所得可靠性参数大小处于蒙特卡洛和保守蒙特卡洛之间，这是由于时变故障率和N阶段故障率在等效年限L内的均值小于λL，所以本文方法的TMTTF和可用度均小于保守蒙特卡洛；同时N阶段故障率在等效年限L内整体大于时变故障率λ(t)，因此与蒙特卡洛法相比，本文方法在减少计算成本的同时，可得出相对保守的可靠性参数。

3.3 冗余度对可靠性参数的影响

为确定冗余度对本文所提考虑冗余系统时变故障率和更新过程的MMC可靠性模型的影响，通过改变MMC半桥子模块冗余度(即k、n比例)，观测本文方法所得TMTTF和稳态可用度的变化，结果如表3所示。

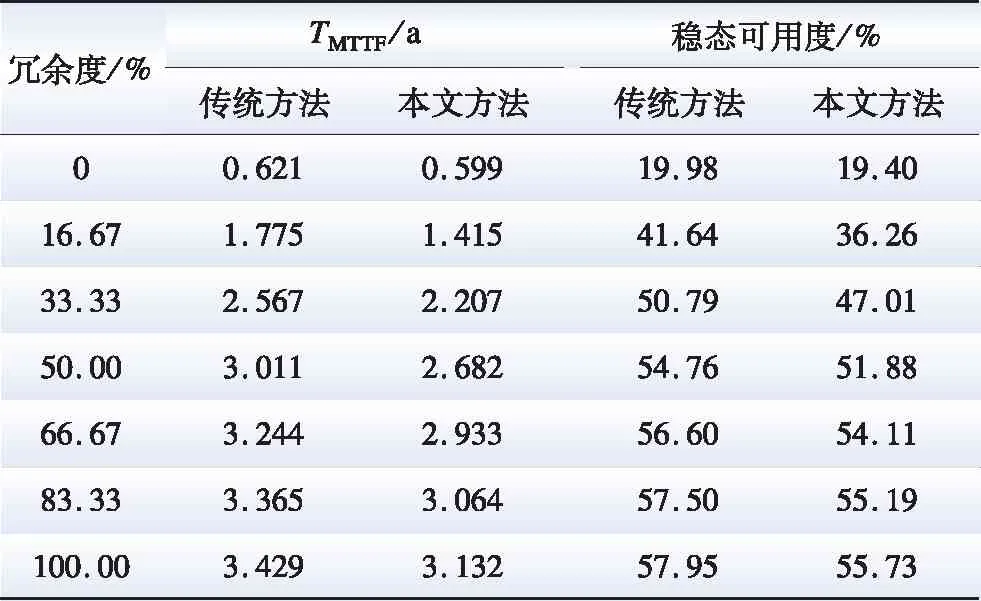
表3 半桥子模块冗余度的影响Table 3 The impact of redundancy

根据表3分析可知：

1)半桥子模块在冗余度为0时，故障率仍具备时变特性，这是由于MMC其他元件如控制保护系统、阀冷系统等仍具备一定的冗余度，导致未考虑故障率时变性时求解结果过于乐观；

2)随着半桥子模块冗余度由0升高至100%，在每一个冗余度下，本文方法所求TMTTF和稳态可用度均低于传统方法求解的计算结果，这是因为本文可靠性模型充分考虑了冗余系统故障率的时变特性对可靠性的影响，从而可靠性计算结果会偏低一些，提醒在工程应用中需要对冗余度进行谨慎考虑。

4 结 论

当MMC内部元件可靠度函数服从指数分布时，元件冗余会导致系统故障率时变，因此本文提出了一种考虑冗余系统时变故障率和更新过程的MMC可靠性建模方法，主要结论如下：

1)根据故障率定义公式可知，设备冗余系统故障率并非恒定，而是一个随时间单调递增的函数，默认MMC冗余系统的故障率恒定会导致其可靠性参数尤其为稳态可用度求解结果过于乐观；

2)MMC冗余系统时变故障率的增长速度随时间增长趋于0，因此N阶梯故障率与时变故障率契合程度较高，以N阶梯故障率代替MMC冗余系统时变故障率，在保证时变故障率均值增量Δλimp≤0.01次/a的精度范围内，利用短时间内故障率恒定的特点可求解MMC可靠性参数，与蒙特卡洛法相比，该方法计算量较少、计算结果较为保守；

3)和传统两状态马尔科夫模型相比，N阶梯更新过程的MMC可靠性模型所得TMTTF和稳态可用度较小，结果更为保守。

4)本文可靠性模型将冗余系统故障率时变性和更新过程建立了量化公式，修正了传统MMC可靠性参数计算结果偏高的问题，使可靠性计算结果更能反映MMC的真实可靠性。