含参数分数阶微分方程边值问题的极值解
吴怡敏, 沈钦锐
(闽南师范大学数学与统计学院, 福建 漳州 363000)
单调迭代结合上下解的方法已经成为研究微分方程特别是整数阶常微分方程边值问题的极值解存在性的一个有力工具.文献[1]中考虑了一类带参数的微分方程边值问题:

但是对于分数阶脉冲微分方程,利用单调迭代结合上下解方法研究其极值解的文献还是比较少.故为了更好地发展单调迭代方法,本文将分数阶的微分方程通过分数阶微积分理论转化为一阶常微分方程,然后利用一些解的比较结果得出了该分数阶微分方程的极值解的存在性.
本文考虑了如下一类带参数的分数阶脉冲泛函微分方程边值问题的极值解的存在性:
(1)

1 预备知识
引理1[1]函数f:J′→R的α>0阶Rieman-Liouille积分是指
引理2[1]对于Caputo型分数阶微分方程,当t∈(tk,tk+1],k=1,2,…,m时有
u(t)+c0+c1(t-tk)+…+cn-1(t-tk)n-1,
ci∈R,i=1,2,…,n,
其中,n=[α]+1.
考虑如下形式的线性微分方程
(2)


2 主要结果

(3)
定理21)称(x,λ)是(3)的一个下解,如果(x,λ)∈PC1[J,R]×R且满足
2)称(y,β)是(3)的一个上解,如果(y,β)∈PC1[J,R]×R且满足
引理3[2]假设u(t)∈PC1[J,R],p,q∈PC[J,R],dk≥0,bk∈R,使得
成立,则
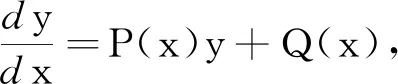
定理3若边值问题(3)的上解和下解分别是(v0(t),β0)、(u0(t),λ0),其中u0(t)、v0(t)是具有阶数为α的连续分数阶导数,并且有(v0(t),β0)≥(u0(t),λ0),t∈[-τ,T].假设下列条件成立:
(H1)对于任意的(x1,λ1),(x2,λ2)∈PC′[J×R,R],如果x1 -M(x-y)-N(xt-yt); 则问题(3)在序区间[u0,v0]×[λ0,β0]上有极大解和极小解.其中 [u0,v0]×[λ0,β0]={u∈PC[J,R]: u0≤u≤v0,λ∈R,λ0≤λ≤β,t∈[-τ,T]}. 证明若存在(u(t),λ)∈[u0,v0]×[λ0,β0]满足问题(3),则对任意(η,s)∈[u0,v0]×[λ0,β0],线性方程的初值问题 (4) 存在且有唯一解表示为 (5) G(η(T),s)-l(λ-s)=0有 (6) 证明当t∈[0,t1]时,由引理2得 由u(0)=k0,得c1=k0.所以当t∈[0,t1]时, 当t∈(t1,t2]时,由引理2得 由Δu(tk)=Ik(η(tk),s)-Lk[u(tk)-η(tk)]得 c2=I1(η(t1),s)-L1[u(t1)-η(t1)]+ 所以当t∈(t1,t2]时, 当t∈(tk,tk+1]时, 综上,(5)为问题(4)的解.下证唯一性. 先假设下列条件成立: (A1) 存在常数k1>0,k2>0使得不等式成立, 定义算子Φ:E→E,再令(5)式右边为Φu(t),则证明问题(4)解的唯一性转化为证明Φu(t)具有不动点,即Φu(t)=u(t). 令w(·):[-τ,0]→R,定义如下函数, (6) 等价.定义算子T:L1[J,R]→L1[J,R], (7) 由此算子Φ有不动点就转化为算子T有不动点. 对∀(z1,λ1)、(z2,λ2)∈L1[J,R]×R,t∈[0,T],当t∈[0,t1]时, |(Tz1)(t)-(Tz2)(t)|= 当t∈(tk,tk+1]时, |(Tz1)(t)-(Tz2)(t)|= 由(A2)知T是压缩映射算子,(7)有不动点,故(4)有唯一解. 定义算子A:[u0,v0]×[λ0,β0]→PC′[J,R]×R为A(η,s)=(u,λ),其中u,λ分别由(5)、(6)给出,若满足|f(tk,v(tk),β,vtk)-f(tk,u(tk),β,utk)|=Q(tk),则算子A有下述性质: 1) (u0,λ0)≤A(u0,λ0),A(v0,β0)≤(v0,β0); 2)A在[u0,v0]×[λ0,β0]上不减,即若(η1,s1)≤(η2,s2),则有A(η1,s1)≤A(η2,s2). 下证1),令(u1,λ1)=A(u0,λ0),p=u0-u1,则 p′(t)=u′0-u′1≤f(t,u0,λ0,u0t)+ f(t,u0,λ0,u0t)+M(u1(t)-u0(t))+ f(tk,u1(tk),λ1,u1tk)≤M(u1(t)-u0(t))+ N(u1t-u0t)+Q(tk)= -Mp(t)+N(u1t-u0t)+Q(tk),t∈J′, Δp(tk)=Δu0(tk)-Δu1(tk)≤ Ik(u0(tk),λ0)-Ik(u0(tk),λ0)+ Lk[u1(tk)-u0(tk)]=-Lkp(tk),k=1,2,…,m, p(0)=u0(0)-u1(0)≤0;p(t)=0,t∈[-τ,0]. 由引理1知p(t)≤0(t∈[-τ,T])成立. ①当p(t)<0时,u0 综上可得(u0,λ0)≤A(u0,λ0);同理可证A(v0,β0)≤(v0,β0). 下证2),记(ui,λi)=A(ηi,si),i=1,2.令p=u1-u2,则由(5)知 p′(t)=u′1-u′2=f(t,η1,s1,η1t)- f(tk,u1(tk),λ1,u1tk)-f(t,η2,s2,η2t)-M(u2(t)- f(tk,u2(tk),λ2,u2tk)≤M(η2-η1)+ N(η2t-η1t)-M(u1(t)-u2(t))+M(η1(t)-η2(t))-N(u1t-u2t)+N(η1t-η2t)+Q(tk)≤ -Mp+N(u2t-u1t)+Q(tk),Δp(tk)=Δu1(tk)- Δu2(tk)=Ik(η1(tk),s1)-Lk[u1(tk)-η1(tk)]-Ik(η2(tk),s2)+Lk[u2(tk)-η2(tk)]≤-Lkp(tk), p(0)=u1(0)-u2(0)=k0-k0=0, p(t)=0,t∈[-τ,0]. 由引理1得p(t)≤0,t∈[-τ,T]. ①当p(t)<0时,u1 ②当p(t)=0时,u1=u2,由0=G(η1(T),s1)-l(λ1-s1)-G(η2(T),s2)+l(λ2-s2)≤-l(λ1-λ2),知λ1≤λ2. 综上A(η1,s1)≤A(η2,s2). 利用上述类似讨论,使用归纳的方法得到一个关于问题(3)上下解序列{un(t),λn}、{vn(t),βn}并且(un+1,λn+1)=A(un,λn)、(vn+1,βn+1)=A(vn,βn),n=0,1,2….则由1),2)得(u0,λ0)≤(u1,λ1)≤…≤(un,λn)≤…≤(vn,βn)≤…≤(v1,β1)≤(v0,β0),并且由(4)、(5)、(6)知上述上下解序列具有如下定义: (8) (9) 且易知(8)、(9)的解为: 由于序列{un(t),λn}单调不减有上界,序列{vn(t),βn}单调不增有下界,可得序列{un(t),λn}、{vn(t),βn}分别在[0,T]上一致收敛,记 由f、G的连续性及(8)、(9)知当n→∞时,(u,λ),(v,β)都是问题(3)的解.下证(u,λ),(v,β)分别是问题(3)的极小解和极大解.令(η,s)∈[u0,v0]×[λ0,β0]是问题(3)的任一解.要证 (u,λ)≤(η,s)≤(v,β),t∈[0,T], 首先(u0,λ0)≤(η,s)≤(v0,β0)对任意t成立.假设对于n∈N,式(un,λn)≤(η,s)≤(vn,βn)成立. 令x(t)=un+1-η,由(8)和(3), x′(t)=u′n+1-η′=f(t,un,λn,unt)- f(tk,un+1(tk),λn+1,un+1,tk)-f(t,η,s,ηt)- M(η-un)+N(ηt-unt)-M(un+1-un)- N(un+1,t-unt)+Q(tk)= -Mx(t)+N(ηt-un+1,t)+Q(tk), Δx(tk)=Δun+1(tk)-Δη(tk)=Ik(un(tk),λn)-Lk[un+1(tk)-un(tk)]-Ik(η(tk),s)≤Lk[η(tk)-un(tk)]-Lk[un+1(tk)-un(tk)]=-Lkx(tk),k=1,2,…,m, x(0)=un+1(0)-η(0)=0; x(t)=0,t∈[-τ,0], 由引理1得x(t)≤0,t∈[-τ,T]. ①当x(t)<0时,un+1<η,则(un+1,λn+1)<(η,s)成立. ②当x(t)=0时,un+1=η,由 0=G(un(T),λn)-l(λn+1-λn)-G(η(T),s)≤-l(λn+1-s), 知λn+1≤s.综上(un+1,λn+1)≤(η,s)成立.同理可证(η,s)≤(vn+1,βn+1),故有(un+1,λn+1)≤(η,s)≤(vn+1,βn+1),再由数学归纳法可知(un,λn)≤(η,s)≤(vn,βn)对任意的n∈N都成立.令n→∞得(u,λ)≤(η,s)≤(v,β),t∈[0,T].因此,问题(3)在[u0,v0]×[λ0,β0]上有极大解(v,β)和极小解(u,λ),即问题(1)在[u0,v0]×[λ0,β0]上有极大解(v,β)和极小解(u,λ),证毕. 例1考虑如下含参数分数阶微分方程边值问题: (10) 易知(10)等价于 (11) f(t,v,λv,vt)-f(t,u,λu,ut)= λvv-λuu-sint(vt-ut)≥ λu(v-u)-sin 1(vt-ut),
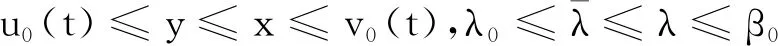
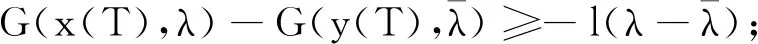
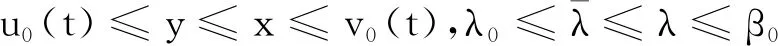






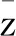



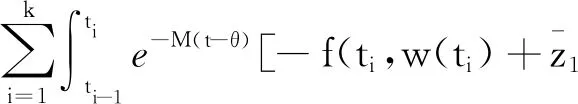
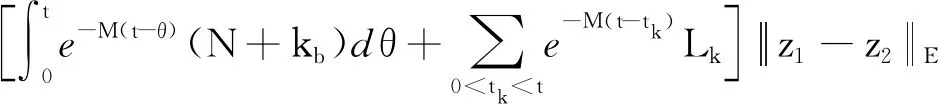
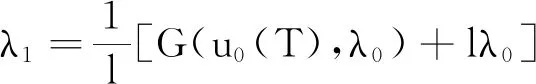

3 实例