用移动粒子半隐式方法数值模拟Poiseuille 流动问题
兰小杰,赵伟文,万德成
1 上海交通大学 船海计算水动力学研究中心,上海 200240
2 上海交通大学 船舶海洋与建筑工程学院,上海 200240
0 引 言
Poiseuille 流动问题广泛存在于工业生产中,其最典型的例子是低雷诺数时的管道流动。近年来,随着在深海资源开采方面的竞争越来越激烈,矿物管道输运系统作为深海采矿的关键环节,对其的研究需求愈发迫切。而针对Poiseuille 流动的机理研究对于更复杂的管道运输问题来说具有一定的指导意义。
早在19 世纪,Hagen 和Poiseuille 就从实验中归纳出了低雷诺数圆管中的液体层性管流规律,即圆管截面上的速度分布为抛物线分布[1]。1968 年,Fox 等[2]通过实验对Poiseuille 流的稳定性进行了研究,发现当雷诺数Re> 2 150 时,Poiseuille 流开始出现失稳现象。Papanastasiou 等[3]使用分离变量的方法求得了Poiseuille 流问题的理论解。陈雷等[4]对不同边界条件下的非稳态不可压缩Poiseuille 流的发展过程进行了研究,发现对于平均速度随着时间从0 线性增加边界、恒压力边界、恒平均速度边界这3 种不同类型的边界条件,对应的非稳态发展过程依次缩短。金开文等[5]使用格子Boltzmann 方法对Poiseuille 流进行了模拟研究,发现模拟结果与理论结果吻合,说明采用格子Boltzmann 方法处理压力驱动类层流问题具有可行性。在粒子法方面,Adami 等[6]采用光滑粒子流体动力学方法( SPH)对Re=0.001 25 时的二维Poiseuille流进行了模拟,发现模拟结果与理论结果吻合较好,证明采用SPH 方法模拟低雷诺数下的Poiseuille 流是有效的。Meister 等[7]利用弱可压缩SPH 方法对Poiseuille 流进行了模拟,发现将SPH 方法应用于中、高雷诺数下的Poiseuille 流(Re≥ 1)会导致横向不稳定性问题,并对造成这种不稳定性的原因进行了探讨。刘谋斌和常建忠[8]采用SPH 方法模拟了Poiseuille 流,发现其稳定一段时间后会出现模拟结果逐渐偏离稳定解的情况,说明采用原有SPH 方法模拟Poiseuille 流会存在数值不稳定的情况,然后采用一种改进的SPH 方法— 有限粒子法模拟了Poiseuille 流,结果发现数值不稳定的情况消失了,可见,有限粒子法是解决原有SPH 方法数值不稳定的一个有效方法。Song 等[9]利用SPH 方法对Re= 0.01~100 下的Poiseuille 流进行了模拟,系统地研究了参数、背景压力、初始粒子密度和密度重新初始化技术对SPH 模拟Poiseuille 流的影响。综上所述,粒子法对Poiseuille 流的研究大多集中在SPH 方法上,鲜有人采用移动粒子半隐式(moving particle semi-implicit,MPS)方法对Poiseuille流进行研究。
1996 年,Koshizuka 和Oka[10]在SPH 方法的基础上提出了MPS 方法,主要用于模拟不可压缩流动问题。与网格类方法最大的不同之处是,在MPS 方法中,流体是通过相互作用的粒子来离散的,并利用拉格朗日粒子携带空间流场的信息,粒子之间的影响则通过核函数来实现。由于粒子运动不会受到网格间固定拓扑关系的限制,因此在处理大变形的自由面问题时不会出现网格畸变的问题,具有更大的灵活性。粒子法目前已被广泛应用于自由表面的流动,以及多相流和水下爆炸等流动中[11-16],但将其应用于壁面剪切流动时的数值稳定性还需进一步予以验证。为此,本文将使用MPS 求解器MLParticle-SJTU,通过建立恒流量入口边界条件和无滑移壁面边界条件,模拟二维Poiseuille 流并与理论解析解进行对比,验证MPS 方法在模拟Poiseuille 流问题上的有效性。
1 数值方法
1.1 控制方程
在MPS 方法中,控制方程一般包括连续性方程以及N-S 方程,分别可以写成如下形式:
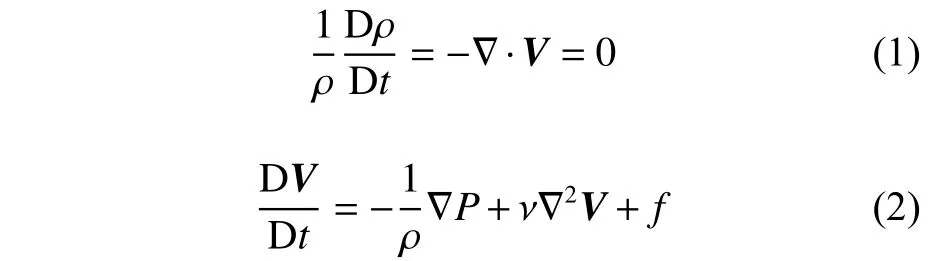
式中:ρ 为流体密度,m3/kg;V为流体速度矢量,m/s;P为流体压力,Pa; ν为流体运动黏性系数,m2/s;f为流体质量力,m/s2。
1.2 核函数
有别于SPH 方法,MPS 方法中的核函数只是作为权函数来使用,其求解过程无需使用核函数的导函数,所以MPS 方法的核函数只要求连续而不要求光滑。本研究采用的核函数为文献[15]推荐的核函数,表达式如下:
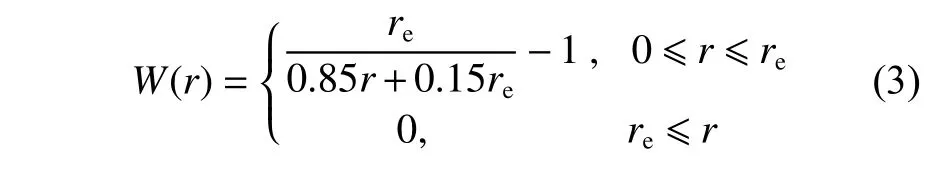
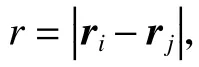
1.3 不可压缩条件
本文采用Lee 等[17]改写的混合源项法,表达式如下:
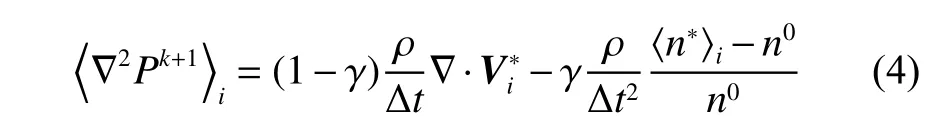
式中:γ 为泊松方程源项中粒子数密度的权重,可取0~1 之间的任意数值,本文取γ = 0.99;为粒子i的临时速度矢量; 在MPS 方法中,通常使用粒子数密度来表示粒子的疏密,n0为初始粒子数密度,n*为临时粒子数密度。<n*>的表达式如下:
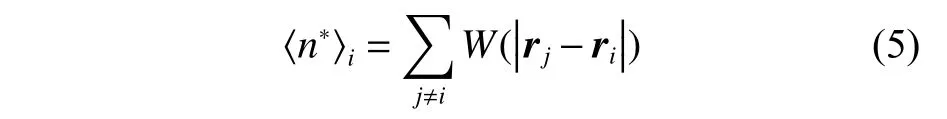
1.4 梯度模型
本文采用的梯度模型为:
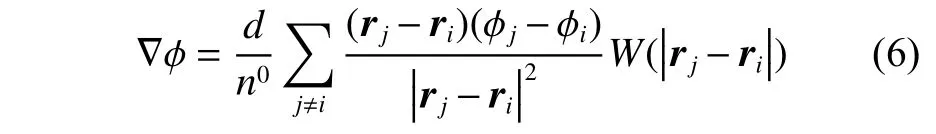
式中: φ为任意标量, φi和 φj为此标量在粒子i,j处的值;d为计算维数,本文研究的是二维Poiseuille 流。
1.5 散度模型
在连续性方程中存在散度项,需使用核函数对散度项进行离散。本文采用的散度模型为:

式中, Π为任意矢量, Πi和 Πj分别为粒子i,j处该矢量的值。
1.6 Laplacian 模型
本文使用Koshizuka 和Oka[10]所给的如下Laplacian 模型:
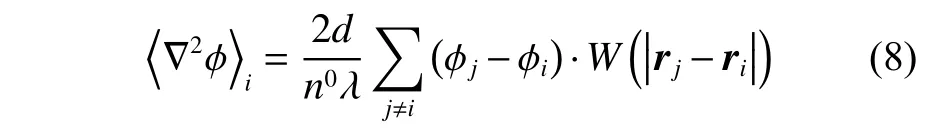
式中,λ 为修正系数。引入λ 可以修正数值计算的结果,使其与扩散方程的解析结果一致,其表达式为:
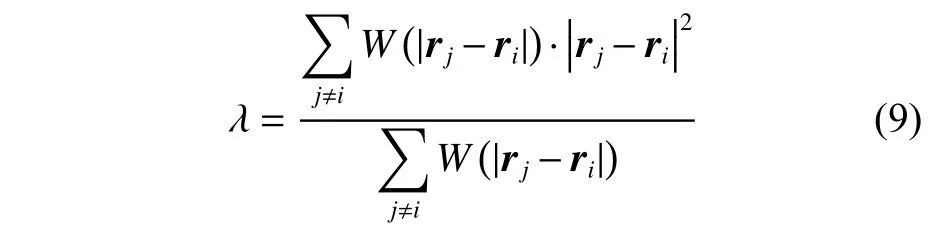
1.7 边界条件
如图1 所示,入口采取推板的形式形成恒流量入口,推板向前推动流体流动,在到达指定的位置后,推板退回至初始位置,再在空出的位置填入幽灵粒子,并赋予它们质量、黏性、密度等与流体相关的物理量,使其转换成流体粒子。将从出口流出计算域的流体粒子转换成幽灵粒子,在入口推板后退时填入入口处,并重新转换回流体粒子,幽灵粒子的质量、密度等物理量均为0。MPS 方法中的壁面边界由多层粒子组成,与流体颗粒相邻的边界粒子为第1 类边界粒子,其压力通过压力Poisson 方程得到;不与流体粒子接触的粒子为第2 类边界粒子,其压力通过周围流体粒子和第1 类边界粒子向外插值得到。
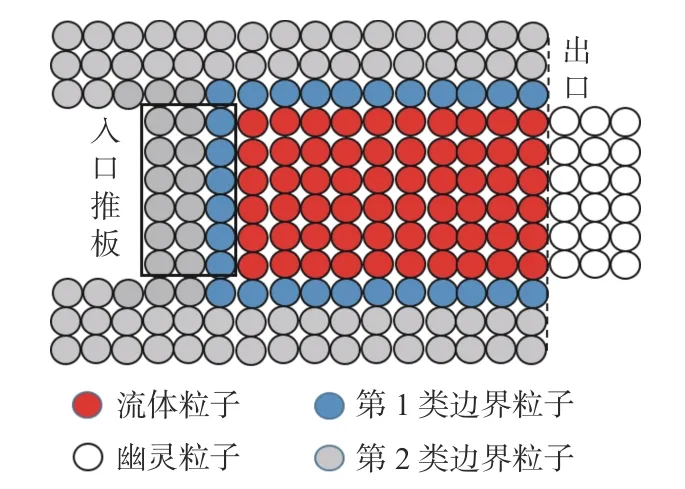
图1 边界示意图Fig. 1 Schematic diagram of boundaries
上、下边界均设置为不可滑移壁面,图2 所示为无滑移壁面示意图。图中:Ui,u⊥,u||分别为流体粒子的速度、垂直于壁面的速度和平行于壁面的速度;′分别为与流体粒子对应的虚拟粒子的速度、垂直于壁面的速度和平行于壁面的速度,这些速度的单位均为m/s。在每个时间步内计算黏性力时,在壁面外侧生成虚拟粒子,虚拟粒子与流体粒子关于壁面轴对称。在无滑移壁面条件下,当壁面静止时,虚拟粒子的垂向速度和切向速度均与流体粒子相反;在计算黏性力时,需考虑这些虚拟粒子对流体粒子的作用力,从而形成无滑移壁面边界条件。
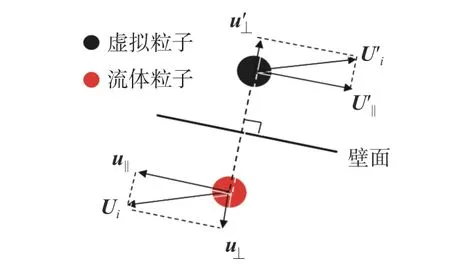
图2 不可滑移边界示意图Fig. 2 Schematic diagram of no-slip boundary
2 数值模拟
2.1 Poiseuille 流
所谓Poiseuille 流,是指由压力驱动的层性管流,在流动充分发展后,截面上的速度分布将呈抛物线形状,如图3 所示。图中,D为管道直径。
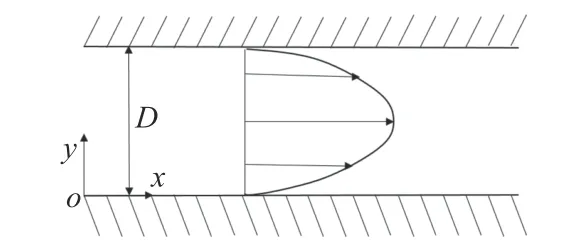
图3 Poiseuille 流示意图Fig. 3 Schematic diagram of Poiseuille flow
由于Poiseuille 流动条件简单,其基本方程组可以有解析解,解析解如下:
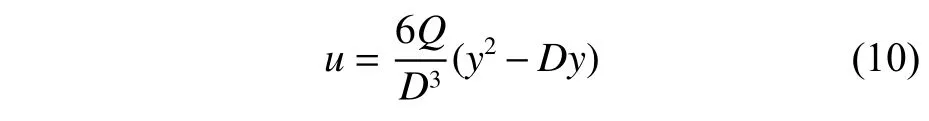
式中:u为流体在x方向的速度;Q为流量。由式(10)可以看出,Poiseuille 流的速度分布呈抛物线形状,通过流速的分布,可以验证后续经MPS 方法模拟得到的结果。
2.2 计算模型
图4 所示为计算域的示意图。设D= 0.2 m,为了让流动能够充分发展,将计算流体域的长度设置为15D。此外,设流体的密度ρ= 1 000 kg/m3,黏性系数μ= 0.001 Pa·s。计算工况包括3 个,即入口速度U= 0.000 02,0.000 2 和0.002 m/s,其雷诺数Re= 4,40,400。
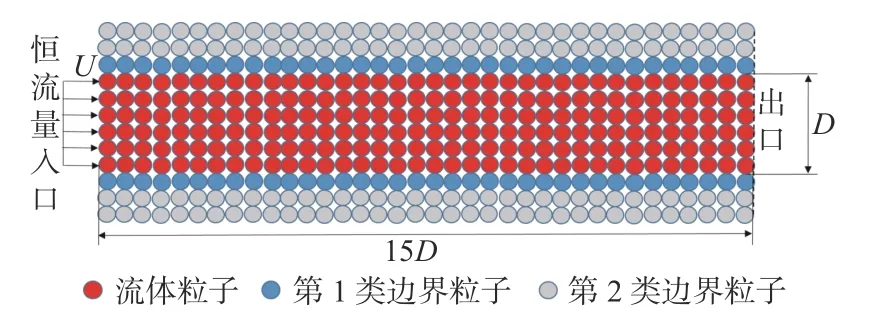
图4 计算域示意图Fig. 4 Schematic diagram of computational domain
2.3 收敛性分析
选取Re= 400 的工况,采用3 种不同的粒子间距dx= 0.005 5,0.004 和0.002 5 m 来对粒子的收敛性进行验证,3 种粒子间距对应的流体粒子数量分别为18 410,36 750 和94 800。图5 对不同粒子间距下流动充分发展后的截面速度分布与解析解进行了对比,图中,y/D为截面纵坐标与管道直径的比值。由图可见,不同粒子间距对应的截面最大速度分别为Vx= 0.002 62,0.002 875,0.002 822 m/s,与解析解的差距分别为12.7%,4.0%和5.9%;dx= 0.004 m 与dx= 0.002 5 m 的计算结果十分接近,说明当dx达到0.004 m 后,继续减小粒子间距对模拟结果的影响很小,考虑到计算量,接下来的工况将均选取dx= 0.004 m 来进行相关计算。
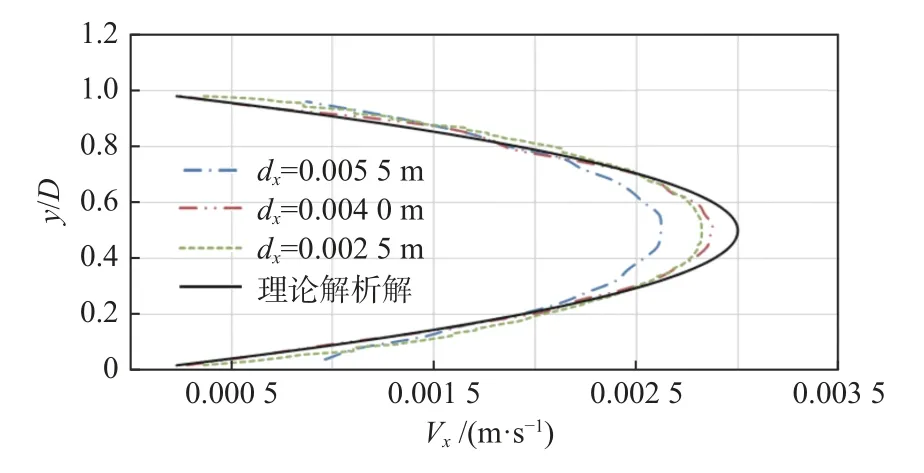
图5 Re = 400 时不同粒子间距下截面x 方向的速度分布Fig. 5 Velocity distribution of flow in the x direction in different dx when Re = 400
2.4 模拟结果
图6 所示为不同雷诺数下,流动充分发展后流体域在x方向的速度云图。从图中可以看到,在无滑移壁面及流体黏性的作用下,3 个工况下的速度均呈现出上下界面的速度小、中间的速度最大的规律。图7 所示为不同雷诺数下流动充分发展后中心线上的速度分布,图中Vx/U为x方向速度与入口速度的比值。从中可以看到,随着Re的增加,流动充分发展所需长度也随之增加,即Re= 4,40,400 时流动充分发展所需长度分别约为1.5D,2.5D和10D。
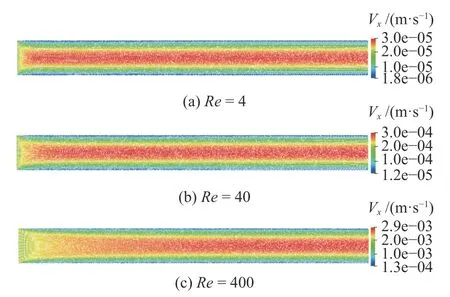
图6 流体域在x 方向的速度云图Fig. 6 Velocity contours of fluid domain in the x direction
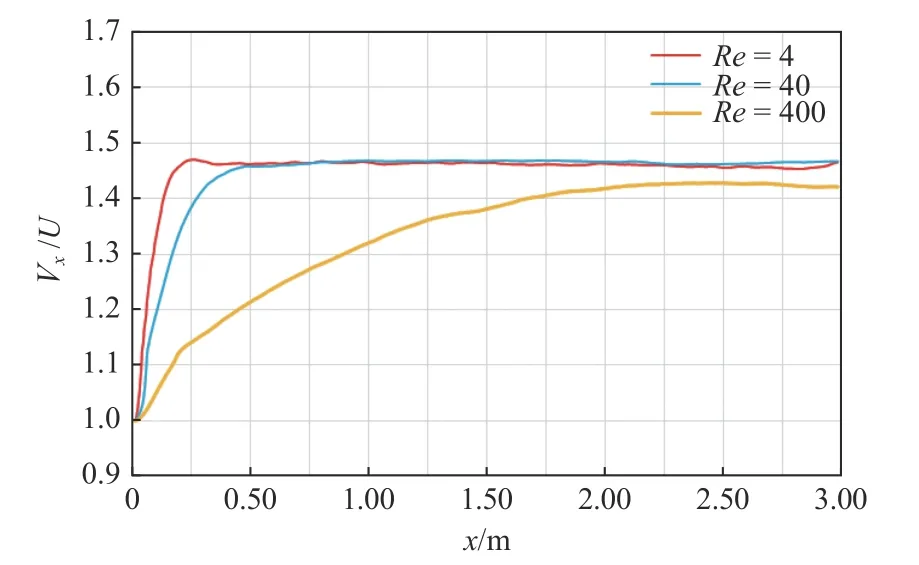
图7 流动充分发展后在中心线上x 方向的速度分布Fig. 7 Velocity distribution of fully-developed flow on the central axis in the x direction
选取x=10D的截面,观察截面处x方向的速度分布随时间的变化,如图8 所示。由图可见,在不同工况下及流动发展的初始阶段,截面不同位置处的流速差均较小;随着流动的发展,中间位置的流速不断增大;待流动充分发展后,速度剖面曲线最终呈抛物线形状。在Re= 4 工况下,当无量纲时间Ut/D= 0.5 时,速度剖面曲线与理论解析解几乎重合,此时流动发展到稳定状态,至Ut/D= 10 时,截面的速度峰值有所回落,其值略小于理论解析解,相对误差为2.6%,不过也只是在理论解析解附近有小幅度的振荡,未有完全偏离稳定解的情况,说明采用MPS 方法模拟Poiseuille流动问题不存在数值不稳定现象。在Re= 40 工况下,当Ut/D= 2 时,截面处x方向的速度分布与Ut/D= 10 时的几乎完全一致,说明流动已充分发展,此时截面处的最大速度Vmax= 0.000 293 4 m/s,略小于0.000 3 m/s 的理论解析解,相对误差为2.1%。在Re= 400 时,Vmax= 0.002 875 m/s,与解析结果间的相对误差为4.0%。
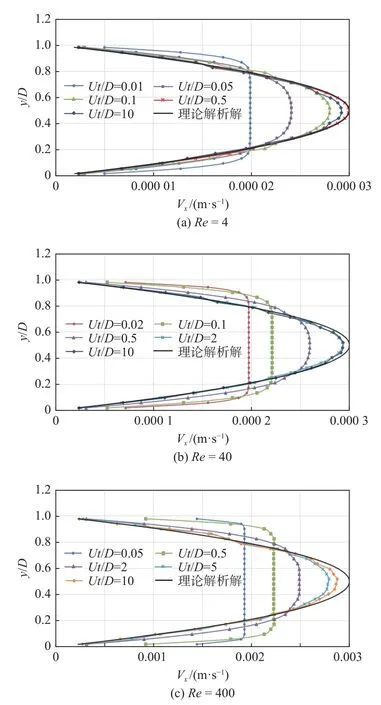
图8 x = 10D 截面处x 方向的速度分布随时间的变化Fig. 8 Velocity distribution of flow in the x direction changes with time at the section of x = 10D
在MPS 方法中,粒子按拉格朗日描述法进行自由运动,其可以跟踪粒子每个时间步的位置。选取Re= 4 的工况,跟踪初始时刻x方向位置在x= 10D截面处流体粒子的运动,图9 所示为其在不同时刻的分布形状。从中可以看到,在初始时刻,同一截面处的粒子由于运动速度不一致,随着时间的发展会呈现抛物线形状。
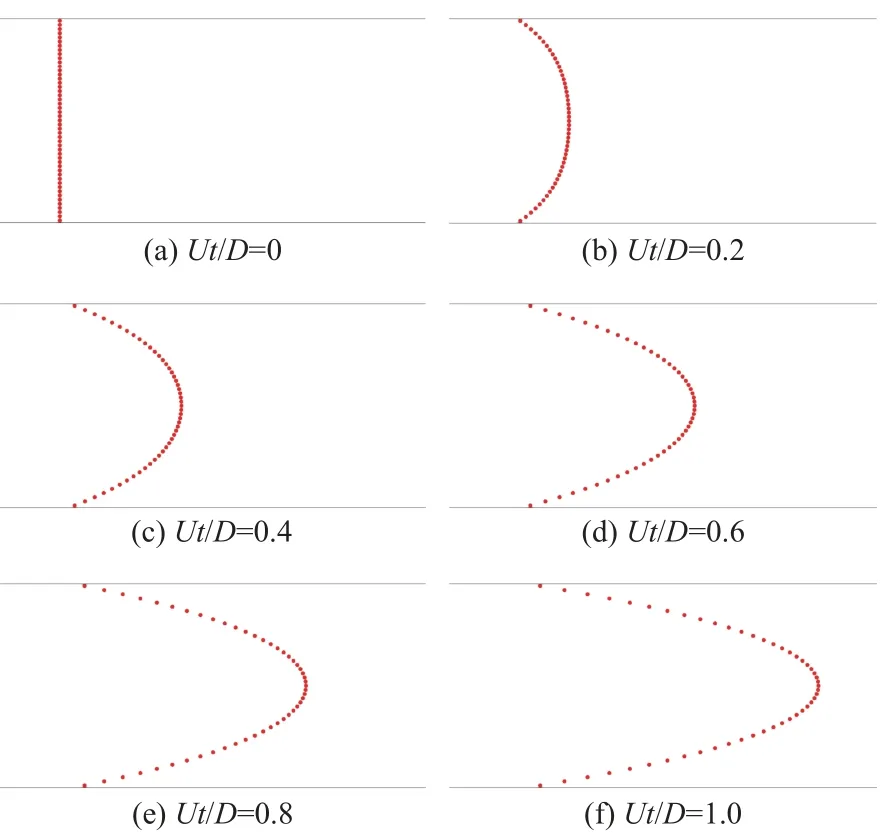
图9 Re = 4 工况下在初始时刻x = 10D 截面处粒子随时间的变化分布Fig. 9 Distribution of particle moves with time at the section of x =10D at initial time when Re = 4
3 结 语
本文运用MPS 方法,建立了出入口边界及无滑移壁面条件,并对不同雷诺数下的二维Poiseuille流进行了模拟。计算结果表明:Poiseuille 流充分发展后,流体速度的分布情况是从中间向两侧逐渐递减,速度分布呈抛物线形状,且在恒流量入口边界条件下,随着雷诺数的升高,Poiseuille 流发展所需要的流动长度变大;在不同雷诺数下,Poiseuille 流经充分发展后,模拟得到的速度最大值与理论解析解之间的相对误差在5%以内,验证了采用MPS 方法模拟Poiseuille 流问题的可靠性及有效性。下一步,将对采用MPS 方法模拟相对更复杂的柱体绕流相关问题的可靠性进行计算与验证。

