一类具扩散的HBV模型的稳定性分析

甘文珍，金龚逸，袁 樱

（江苏理工学院 数理学院，江苏 常州 210331）

众所周知，传染病因其具有传染性严重威胁着人类的生命和健康。乙肝病毒（HBV）感染作为全球性的公共卫生问题，已经得到广泛的关注和研究，特别是传染病动力学的介入使HBV的防治进入了新的阶段。早在1927年，Kermack和Mckendrick[1]为了研究瘟疫和黑死病的传播机制，建立了经典的SIR仓室模型，成为传染病动力学的基础。Nowak等人[2]根据HBV的特点，于1996年首次提出了如下HBV动力学模型：

其中：x,y,v分别表示健康肝细胞、染病肝细胞和自由病毒的密度；λ和d分别表示健康肝细胞的产生速率和死亡速率；c表示染病肝细胞的治愈率；b表示自由病毒的死亡率。在没有免疫反应的条件下，健康肝细胞按照βxv的双线性方式感染，染病肝细胞以a的速率死亡。随后，Korobeinikov[3]利用Lyapunov函数证明了：当R0<1时，无病平衡点全局渐近稳定；当R0>1时，染病平衡点全局渐近稳定。

随着病毒研究的深入，HBV的更多特点被进一步发现，因此很多学者对早期提出的基础模型进行了改进。譬如：Nowak等人[4]通过添加免疫反应项，建立了具有免疫反应的HBV模型系统；Hews等人[5]考虑了健康肝细胞的Logistic增长和标准发生率，在模型（1）的基础上建立了如下模型：

其中：r表示增长率，K表示环境容量；健康肝细胞的转化率为，其中β表示接触率；a，γ表示染病肝细胞的死亡率和治愈率，μ表示自由病毒的死亡率。Manna等人[6]着重考虑了HBV-DNA衣壳，建立了一类HBV动力学模型系统，并分析了其正平衡点的局部渐近稳定性和全局渐近稳定性。近期，Gharahasanlou等人[7]提出了一般发生函数下具有CTL免疫的HBV系统，即：

其中，z表示CTL的细胞密度。Gharahasanlou等人[7]对文献[4，8，9]中的发生函数进行了推广，利用Lyapunov函数证明了各正平衡点的全局稳定性。

以上模型系统均假设健康肝细胞、染病肝细胞和自由病毒在空间上是没有随机移动的。可事实上，这种随机移动在许多生物现象活动中扮演着重要的角色。Funk等人[10]采用了一个补丁模型来模拟病毒向最近邻居的移动，即扩散。假设健康肝细胞和染病肝细胞在正常环境下是不能移动的，但自由病毒在肝脏中可以随机移动，且自由病毒的扩散遵循Fick扩散。据此，Wang等人[11]提出了一个具扩散的HBV模型，讨论了该模型行波解的存在性。Xu等人[12]建立了一个具有饱和发生率的时滞扩散模型，并研究了正平衡点的局部渐近稳定性和全局渐近稳定性。在文献[6]的基础上，Manna等人[13]通过引入扩散项，建立了一类具扩散的时滞HBV模型，并研究了正平衡点的局部渐近稳定性和全局渐近稳定性。

受以上研究的启发，本文在模型（2）的基础上考虑自由病毒的扩散，建立如下的反应扩散方程组：

其中：Ω是RN中的有界区域，边界∂Ω光滑；η是边界上的单位外法向量；u1,u2,u3表示健康肝细胞、染病肝细胞和自由病毒在t时刻的空间分布密度；d表示扩散率；ϕi是Ω上连续的非负函数。本文主要讨论模型（4）解的渐近行为，安排如下：第一节讨论无病平衡点和染病平衡点的局部渐近稳定性；第二节证明无病平衡点的全局渐近稳定性；第三节利用数值模拟呈现所得结论。

1 无病平衡点和染病平衡点的局部渐近稳定性

由标准偏微分方程理论可知，模型（4）的解存在且唯一，下面给出解的先验估计。

定理1：对于任何非负初值函数，模型（4）有唯一全局解(u1,u2,u3)，且在Ω×( 0,+∞)内满足。其 中，

定理2：当时，模型（4）仅存在无病平衡点。当时，模型（4）除了存在无病平衡点外，还存在唯一的染病平衡点其中：表示细胞存活指数。

下面，利用线性化方法和特征值理论讨论模型（4）平衡点的局部渐近稳定性。利用文献[14]中的方法，设0=μ1<μ2<…是Ω中带有齐次Neumann边界条件的算子-Δ的特征值，是中对应于μi的特征子空间。令是的标准正交基，令模 型（4）在处 的 线 性 化 方 程 为其中：的特征值。故模型（4）的特征方程为：

定理3：当R0<1时，无病平衡点Ef局部渐近稳定；当R0>1时，无病平衡点Ef不稳定。

证明：根据以上分析，模型（4）在Ef=( )

K,0,0处的特征方程为：

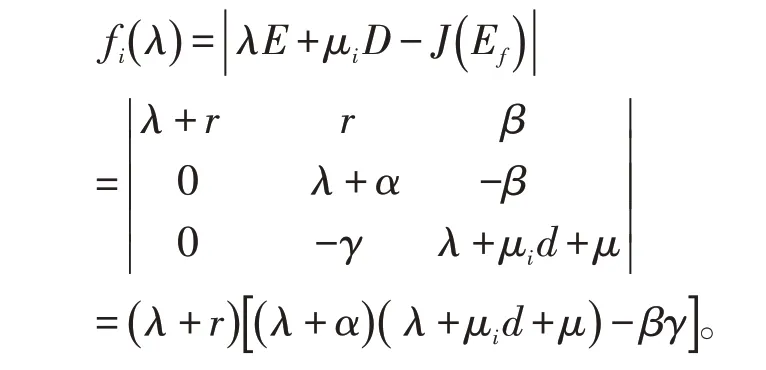
对每个i≥1,Xi是算子L的不变子空间，因此λ是L在Xi中的特征值，当且仅当它是矩阵

经过计算得到特征根为：

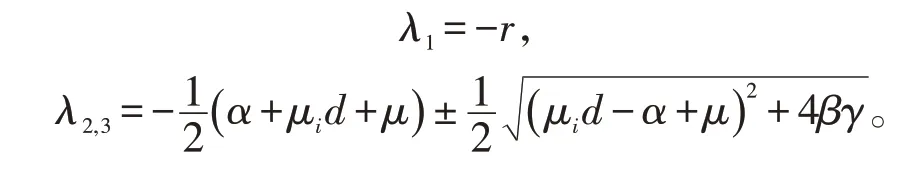
容易判断λ1<0。当R0<1时，有：

因此，λ2,3是负根。

下证R0>1时，无病平衡点的稳定性。

当i=1，μ1=0时，特征方程为：

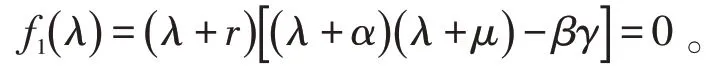
当λ→∞时，f1()λ→∞。当R0>1时，方程f1(λ)=0至少包含一个正根，L的谱包含了一个Reλ>0的特征值。由文献[14]的推论1.11可知，当R0>1时，无病平衡点Ef是不稳定的。

定理4：当时，染病平衡点E*局部渐近稳定。

证明：模型（4）在处的特征方程为：

经计算可得：

其中：

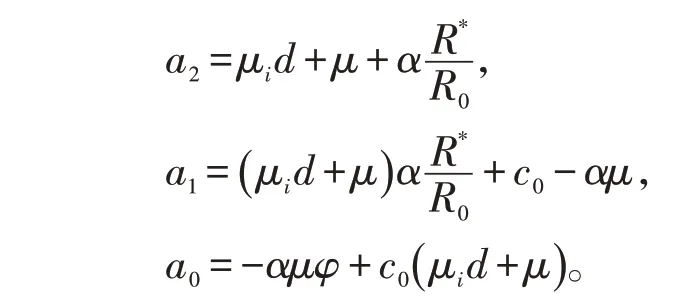
显然，a2>0，当时，有：

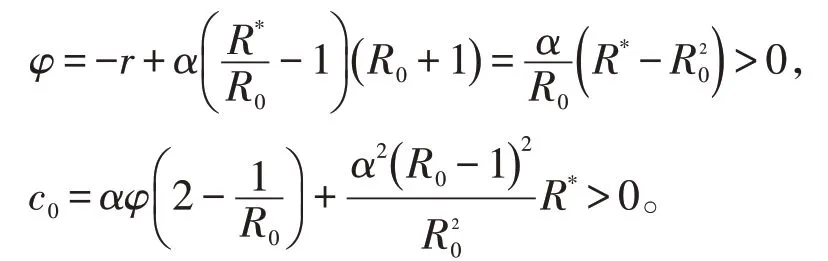
因此，

令Δ=a1a2-a0，则有：

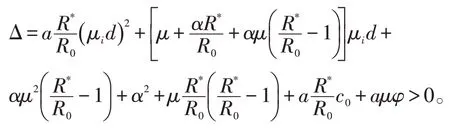
根据Routh-Hurwitz判别条件可知，式（5）的根具有负实部。进一步令λ=μiζ，则式（5）变为：

当i→∞时，有μi→∞，故：

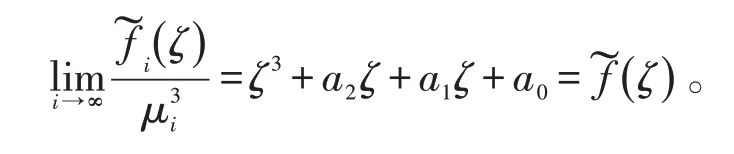
因为，a0，a1，a2>0，且a1a2-a0>0，故 由Routh-Hurwitz判别条件得知的 三 个根ζ1，ζ2，ζ3均 有 负 实 部，即 存 在-δ，使 得由 连 续 性 可 知，存 在i0∈N使 得 方 程的 三 个 根ζi,1，ζi,2，ζi,3

2 无病平衡点的全局渐近稳定性

在讨论无病平衡点Ef的全局稳定性之前，首先给出一个重要的引理。

引理1[15]：设a，b为正常数，，且ϕ有 下 界。如 果，且在上对某些正常数K成立，则

定理5：当R0<1时，无病平衡点Ef全局渐近稳定。证明：对于，定义Lyapunov函数为：

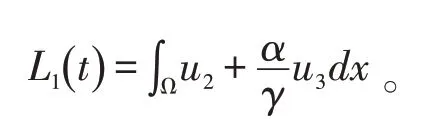
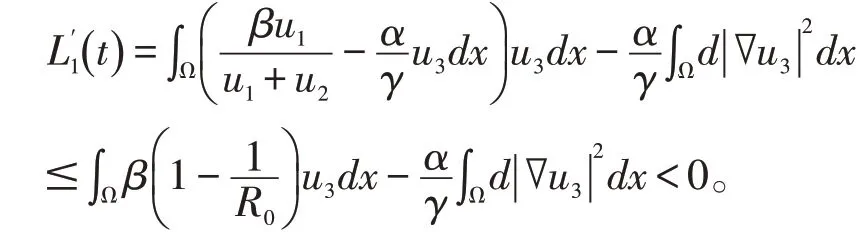
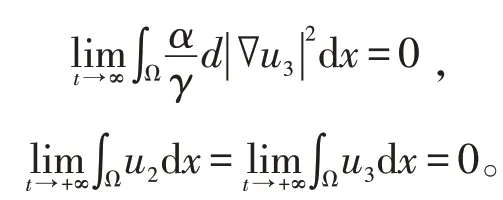
由Poincaré不等式知：

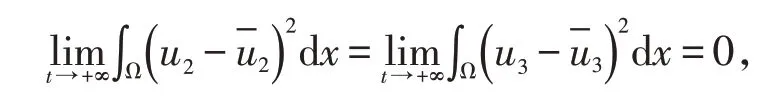
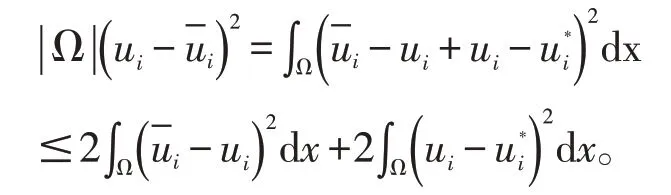
注：当接触率很小时，该疾病将不会流行。

3 数值模拟

对模型（4）进行数值模拟，取以下两组参数。

例1：取参数r=1,K=2e11，d=4，α=0.069 3,β=0.001 4，γ=25，μ=0.693。

并取初值函数：

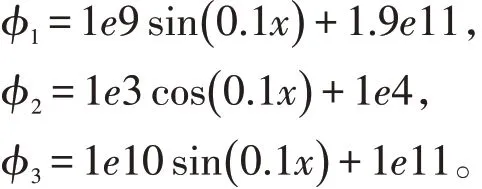
经过计算，R0=0.728 8<1，满足定理3和定理5的条件，故在该组参数下无病平衡点Ef(2e11,0,0)是全局渐近稳定的。由图1可知，当时间t趋于无穷时，健康肝细胞数量达到环境容量K，染病肝细胞和自由病毒数量为0，传染病最终会消亡。

图1 无病平衡点Ef的全局稳定性

例2：取参数r=1,K=2e11，d=4，α=0.069 3,β=0.001 4，γ=25，μ=0.693。

并取初值函数：

图2 染病平衡点E*的全局稳定性