Dynamic transport characteristics of side-coupled double-quantum-impurity systems

Yi-Jie Wang(王一杰) and Jian-Hua Wei(魏建华)

Department of Physics,Renmin University of China,Beijing 100872,China

Keywords: quantum dots,tunneling transition,capacitive type

1. Introduction

Quantum dots can form different quantum-impurity systems with different leads as a typical low-dimensional mesoscopic system(metal lead, ferromagnetic lead, superconducting lead, etc.), which serves as a more detailed research tool in the field of strong correlation. Since a double-quantumimpurity system possesses a variety of geometrical configurations, its tunneling path is more than that of the singlequantum-impurity system, and thus there are more abundant physical properties belonging to double-quantum-impurity systems. The Aharonov-Bohm oscillation, Fano resonance,Kondo effect,quantum phase transition,thermoelectric effect are a few of examples.[1-10]Research on transport properties of double-quantum-impurity systems not only provides a theoretical basis for the study of integrated circuits but also plays a vital role in the study of quantum bit, quantum regulation,and other aspects.[11]

Although many studies have been made on the spatial coherence of the electron wave function in quantum-impurity systems, the temporal coherence of the same system remains to be studied due to the difficulties involved in dealing with the time phase coherence and time memory effect of the electrons.[12,13]There have been many studies on the transport properties of quantum-impurity systems. For example,for a system having no interaction, the traditional Landauer-Buttiker scattering matrix theory provides steady state current through the leads.[14,15]Wingreenet al. studied the timedependent transport current using the method of motion equation for the first time and gave the analytical expression of current using Keldysh Green’s function and Dyson’s equation.Such oscillation behavior of time-dependent current has gathered people’s attention.[16,17]However, this method relies on wide-band limit(WBL),and its shortcoming is that when electricity has very limited bandwidth or energy-dependent state density, it cannot calculate the transport current of the system quantitatively and accurately. Zhuet al. used the timedomain decomposition method to directly calculate the timedependent transport currentI(t)in the numerical form by using Green’s function. However, this method has difficulty in accurately solving the case of weak coupling between the device and the lead.[18]Maciejkoet al. theoretically provided an exact analytical expression for the transport current under nonequilibrium and nonlinear response conditions, whereas this expression needs to be derived once again after the step voltage applied to the leads is changed.[19]From most studies made on the dynamic transport current of quantum-impurity systems,it can be seen that electron-electron(e-e)interaction is either ignored or treated in the mean field.

Some studies have been conducted on quantum-impurity systems despite having difficulty in calculation of timedependent transport current. For example, the density matrix renormalization group method is extended to time-varying to deal with time-dependent one-dimensional systems and the transport problems of single impurity systems.[20-22]The time-dependent numerical renormalization group method was used for studying the nonequilibrium dynamics of quantumimpurity systems, and it was found that the occupancy number would appear as Rabi oscillation when the time-dependent gate voltage was applied on the quantum-impurity.[23,24]However, the use of perturbation processing has not been able to accurately describe the latest physical phenomena, and the above work focuses on single-level resonant tunneling,which does not aptly explain the interesting phenomenon of timedependent transport characteristics in the Kondo system.

In the present study, we investigate the nonequilibrium dynamics of quantum impurity systems based on the hierarchical-equations-of-motion (HEOM) approach, taking into account the environmental effects. The time-dependent quantum transport problem is solved by using a series of equations of motion to calculate the time-dependent transport current of the quantum-impurity systems with the help of a nonperturbed quantum impurity model.These are all related to the experiments on quantum dots and quantum wires, which are of great significance for quantum computation in the abovementioned nanometer devices.

Recently, our group has carried out some research based on this method. One is related to the tunneling coupling between quantum dots. We pointed out that the temperature inhibits the oscillation of dynamic current by inhibiting kondo effect due to the temporal coherence of electrons for the single quantum dot system.[25]For the parallel-coupled doublequantum-dot system,the current oscillation is similar to that of the single quantum dot,and different coupling strengths have different forms of oscillation.The present research is based on the perspective of dynamics.

The other aspect is regarding the Coulomb transition coupling between the quantum dots. In Ref. [4], we pointed out that different Coulomb coupling strengths between the sidecoupled double quantum dots can divide the singly occupied(SO)state of quantum dot 1 into three quasi-particle substates from the perspective of the spectral function. The spectral functions show different characteristics in different kondo regions. The effects of different coupling on different models were separately studied. Based on the work of Ref.[4],in this paper we further study the effects of the two coupling modes on the side-coupling double-quantum-dot system.

The structure of this article is organized as follows. In Section 2, the HEOM method is introduced and derived, and the common form of the time-dependent quantum transport current in a quantum-impurity system is given. In Section 3,firstly we investigate the influences of the different step voltageV,tunneling transition couplingt12temperatureT,e-e interactionU,and bandwidthWon the transport current within the side-coupled double-quantum-dot system. Secondly, we study the influence of the Coulomb interaction couplingU12on the transport current of the side-coupled double-quantumdot system in different Kondo regions. Section 4 provides the summary of the work.

2. Model and Hamiltonian

Based on the HEOM, we developed a set of nonperturbation methods for solving quantum impurities,[26-29]which can not only solve the quantum impurity problem in open systems,but also deal with the quantum dissipation problem in non-equilibrium.

As shown in Fig. 1, we study the side-coupled doublequantum-dot model with particle-hole symmetryε1↑=ε1↓=ε2↑=ε2↓=-U/2. QD1 and QD2 are identical,in which the two sides of QD1 are connected to the left and right leads respectively, and there may be tunneling transition couplingt12and Coulomb interaction couplingU12between QD2 and QD1. We take two quantum dots as research objects and describe their physical properties through the motion equation of the density matrix operator.The leads are regarded as the environment attached to the quantum dots,generally considered as a non-interacting Fermion bath. The influence of the environment on the quantum dots is described by the correlation function. By constructing a set of non-perturbative equations of motion about the reduced density matrix operator and the auxiliary density matrix operator,the dynamic transport current of the system is solved in the HEOM linear space. Under the Anderson impurity model,the total Hamiltonian of the quantumdot system,the leads and the interaction between them reads

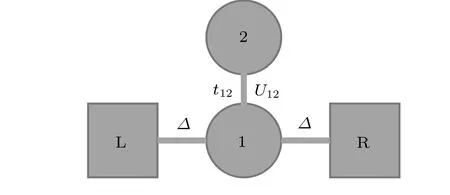
Fig.1. The model for side-coupled double-quantum-impurity systems.

The Hamiltonian coupling of the quantum-dot system and leads is

Let us start from the initial equilibrium steady state of the system:

When the voltage is applied to the leads, the system is out of balance and the current flowing from the left to the right lead isI(t). When the current reaches a steady state,we haveI(t)=IL(t)=-IR(t). The current value calculated in this paper refers to the current passing through the left leadIL(t).The electron occupancy numberN(t) of the quantum dots is expressed asN(t)=tr[a+iµaiµρ(t)]. The current flowing into the quantum dots through leadαis expressed as

where trSand trBrepresent the traces of quantum-dot system and lead, respectively;ρ+αµ=(ρ-αµ)†is the first-order auxiliary density operator obtained by solving the HEOM.

As a numerical method, the HEOM has the following characteristics. First of all, with the increase of truncation orderL, the calculation results of the corresponding physical quantities gradually converge in the full energy domain.In our calculations,if the error of the numerical results for each element of the density matrix or spectral function matrix ofL=NandL=N+1 is less than 5%,then we can consider the results to be convergent, since this will obtain sufficiently accurate values of the dynamic transport current. Secondly,the HEOM has great advantages in solving quantum-dot problems with high accuracy. In Ref.[25], the time-dependent dynamic current of single-level resonant tunneling obtained by the HEOM method is compared with the current obtained by the analytical formula based on Keldysh Green’s function, non-equilibrium Green’s function, time-dependent density matrix renormalization group and time-dependent numerical renormalization group,separately. It is found that the HEOM method can not only describe the dynamic behavior of the single-level system well, but also be superior to the latest time-based numerical renormalization group method in numerical solution.This also provides the premise for us to study the transport properties in the Kondo region of the side-coupled double-quantum-dot system.

3. Results and discussion

There may be two forms of interaction between the two quantum dots for the side-coupled double-quantum-impurity system. One is the tunneling type, which is represented by the transition coupling parametert12and is a necessary condition of the two-channel Kondo effect and the two-stage Kondo effect.[31-34]The second is the capacitive type, which is described by the Coulomb repulsion seen between the dots. It is expressed by the Coulomb interaction constantU12. This interaction is involved in single electron switches and other transport phenomena.[35,36]Since there appears to be no energy levels near the Fermi surface, the Kondo effect results in a large transport current and also the oscillating behavior of the current. The Hamiltonian of the side-coupled doublequantum-dot system is

The parameters are the same as mentioned above. For the tunneling type,γ=t12. For the capacitive type,the Hamiltonian is

Firstly, the capacitive coupling is ignored, and only the tunneling transition coupling is dealt with. Since the Kondo resonance assists the tunneling of electrons at low temperatures to produce a large resonant transport current,a new type of current oscillation appears.

The current transport characteristics of the side-coupled double-quantum-impurity system during different step voltages in the Kondo state are described in Fig. 2. The tunneling coupling between the two impurities as weak coupling was set at 0.1 meV. It could be seen that the current rapidly increases to its maximum value once the step voltage is applied, and further regular oscillations occur depending on the form of the step voltage applied. For example,when the voltageVL=-VR=0.3 mV, the maximum value of current is 10000 pA,and three apparent oscillations occur before reaching its stable value. WhenVL=-VR=0.1 mV,the maximum value of current is 5000 pA,and only one obvious oscillation occurs before reaching its stable value,and thus the amplitude is significantly reduced. This happens due to the time coherence corresponding to the step voltage as the electron tunnels through the quantum impurities. The accumulation and dissipation of the charges of the leads appearing on the left and right produce oscillatory behavior when the step voltage is changed suddenly. The larger the step voltage is, the faster the accumulation and dissipation of the charge would be,and the more obvious the oscillation behavior appears.In addition,all of the current values reach their respective stable values at 30 ps,irrespective of the voltage pulse form,corresponding to their respective steady-state current.This is because the longer relaxation time gives the tunneling electron enough time to respond to the bias change.

Fig. 2. The dynamic current of the side-coupled double-quantumimpurity system at different step voltages. The parameters adopted are t12 = 0.1 meV, kBT = 0.015 meV, Δ = 0.2 meV, W = 2 meV,U =2 meV,U12=0,ε1↑=ε1↓=ε2↑=ε2↓=-1 meV.

Figure 3 shows the oscillation form of the current in the side-coupled double-quantum-impurity system at differentt12and during large and small step voltages, respectively. It is found that,no matter how large a step voltage is added,the oscillation behaviors of the current fort12=0 andt12=0.1 meV are similar, whereas the amplitude of the current oscillation decreases and reaches a stable value faster when the coupling is weak. For example, whenVL=-VR=0.3 mV, the current of the system reaches a maximum value of 1.4 ps under the weak coupling condition oft12=0.1 meV and reaches the steady-state current value of 20 ps.However,whent12=0,the current reaches a maximum value of 1.8 ps, and there is still an oscillation behavior of small amplitude at 30 ps. This is because the ground state of the system maintains the Kondo singlet of each impurity when the tunneling transition coupling strengtht12is weak, and thus an oscillating behavior appears similarly to that of a single quantum dot. However,there will not only be an L-QD1-R for the current, but the L-QD1-QD2-QD1-R is also added to the system compared it to the single quantum dot, which would speed up the current transport. Ast12increases,the oscillation of the dynamic current changes significantly.When we compare the images oft12=0.1 meV andt12=0.2 meV under different step voltages,we find that no matter how large the step voltage is,when the system has weak coupling,the current would first reach a maximum value and then oscillate to a stable value,which is lower than the maximum value. However, whent12=0.2 meV is in the strong coupling,the maximum value of the current that appears first is the same as that of the steady-state value of the current that finally occurs after oscillation,or even slightly lower than the steady-state value itself. This is due to the fact that, whent12is small, the direct first-order coupling (t) is much stronger than the induced second-order antiferromagnetic spin coupling(J=4t2/U)present between the two impurities, in which the current oscillates like a single quantum impurity. Whent12is large, the spin-spin couplingJdominates, making the ground state of the system transform into the spin singlet of the two impurities, and thus the transport current shows different oscillatory behaviors.

Fig. 3. The dynamic current of the side-coupled double-quantumimpurity system at different step voltages and different transition coupling parameter t12. The parameters adopted are kBT =0.015 meV,Δ =0.2 meV, W =2 meV, U =2 meV, U12 =0, ε1↑=ε1↓=ε2↑=ε2↓=-1 meV.

In Fig. 4(a), we have shown a graph of current changing with time at different temperatures. According to the formula[37]

where ˜Δ=2Δ, the calculated Kondo temperature is approximatelykBTK≈0.122 meV. In the high-temperature region,such askBT ≈0.32 meV,only one maximum value appears in the picture of the dynamic current,and the current reaches the steady-state value soon after reaching this value. In the vicinity of the Kondo temperature,the current oscillates like that of in the high-temperature region. As the temperature begins to drop further,the current starts to oscillate in a new form. For example,atkBT=0.045 meV,slight oscillation occurs before reaching the steady-state current. The lower the temperature is, the larger the amplitude of the current oscillation is, and the more obvious the oscillation behavior would be, such as in the case ofkBT=0.015 meV. The steady-state values of current measured at 100 ps at different temperatures are given in Fig. 4(b). It can be seen that in the dynamic transport of the quantum-impurity system,the Kondo effect could be promoted by lowering the temperature to promote the oscillation of the dynamic current and to increase the steady-state current value.

Fig. 4. (a) The dynamic current of the side-coupled double-quantumimpurity system at different temperature T. (b)The steady-state values of current measured at 100 ps at different temperatures. The parameters adopted are VL =-VR =0.2 mV, t12 =0.1 meV, Δ =0.2 meV,W =2 meV,U =2 meV,U12=0,ε1↑=ε1↓=ε2↑=ε2↓=-1 meV.

Further,the effect of e-e interactionUon the current oscillation is studied.Figure 5 shows the results of the Kondo regionT ＜TKand the non-Kondo regionT ＞TK,respectively.The comparison between the two figures shows that the amplitude of the current oscillation decreases with the increase ofU, regardless of whether the current is present in the Kondo region or not, because the on-site e-e interaction induces the localization of the carrier. Taking a closer look at the Kondo region in Fig.5(a),it can be seen that the amplitude of the current oscillation decreases whenUincreases,but the frequency remains almost constant. The mechanism can be understood as follows. According to the analytical expression of the Kondo temperatureTK,TKincreases with the decrease ofU.Since the temperature is fixed (kBT=0.015 meV), a smallerUwould result in a larger difference betweenTandTK. Figure 4 indicates that the larger the difference is, the stronger the current oscillation would be. Therefore,for smallerU,the Kondo effect of the system would be enhanced,and the current would have a larger amplitude and a higher value of steadystate current. For example,the maximum amplitude of the oscillation increases from 6000 pA ofU=2.4 meV to 9000 pA ofU=1.8 meV, and the steady-state current value increases from 4000 pA ofU=2.4 meV to 6800 pA ofU=1.8 meV.

Fig. 5. The dynamic current of the side-coupled double-quantumimpurity system at different e-e interactions U.The parameters adopted are t12 =0.1 meV, VL =-VR =0.2 mV, Δ =0.2 meV, W =2 meV,U12 =0 , ε1↑=ε1↓=ε2↑=ε2↓=-1 meV. (a) In the Kondo regime,kBT =0.015 meV.(b)Out of the Kondo regime,kBT =0.32 meV.

Towards the end of this section,we also elucidate the effect of the bandwidthWof the lead on the current oscillation,which is difficult to treat using the nonequilibrium Green’s function method under the wideband approximation. The characteristics of the dynamic current corresponding to different bandwidths are shown in Fig.6. It can be seen that a largerWleads to a relatively larger amplitude of current oscillation and a relatively larger value of the steady-state current. This phenomenon mainly occurs due to the increase in the bandwidth, the accumulation, and consumption of the charge on both sides of the lead increases,resulting in the effect of current enhancement,that is,the bandwidth-enhanced lead capacitance contribution. In addition, we see that the frequency of oscillation is almost independent of the bandwidthW. Therefore,when studying the oscillation frequency behavior,we can roughly think that the electrode bandwidth has little influence on the current oscillation behavior.

It can be seen that for the side-coupled double-quantumimpurity systems, the frequency of current oscillation is related to the applied voltage,but not to the temperatureT,e-e interactionUand bandwidthW. It has been pointed out in Ref.[38]that in a single-quantum-impurity system, the magnitude of kondo oscillation frequency is equal to the magnitude of applied voltage. This conclusion is also confirmed by the calculation of the side-coupled double-quantum-impurity system. We find that the tunneling transitiont12also has an effect on the frequency of current oscillation: as the coupling strengtht12increases,the frequency also increases. This is because the system undergoes a continuous quantum phase transition from kondo singlet of the single quantum dot to spin singlet of the double quantum dots.

Fig. 6. The dynamic current of the side-coupled double-quantumimpurity system at different bandwidths. The parameters adopted are t12=0.1 meV,VL=-VR=0.2 mV,kBT =0.015 meV,Δ =0.2 meV,U =2 meV,U12=0,ε1↑=ε1↓=ε2↑=ε2↓=-1 meV.

We further ignore the tunneling coupling and study only the pure capacitive coupling.

As we can see from Fig.A1 in Appendix A,when there is no repulsive inter-dot Coulomb for QD1, there would be two Hubbard bands symmetrically distributed on both sides of the Fermi energy level,representing the singly occupied state below the Fermi energy level(SO state)and the double occupied state above the Fermi energy level (DO state), respectively.WhenU12is applied to the system, the SO state and the DO state splits into three quasi-particle states,SO0,SO1,SO2(the energy levels areε1,ε1+U12,ε1+2U12),and DO0,DO1,DO2(the energy levels areε1+U,ε1+U12+U,ε1+2U12+U),respectively. With the increase inU12,the SO0and DO0substates remain unchanged, while the SO1and DO1substates deviate from their original position at a rate of 1,and SO2and DO2substates deviate at a rate of 2.When combined with their initial positions, the SO2and SO1substates pass linearly and sequentially through the Fermi energy levels during this process.We find that within the parameter region of 0≤U12≤U,there exists an interesting interference phenomenon,as shown in the following figure.

The current steady-state values corresponding to differentU12in the side-coupled double-quantum-dot system are described in Fig.7.It can be seen that during 0≤U12≤0.2 meV,which is in the Kondo-I(K-I)region, the steady-state current value increases with the increase inU12. This is because the SO2first reaches the Fermi level and hence has an interference enhancement effect on the Kondo peak. When 0.2 meV＜U12＜1.2 meV,that is,the system is in the Kondo-Fano(K-F)region,the steady-state current presents an M-type with the increase ofU12. This is because in this region,with the increase inU12,the up-moving SO1and SO2state levels have impacts on the Kondo peak there.When 0.2 meV＜U12＜0.5meV,the SO2state first reaches the Fermi energy level and brings about the interference enhancement phenomenon of the K-F effect,which indicates that the steady-state current value increases with the increase inU12. After that,the SO1state also reaches the Fermi level and influences the Kondo peak together with the SO2state.The strengthening effect of the SO2state and the weakening effect of the SO1state would contradict each other,that is, the linear shape of 0.5 meV≤U12≤1.0 meV would become V-shaped. AsU12continues to increase, the energy level of the SO2state at 1.0 meV＜U12＜1.2 meV increases away from the Fermi level,and the SO1state occupies a dominant position, thus causing the interference suppression phenomenon of the K-F effect. When 1.2 meV≤U12≤2.0 meV,that is, in the Kondo-II (K-II) region, the steady-state current value decreases asU12increases.This is because the SO2state of the Hubbard sub-peak of interference Kondo peak is elevated and situated away from the Fermi level during this time,and only the SO1state has an impact on the system. By comparing the K-I region with the K-II region,it can be seen that only the SO2state and the SO1state possess different interference effects on the Kondo summit.

Fig. 7. The steady state value of current of side-coupled doublequantum-impurity systems at different Coulomb coupling constant U12.The parameters adopted are t12 = 0, VL = -VR = 0.3 mV, kBT =0.015 meV,Δ =0.2 meV,W =2 meV,U =2 meV,ε1↑=ε1↓=ε2↑=ε2↓=-1 meV.

Figure 8 shows the dynamic current transport images of the single quantum dot, K-I region, and the K-II region, respectively. It is seen that the dynamic transport current image within the K-I region (U12=0.1 meV) is roughly the same as that of the linear shape in the single quantum dot, and the dynamic transport current image in the K-II region is 1/3 the value of the single quantum dot at largeU12(U12=2 meV).This is because the coupling strength is weak,and the system behaves like a single quantum dot in the K-I region. However,in the K-II region,when the Coulomb coupling strength is very high,the SO2state is far away from the Fermi energy level, and the SO1state would have a major influence on the Kondo peak. The lines in this section are thus similar to those in the K-I region but consist of only a third of the value.

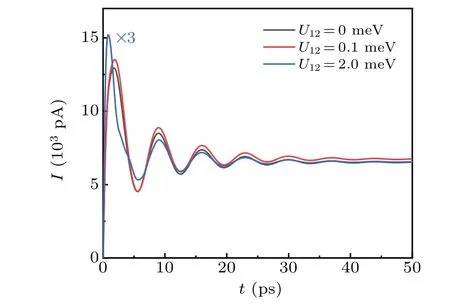
Fig.8. The current of side-coupled double-quantum-impurity systems at different Coulomb coupling constant U12. The parameters adopted are t12 =0, VL =-VR =0.3 mV, kBT =0.015 meV, Δ =0.2 meV,W =2 meV,U =2 meV,ε1↑=ε1↓=ε2↑=ε2↓=-1 meV.

4. Conclusion

In summary, we have studied time-dependent dynamic current transport properties of a side-coupled doublequantum-impurity system based on the HEOM method under different coupling conditions. The transport current would behave like a single quantum dot when the coupling strength is low during both tunneling and capacitive coupling.

Only for the tunneling transition in the Kondo region,the dynamic current oscillates due to the temporal coherence of the electron tunneling device. The oscillation frequency of the transport current is strongly dependent on the bias voltage applied by the lead and is insensitive to the change in values ofT,UandW.The amplitude of the current oscillation is in positive correlation with the electrode bandwidthWand in negative correlation with the e-e interactionU. With the increase of the couplingU12between impurities,the ground state of the system changes from a Kondo singlet of single impurity to a spin singlet in the numerical calculation,such that the system would experience three-parameter regions: the Kondo-I region,Kondo-Fano region and Kondo-II region with the change ofU12.When theU12value is very small,the current in the K-I region behaves like that in a single-quantum-impurity system,and only the SO2states would have a very weak interference enhancement effect on the Kondo peak. With the increase ofU12, two sub-summits present below the Fermi energy level are elevated and are passed through the Fermi level in turn.They produce fano interference on the Kondo peak, forming the K-F effect, which describes the phenomenon of interference enhancement,interference competition,and interference suppression. As theU12value continues to increase,the Hubbard sub-peak,which interferes with the Kondo peak,continues to elevate,such that it lies far away from the Fermi level.At this point, the transport current in the K-II region shows qualitative consistency with that in the K-I region, with a 1/3 quantitative relationship.

Our next work is to simultaneously change the tunneling transition couplingt12and the Coulomb interaction parameterU12to observe their effects on the dynamic transport current of the side-coupled double-quantum-impurity system.

Appendix A:Convergence of the HEOM method

When the HEOM method was used to solve the Andersen model of single impurity, in Ref. [29] we showed the spectral function of impurities under different truncation orders,and found that the results began to approach the accurate results when the truncation orderL=3. WhenLincreases to 4, the spectral function already overlaps with the results ofL=5. It can be verified that the calculation of HEOM converges rapidly with the increase of truncation orderLand satisfies the summation ruledωA(ω)=1 in numerical accuracy. For the side-coupled double-quantum-impurity system,it converges when the truncation orderL=3.

Fig. A1. Schematic diagram of Coulomb coupling configuration of side-coupled double-quantum-impurity systems.[4]

Fig.A2. Dynamic transport images of a side-coupled double-quantumimpurity system with different truncation orders L. The parameters adopted are t12 =0.1 meV, VL =-VR =0.3 mV, kBT =0.015 meV,Δ =0.2 meV,W =2 meV,U =2 meV,U12=0,pad´e=3,ε1↑=ε1↓=ε2↑=ε2↓=-1 meV.

As can be seen from Fig.A2, the current value ofL=3 is almost the same as that atL=4 andL=5, so the result atL=3 is accurate and is taken in this paper. An optimized spectral decomposition scheme,pad´e spectral decomposition,is adopted to consider all the information about the interaction of the electrode on the quantum dots as completely as possible.As can be seen from Fig.A3,the error range between pad´e=7 and pad´e=8 is less than 5%. The higher the pad´e number is,the higher the corresponding calculation cost is, so we take pad´e=7.

Fig.A3. Dynamic transport images of a side-coupled double-quantumimpurity system with the different values of pad´e. The parameters adopted are t12 =0.1 meV, VL =-VR =0.3 mV, kBT =0.015 meV,Δ =0.2 meV,W =2 meV,U =2 meV,U12 =0, L=3, ε1↑=ε1↓=ε2↑=ε2↓=-1 meV.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11774418 and 11374363).Computational resources were provided by the Physical Laboratory of High Performance Computing at Renmin University of China.