On the Onsager–Casimir reciprocal relations in a tilted Weyl semimetal

Bingyan Jiang(江丙炎) Jiaji Zhao(赵嘉佶) Lujunyu Wang(王陆君瑜) Ran Bi(毕然)Juewen Fan(范珏雯) Zhilin Li(李治林) and Xiaosong Wu(吴孝松)

1State Key Laboratory for Artificial Microstructure and Mesoscopic Physics,Frontiers Science Center for Nano-optoelectronics,Peking University,Beijing 100871,China

2Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

3Collaborative Innovation Center of Quantum Matter,Beijing 100871,China

Keywords: Onsager-Casimir relations,tilted Weyl semimetal,chirality-dependent Hall effect

Onsager’s reciprocity relations state that in thermodynamic systems out of equilibrium, the linear response coefficient,linking a thermodynamic driving force and the resultant flow,is a ic tensor. That is,Li j=Lji. In the presence of timereversal symmetry breaking fields, it becomes the Onsager-Casimir reciprocal relations,Li j(B)=Lji(-B),whereBdenotes all time-reversal symmetry breaking fields. These relations,rooted in the principle of microscopic reversibility,are a fundamental symmetry of nonequilibrium statistical systems.When multiple coupled pairs of flows and thermodynamic forces are involved, the relations can offer insights into the connection between different response coefficients that seem,at first glance, unrelated. For instance, in his seminal papers in 1931, Onsager derived the relations for several coupled irreversible processes and related different coefficients to one another.[1,2]The reciprocal relations have also played an important role on understanding various spin-related transport.[3]

Recently, an unusual chirality-dependent Hall effect and magnetoresistance that are antisymmetric in both magnetic field and magnetization were predicted to occur in tilted topological Weyl semimetals.[4-10]It was suggested that such an antisymmetry violates the Onsager-Casimir reciprocal relations.[8]Soon, the antisymmetric Hall and magnetoresistance were experimentally observed in a magnetic Weyl semimetal,Co3Sn2S2.[11]The phenomenon is originated from the Berry curvature of energy bands and involves several effects. In particular, the longitudinal linear magnetoresistance results from the Berry curvature correction to the phase space volume, while the Hall effect consists of contributions from the chiral chemical potential and the anomalous velocity. Here, we study the chirality-dependent Hall effect in Co3Sn2S2,with a focus on the validity of the Onsager-Casimir reciprocal relations. Two methods were employed and it was found that the reciprocal relations hold for this Hall effect.The relations connect the effect of the chiral chemical potential to that of the anomalous velocity. Despite only one pair of flow and force at work,our results reveal an intriguing connection between two effects,which deepens our understanding of Berry-curvature-related electrical transport.

Co3Sn2S2single crystals were grown by the chemical vapor transport method[11]and polished to a bar shape for the transport measurements. We utilized silver paste to fabricate the electrical contacts. Before applying the paste, the crystal was treated with Ar plasma to improve the contact.The device is shown in the inset of Fig.1(a)and thexaxis in the diagram is along the crystal [100] direction. The electrical transport measurements were performed using a low frequency lock-in method. A typical current of 2 mA-3 mA was employed. The angular dependence experiment was carried out using a motorized rotator stage with a resolution of 0.02°. Our samples exhibit transport properties similar to previous reports.[11-14]The temperature dependence of the longitudinal resistivityρyyis shown in Fig. 1(a), where a ferromagnetic phase transition manifests as a clear kink at the Curie temperatureTc～175 K.BelowTc, the anomalous Hall effect is observed, as shown in Fig. 1(b). The Hall resistivityρxyjumps at the coercive fieldBcand shows a linear dependence on the magnetic field aboveBc, from which we obtain an ordinary Hall coefficientRH=0.51 µΩ·cm/T and a corresponding carrier density of 1.2×1021cm-3.

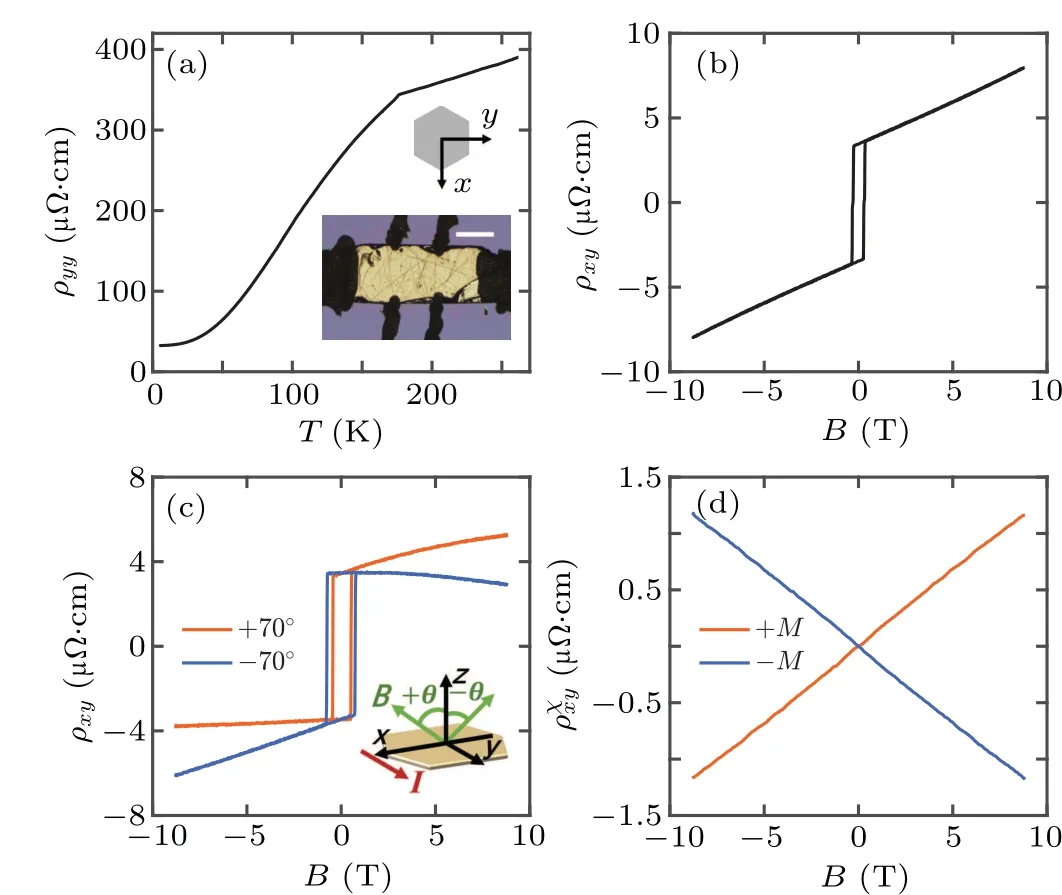
Fig.1. Basic transport properties of Co3Sn2S2 sample#1 and the chiralitydependent Hall effect. (a) Temperature dependence of the longitudinal resistivity ρyy. A clear kink indicates a Curie temperature of 175 K.The inset shows the Hall bar device and the scale bar is 300µm. (b)Anomalous Hall effect at T =50 K.The linear dependence of ρxy on the magnetic field above Bc suggests a single carrier type. (c) Hall resistivity as the magnetic field scans along ±70° in the xz plane at T =50 K. The inset depicts the measurement setup and the magnetic field direction.(d)The chirality-dependent Hall resistivity ρχxy obtained by symmetrizing the data in panel(c).ρχxy is linear in magnetic field and changes its sign as the magnetization reverses.

The chirality-dependent Hall effect satisfiesρxy(B,M)=ρxy(-B,-M), which is consistent with the Onsager-Casimir reciprocal relations.[11]However, to prove that the reciprocal relations hold,one needs to verifyρxy(B,M)=ρyx(-B,-M).One method is to attest the reciprocity theorem

Fig. 2. Verification of the reciprocal theorem, Eq. (1). (a) R12,34(B) and R34,12(-B)at different angles in the xz plane for T =50 K.Data are shifted for clarity. (b)-(c)(B)and(-B)at 80° by data antisymmetrizing, respectively. The bottom inset depicts the measurement configuration,while the top inset shows the angle definition.

However, equation (1) is a global symmetry. In principle, a whole series of four-probe measurements must be carried out and all results must comply with Eq. (1) in order to prove the validity of the Onsager-Casimir relations.[32,33]We now attempt another method,i.e.,direct verification of the local symmetry ofρxy(B,M)=ρyx(-B,-M). Note that there is a practical disadvantage in this method, as it is difficult to prepare Hall bars along two directions on the same crystal.In Fig.2,R12,34(B,M),corresponding toρxy(B,M),was measured. We had to prepare a Hall bar with another sample to measureρyx(-B,-M). Since no two samples can have exactly the same resistivity,only a semi-quantitative comparison will be made.

Fig. 3. Angular dependence of the Hall resistance. (a)-(b) Angular dependence of R12,34(B) and R34,12(-B) at B=8.8 T for T =50 K. (c)-(d)Angular dependence of(B)and(-B)by data antisymmetrizing.The same angular dependence of R and Rχ under two configurations further verifies the reciprocal theorem.

Fig. 4. Verification of the local Onsager-Casimir relations. (a) ρyx(-B)of sample #2 at several angles for T =50 K. The behavior is similar to sample #1. Data are shifted for clarity. (b) ρχyx(-B) at 80° for positive and negative magnetization. The top inset depicts the measurement setup.The bottom inset shows an optical image of sample#2 and the scale bar is 300µm.

Figure 4(a) displays the measuredρyx(-B) atθ=80°,0°,-80°for sample #2. AboveBc,ρyxexhibits a linearBdependence,from which a carrier density of 8.4×1020cm-3is obtained. It is slightly smaller than the carrier density of sample #1. The resistivity at zero field is about 125 µΩ·cm,compared to 65 µΩ·cm of sample #1. With increasing magnetic field or angleθ,ρyx(-B) at±θdiverge. This behavior qualitatively agrees with that observed in sample#1. The chirality-dependent Hall resistivityρχyx(-B) can be extracted by symmetrizing,depicted in Fig.4(b). It is antisymmetric in both magnetic field and magnetization,mimickingρxy(B,M),which confirms the local Onsager-Casimir reciprocal relations. The amplitude ofρχyxfor sample #2 is nearly twice as much as that for sample#1,which we believe can be attributed to the difference of a factor of 2 in the resistivity.

To reveal the implication of the reciprocal relations on the chirality-dependent Hall effect,it is necessary to identify various effects of the Berry curvature involved in the phenomenon.Start from the equations of motion for band electrons. The velocity can be expressed as

When calculating the integral, it should be born in mind that Weyl cones appear in pairs. There are three contributions that are linear in magnetic field and electric field, which are nonzero only when Weyl cones are tilted. One is the product of the first term of Eq.(2)and the second term in Eq.(3). It generally contributes to the diagonal current and hence is not of our interest. We write down the other two contributions as

The first current is the contribution of the anomalous velocity from the shifted distribution, denoted asjA. The second current is the contribution of the velocity from the chiral chemical potential,denoted asjC.

Fig. 5. Schematic diagram of different contributions to the B-linear transverse current. (a) Weyl cones of χ =±1 tilt along the y direction.The Fermi level tilts due to the electric field. (b) Anomalous velocity va ∝(vk·Ωk)·B (red arrows) and the distribution function shift ΔfE ∝vk·E (contour plot)due to E field,where E‖y and B‖x. (c)B-linear current due to vaΔ fE (blue arrows on the Fermi surface),the integration of which over Fermi surfaces yields jA. (d)The influence of the chiral chemical potential on the Fermi level. The Fermi level also tilts as vk·Ωk varies on the Fermi surface. (e)vk (red arrows)and the influence of the chiral chemical potential on the distribution function Δfca ∝(B·E)(vk·Ωk)(contour plot)on the Fermi surface,where E‖-x and B‖x. (f)B-linear current due to vkΔ fca (blue arrows).

Our experiments indicate that the Onsager-Casimir reciprocal relations hold for the chirality-dependent Hall effect,ρxy(B,M)=ρyx(-B,-M). Based on the above analysis on the origin ofρxyandρyx, it can be therefore concluded thatjA(B,M) =jC(-B,-M) in our experiment configurations.Although these two currents are manifests of different effects,our results suggest that they are intricately connected.

Having verified the reciprocal relations under a particular electric and magnetic field configuration and pointed out its implication,we generalize the conclusion to all configurations. Substituting Eqs.(2)and(3)into Eq. (4)and dropping the term for the anomalous Hall effect, one can express the conductivity tensor as

wherevidenotes thei-th component ofvk. It was incorrectly concluded that equation (6) violates the reciprocal relations.[8]This misunderstanding stems from the implicit dependence of the anomalous velocity on the magnetization.In a time-reversal-symmetry-broken Weyl semimetal, reversing the magnetization leads to a reversal of the chiralities of Weyl nodes.[36]Thus, the sign ofΩkdepends on the sign of the magnetization. Taking the magnetization into consideration, equation (6) indeed satisfies the Onsager-Casimir reciprocal relations,σi j(B,M)=σji(-B,-M). WhenΩ=0,equation (6) is reduced to the conventional formula. The effect of the Berry curvature is to introduce a correction (the anomalous velocity)to the velocity,besides the change of the phase space volume.

Acknowledgements

We are grateful for discussions with J. Feng, J. R. Shi and H. Z. Lu. Project supported by the National Key Basic Research Program of China(Grant No.2020YFA0308800)and the National Natural Science Foundation of China(Grant Nos. 11774009 and 12074009), the Natural Science Foundation of Beijing(Grant No.Z200008),and the Youth Innovation Promotion Association of the Chinese Academy of Sciences(Grant No.2021008).