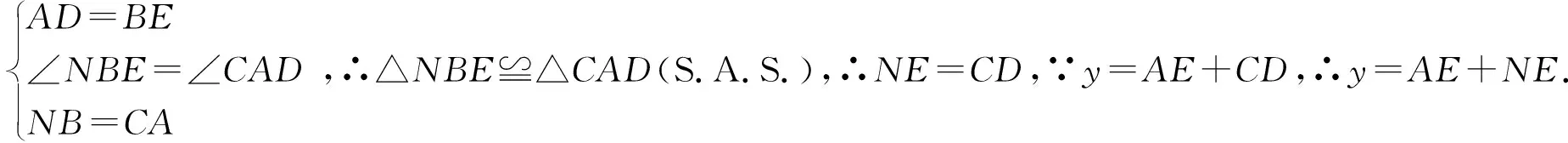“两图”相辉映 “四招”定乾坤
215616 江苏省张家港市妙桥中学 陈 冬
中考数学卷里常常会出现这样一类题,几何图形和函数图形同时出现在一道题里,相得益彰.笔者撷取此类以选择题或填空题形式出现的题,具体剖析其难点、关键点及破解方法.
一、 由几何图形的特征来确定函数图像的特性
例1(2021内蒙古通辽中考) 如图1,在矩形ABCD中,AB=4,BC=3,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,联结PQ.设点P的运动路程为x,PQ2为y,则y关于x的函数图像大致是( )
评析:本例考查了由两动点所引发的PQ2的不同计算方式,由此得出PQ2即y随x变化的不同函数关系式,于是可画出不同的函数图像.解这道题的关键是牢牢抓住点P只可能在矩形ABCD的两条边AB,BC上运动,点Q只可能在矩形ABCD的两条边AD,DC上运动.由于矩形ABCD中AB=DC=4,AD=BC=3,而动点P,Q都同时从点A出发,点P的运动路径为A→B→C,点Q的运动路径为A→D→C,又点P,Q的运动速度相同.为此,必须从三个角度来分析出点P,Q的准确位置,即0≤x≤3时,如图1,点P在边AB上,点Q在边AD上;3≤x≤4时,如图2,点P在边AB上,点Q在边DC上;4≤x≤7时,如图3,点P在边BC上,点Q在边DC上.由此根据勾股定理分别计算出PQ2即y关于x的函数表达式,然后根据函数表达式判断出相应的图像.

图2图3
解答:在Rt△APQ中,∠QAP=90°.当0≤x≤3时,AP=AQ=x(如图1所示),由勾股定理可得y=PQ2=AP2+AQ2=x2+x2=2x2;当3≤x≤4时,DQ=x-3,AP=x(如图2所示),过点Q作QE⊥AB于E,则AE=DQ=x-3,QE=EP=3,由勾股定理可得y=PQ2=QE2+EP2=32+32=18;当4≤x≤7时,CP=7-x,CQ=7-x(如图3所示),由勾股定理可得y=PQ2=CP2+CQ2=(7-x)2+(7-x)2=49-14x+x2+49-14x+x2=2x2-28x+98.
综上可知,0≤x≤3时,此函数为二次函数且开口向上;3≤x≤4时,此函数为常数函数;4≤x≤7时,此函数为二次函数且开口向上.所以本题应选C.
例2(2021山东聊城中考) 如图4,四边形ABCD中,已知AB∥CD,AB与CD之间的距离为4,AD=5,CD=3,∠ABC=45°,点P,Q同时由A点出发,分别沿边AB,折线ADCB向终点B方向移动,在移动过程中始终保持PQ⊥AB,已知点P的移动速度为每秒1个单位长度,设点P的移动时间为x秒,△APQ的面积为y,则能反映y与x之间函数关系的图像是( )
评析:本例同样考查了由两动点所引发的△APQ面积的不同计算方式,由此得出△APQ的面积y随x变化的不同函数关系式,依据不同函数关系式可画出不同的函数图像.从本例来看,解决问题的关键还是要牢牢抓住点P只在梯形ABCD的边AB上运动,点Q则可能在梯形ABCD的三条边AD,DC,CB上运动.为此,可依据点Q可能出现的位置分别从三个角度求△APQ的面积,于是便得出△APQ的面积y关于x的函数表达式,然后根据函数表达式即可判断出相应的图像.


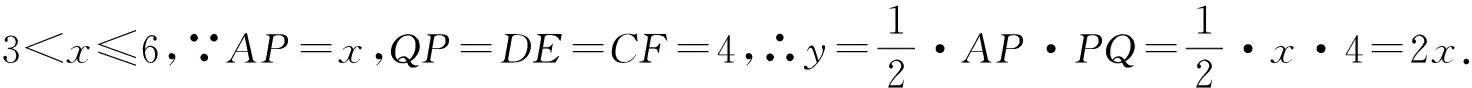
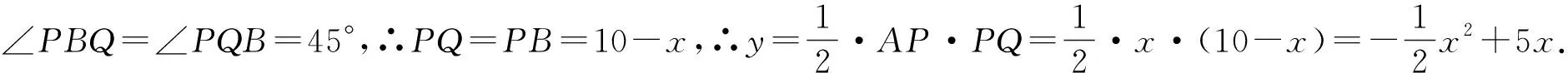
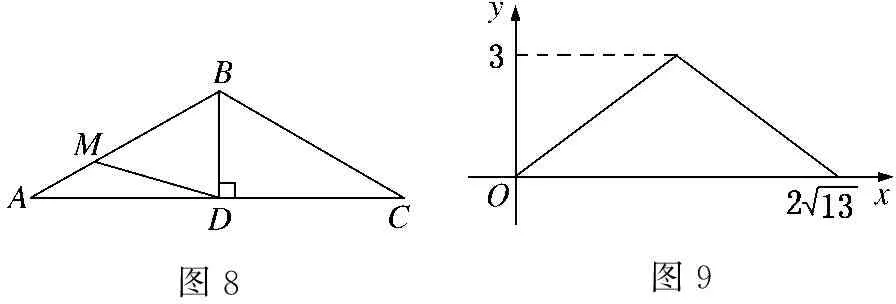
综上可知,0≤x≤3时,此函数为二次函数且开口向上;3 图6图7 招式1:两道例题均为动点问题,涉及的几何图形一般为圆、四边形(如正方形、矩形、菱形、平行四边形、梯形等)、三角形(等边三角形、等腰三角形、等腰直角三角形等),动点往往沿着这些几何图形的边、对角线或某一条线运动,问题的关键在于动点可能会出现在多个位置上.因此,必须学会采用分类讨论思想,对于动点可能出现的所有情况画出相应的几何图形,找出对应的取值范围,利用几何图形的性质计算出不同的函数关系式,这样就可以自然地画出不同函数关系式所对应的函数图像了. 例3(2021甘肃定西中考) 如图8,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从A点出发,沿折线AB→BC方向运动,运动到点C停止.设点M的运动路程为x,△AMD的面积为y,y与x的函数图像如图9所示,则AC的长为( ) A.3 B.6 C.8 D.9 图8图9 ①+2×2得AD2+BD2+2AD×BD=13+2×6=25,∴(AD+BD)2=25,∴AD+BD=5(负值舍去) ③. ①-2×2得AD2+BD2-2AD×BD=13-2×6=1,∴(AD-BD)2=1,∴AD-BD=1(AD>BD,负值舍去) ④. ③+④解得AD=3,∴AC=2AD=6.因此,本题正确答案应为B. 例4(2021河南中考) 如图10,矩形ABCD中,点E为BC的中点,点P沿BC从点B运动到点C,设B,P两点间的距离为x,PA-PE=y,图11是点P运动时y随x变化的关系图像,则BC的长为( ) 图10图11 A.4 B.5 C.6 D.7 评析:从本例中的图11来看,第一个关键点是当x=0时,y=1,其实结合图10来看,就是动点P在点B位置,此时PA-PE=y,即为BA-BE=1 ①.再看图11中的第二个关键点,图像显示是最高点,即此时PA-PE=y取得最大值为5,结合图10及三角形三边关系知,只有当动点P与中点E重合时,即PA-PE=AE=y=5.根据已知矩形ABCD易知∠B=90°,由勾股定理得AB2+BE2=AE2=25 ②.将①②联立成一个二元二次方程组,解这个方程组可求出BE的值,由点E为BC的中点知BC=2BE,即可得出BC的长度. 解答:由图10和图11知当x=0时,即点P在点B的位置,BA-BE=1 ①. 在△PAE中,有PA-PE 由①得BA=BE+1 ③. 将③代入②得(BE+1)2+BE2=25,即BE2+BE-12=0,(BE+4)(BE-3)=0,BE+4=0或BE-3=0,BE=-4(舍去)或BE=3.∵点E为BC的中点,∴BC=2BE=2×3=6. 因此,本题正确答案应为C. 招式2:两例均有一幅几何图形(三角形、四边形等)和一幅由几何图形上点的运动而绘制出的函数图像.函数图像一般简单明了,但面对并不复杂的函数图像,学生往往不知所云,无从着手,问题的关键在于函数图像上的点和数据预示着什么.因此,必须学会读懂关键点和数据,将关键数据“放入”几何图形中去,利用某些几何图形(等腰三角形、直角三角形、等腰梯形、矩形、菱形、正方形等)的性质研究和计算出边、角间存在的某些关系,有时再借助方程、方程组等可以更顺利地解决此类问题. 例5(2021广西玉林中考) 如图12,在Rt△ABC中,∠A=90°,点P从点A出发,沿三角形的边以1厘米/秒的速度逆时针运动一周,如图13所示是点P运动时,线段AP的长度y(cm)随运动时间x(秒)变化的关系图像,则图13中点P的坐标是( ) 图12图13 A.(13,4.5) B.(13,4.8) C.(13,5) D.(13,5.5) 评析:观察图13的函数图像,可以发现其由三段组成.根据题意“点P从点A出发,沿三角形的边逆时针运动一周”知,点P的运动路径为A→B→C→A,即点P分别在线段AB,BC,CA上运动.将两图结合起来看,图13中的三段恰好对应图12中的三条线段AB,BC,AC,于是由题意和图13可得AB=8,BC=10.与此同时,从图13中点P的横坐标为13可知,点P正好为线段BC的中点,根据“直角三角形斜边上的中线等于斜边的一半”,可求得此时线段AP的长度,即y的值,则图13中点P的坐标便可求得. 例6(2021山东菏泽中考) 如图14,在平面直角坐标系中,矩形ABCD在第一象限,且BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形ABCD截得的线段长为a,直线在x轴上平移的距离为b,a,b间的函数关系图像如图15所示,那么矩形ABCD的面积为( ) 招式3:这两道例题风格稍有不同,但有共同之处,其综合性均较强.尤其是例6对学生而言更具挑战性,如何画出与函数图像相对应的图形,是解决此类问题的关键所在和难点.因此,必须学会把握问题的整体与局部,看清几何图形中动点运动的整个路径和某些特殊位置,读懂函数图像所描述的动点运动轨迹及每个数据的真实内涵,真正理解几何图形和函数图像的相得益彰、相互阐述,用全面、准确的辩证唯物主义观点来思考问题、研究问题、解决问题. 例7(2021湖南衡阳中考) 如图17,菱形ABCD的对角线AC与BD相交于点O,P,Q两点同时从O点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P的运动路线为O-A-D-O,点Q的运动路线为O-C-B-O.设运动的时间为x秒,P、Q间的距离为y厘米,y与x的函数关系的图像大致如图18所示,当点P在A-D段上运动且P、Q两点间的距离最短时,P、Q两点的运动路程之和为________厘米. 解答:由图17和图18可知,当点P从O向A运动时,点Q从O向C运动时,y的值不断增大. 如图19,过点O作OF⊥BC于F,反向延长OF交AD于E,此时易得OE⊥AD. 当点P在A-D段上运动,点P运动到点E处,点Q在C-B段上运动,点Q运动到点F处时,P、Q两点的距离最短. 例8(2021湖北武汉中考) 如图20,在△ABC中,AB=AC,∠BAC=90°,边AB上的点D从顶点A出发,向顶点B运动,同时,边BC上的点E从顶点B出发,向顶点C运动,D,E两点运动速度的大小相等,设x=AD,y=AE+CD,y关于x的函数图像如图21所示,图像过点(0,2),则图像最低点的横坐标是________. 评析:观察如图21所示的函数图像,根据题意y=AE+CD及图像经过点(0,2),可知y=AB+AC=2,由AB=AC即可得出AB=AC=1.因为D,E两点运动速度的大小相等,可以通过构造△NBE≌△CAD(如图22所示)将线段CD移到线段NE处,则y=AE+CD变成y=AE+NE,由题意“图像最低点”,即y取得最小值知,只有A,E,N三点共线,然后可以利用构造△NBE∽△AFE(如图22所示),求出图像最低点的横坐标x的值. 招式4:这两道例题以双动点为载体,嵌入“最值”,使问题的难度陡增,是典型的填空式压轴题.从这两例的解答来看,主要还是利用特殊四边形(如菱形等)、全等三角形和相似三角形等的性质,但问题的关键是如何找出这个“最值”.遇到这种情况,需要对“最值”作一梳理,线段的最值问题主要有定点到定点(联结线段,理由是两点之间线段最短),定点到定线(作垂线段,理由是垂线段最短).解决这类几何最值问题的主要方法是转化,通过分析变化过程中的不变特征,利用几何变换、图形性质等手段对所求量进行转化,构造出符合几何最值问题理论依据的基本结构,进而解决问题.
二、 由函数图像的特征来确定几何图形的特性
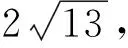



三、 两图相得益彰,“全局”来把控




四、 两图不离不弃,“最值”细思量