数论函数方程tφ2(n(n+1))=S(SL(n17))的可解性
周建华,瞿云云,朱山山,黄华伟
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
0 引言
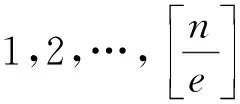
1 主要引理
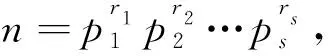
引理2[4]当n≥2时,有φ(n) 引理4[4]对于素数p和正整数k,有S(pk)≤kp;特别地,当k 引理6[6]对任意的正整数m和n,有 特别地,当gcd(m,n)=1时,有 φ(mn)=φ(m)φ(n)。 定理方程 tφ2(n(n+1))=S(SL(n17)) (1) 有正整数解,且正整数解为(t,n)=(1,1),(1,27),(6,6),(6,9),(9,4),(18,3),(20,2)。 (2) S(SL(n17))=S(p17r)≤17rp (3) 其中p是n的素因子,且r是p在n的标准分解式中的指数。由引理3、引理6和(1)知 (4) 由引理5和(3)知 (5) 所以有1≤t≤68rp,3≤n≤68rp。从而由(5)知 (6) 其中n=prm,gcd(p,m)=1,所以有 2r-2≤pr-2(p-1)≤pr-2(p-1)φ(m)≤34r (7) 即 2r-2≤34r (8) 对(8)两端取对数有 (r-2)log 2≤log 34+logr (9) 由(9)解得r≤10。以下对r和p的不同取值, 分10种情况讨论: 情况1 若r=1,由(7)知p(1-2)(p-1)≤34,故p≥2。 当p=2时,有1≤t≤136,3≤n≤136,所以由(3)、(4)有tφ(n(n+1))=2S(217)=2×20=40,经计算得到(t,n)=(1,10),(1,11),(5,4),(5,5),(10,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(1,10),(1,11),(5,4),(5,5),(10,3)都不是方程(1)的正整数解。 当p=3时,有1≤t≤204,3≤n≤204,所以有tφ(n(n+1))=2S(317)=2×36=72,经计算得到(t,n)=(1,13),(3,7),(3,8),(3,9),(6,6),(9,4),(9,5), (18,3)。将(t,n)的值代入方程(1)检验知,(t,n)= (6,6),(9,4),(18,3)是方程(1)的正整数解。 当p=5时,有1≤t≤340,3≤n≤340,所以有tφ(n(n+1))=2S(517)=2×75=150,经计算得到,此时方程(1)无正整数解。 当p=7时,有1≤t≤476,3≤n≤476,所以有tφ(n(n+1))=2S(717)=2×105=210,经计算得到,此时方程(1)无正整数解。 当p=11时,有1≤t≤748,3≤n≤748,所以有tφ(n(n+1))=2S(1117)=2×176=352,经计算得到(t,n)=(2,23),(44,4),(44,5),(88,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(2,23),(44,4),(44,5),(88,3)都不是方程(1)的正整数解。 当p=13时,有1≤t≤884,3≤n≤884,所以有tφ(n(n+1))=2S(1317)=2×208=416,经计算得到(t,n)=(52,4),(52,5),(104,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(52,4),(52,5),(104,3)都不是方程(1)的正整数解。 当p=17时,有1≤t≤1 156,3≤n≤1 156,所以有tφ(n(n+1))=2S(1717)=2×289=578,经计算得到,此时方程(1)无正整数解。 当p≥19时,有1≤t≤68p,3≤n≤68p,由引理4,有tφ(n(n+1))=2S(p17)=34p,由于n=pm且gcd(p,m)=1,所以有(p-1)|34,从而(p-1)≤34,即p≤35,但19≤p≤35的素数都不满足(p-1)|34,所以当p≥19时,方程(1)无正整数解。 情况2 若r=2,由(7)知p(2-2)(p-1)≤34×2,故p≤69。 当p=2时,有1≤t≤272,3≤n≤272,所以有tφ(n(n+1))=2S(217×2)=2×36=72,经计算得到(t,n)=(1,13),(3,7),(3,8),(3,9),(6,6),(9,4),(9,5),(18,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(6,6),(9,4),(18,3)是方程(1)的正整数解。 当p=3时,有1≤t≤408,3≤n≤408,所以有tφ(n(n+1))=2S(317×2)=2×72=144,经计算得到(t,n)=(1,19),(2,13),(3,12),(3,14),(6,7),(6,8),(6,9),(12,6),(18,4),(18,5),(36,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(6,9)是方程(1)的正整数解。 当p=5时,有1≤t≤680,3≤n≤680,所以有tφ(n(n+1))=2S(517×2)=2×140=280,经计算得到(t,n)=(7,10),(7,11),(35,4),(35,5),(70,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(7,10),(7,11),(35,4),(35,5),(70,3)都不是方程(1)的正整数解。 当p=7时,有1≤t≤952,3≤n≤952,所以有tφ(n(n+1))=2S(717×2)=2×210=420,经计算得到(t,n)=(35,6),(105,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(35,6),(105,3)都不是方程(1)的正整数解。 当p=11时,有1≤t≤1 496,3≤n≤1 496,所以有tφ(n(n+1))=2S(1117×2)=2×352=704,经计算得到(t,n)=(4,23),(11,15),(88,4),(88,5),(176,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(4,23),(11,15),(88,4),(88,5),(176,3)都不是方程(1)的正整数解。 当p=13时,有1≤t≤1 768,3≤n≤1 768,所以有tφ(n(n+1))=2S(1317×2)=2×416=832,经计算得到(t,n)=(13,15),(104,4),(104,5),(208,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(13,15),(104,4),(104,5),(208,3)都不是方程(1)的正整数解。 当p=17,19,23,29,31时,经计算得到,此时方程(1)都无正整数解。 当p≥37时,有1≤t≤136p,3≤n≤136p,由引理4,有tφ(n(n+1))=2S(p17×2)=68p,由于n=p2m且gcd(p,m)=1,所以有(p-1)|68,从而(p-1)≤68,即p≤69,但37≤p≤69的素数都不满足(p-1)|68,所以当p≥37时,方程(1)无正整数解。 情况3 若r=3,由(7)知p(3-2)(p-1)≤34×3,故p≤10,即p=2,3,5,7。 当p=2时,有1≤t≤408,3≤n≤408,所以有tφ(n(n+1))=2S(217×3)=2×56=112,经计算得到(t,n)=(14,4),(14,5),(28,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(14,4),(14,5),(28,3)都不是方程(1)的正整数解。 当p=3时,有1≤t≤612,3≤n≤612,所以有tφ(n(n+1))=2S(317×3)=2×108=216,经计算得到(t,n)=(1,26),(1,27),(2,18),(3,13),(9,7),(9,8),(9,9),(18,6),(27,4),(27,5),(54,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(1,27)是方程(1)的正整数解。 当p=5时,有1≤t≤1 020,3≤n≤1 020,所以有tφ(n(n+1))=2S(517×3)=2×210=420,经计算得到(t,n)=(35,6),(105,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(35,6),(105,3)都不是方程(1)的正整数解。 当p=7时,有1≤t≤1 428,3≤n≤1 428,所以有tφ(n(n+1))=2S(717×3)=2×315=630,经计算得到,此时方程(1)无正整数解。 情况4 若r=4,由(7)知p(4-2)(p-1)≤34×4,故p≤5,即p=2,3,5。 当p=2时,有1≤t≤544,3≤n≤544,所以有tφ(n(n+1))=2S(217×4)=2×72=144,经计算得到(t,n)=(1,19),(2,13),(3,12),(3,14),(6,7),(6,8),(6,9),(12,6),(18,4),(18,5),(36,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(6,9)是方程(1)的正整数解。 当p=3时,有1≤t≤816,3≤n≤816,所以有tφ(n(n+1))=2S(317×4)=2×141=282,经计算得到,此时方程(1)无正整数解。 当p=5时,有1≤t≤1 360,3≤n≤1 360,所以有tφ(n(n+1))=2S(517×4)=2×275=550,经计算得到,此时方程(1)无正整数解。 情况5 若r=5,由(7)知p(5-2)(p-1)≤34×5,故p≤3,即p=2,3。 当p=2时,有1≤t≤680,3≤n≤680,所以有tφ(n(n+1))=2S(217×5)=2×88=176,经计算得到(t,n)=(1,23),(22,4),(22,5),(44,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(1,23),(22,4),(22,5),(44,3)都不是方程(1)的正整数解。 当p=3时,有1≤t≤1 020,3≤n≤1 020,所以有tφ(n(n+1))=2S(317×5)=2×174=348,经计算得到(t,n)=(29,6),(87,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(29,6),(87,3)都不是方程(1)的正整数解。 情况6 若r=6,由(7)知p(6-2)(p-1)≤34×6,故p≤3,即p=2,3。 当p=2时,有1≤t≤816,3≤n≤816,所以有tφ(n(n+1))=2S(217×6)=2×106=212,经计算得到(t,n)=(53,3)。 将(t,n)的值代入方程(1)检验知,(t,n)=(53,3)不是方程(1)的正整数解。 当p=3时,有1≤t≤1 224,3≤n≤1 224,所以有tφ(n(n+1))=2S(317×6)=2×210=420,经计算得到(t,n)=(35,6),(105,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(35,6),(105,3)都不是方程(1)的正整数解。 情况7 若r=7,由(7)知p(7-2)(p-1)≤34×7,故p≤2,即p=2。 当p=2时,有1≤t≤952,3≤n≤952,所以有tφ(n(n+1))=2S(217×7)=2×124=248,经计算得到(t,n)=(31,4),(31,5),(62,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(31,4),(31,5),(62,3)都不是方程(1)的正整数解。 情况8 若r=8,由(7)知p(8-2)(p-1)≤34×8,故p≤2,即p=2。 当p=2时,有1≤t≤1 088,3≤n≤1 088,所以有tφ(n(n+1))=2S(217×8)=2×140=280,经计算得到(t,n)=(7,10),(7,11),(35,4),(35,5),(70,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(7,10),(7,11),(35,4),(35,5),(70,3)都不是方程(1)的正整数解。 情况9 若r=9,由(7)知p(9-2)(p-1)≤34×9,故p≤2,即p=2。 当p=2时,有1≤t≤1 224,3≤n≤1 224,所以有tφ(n(n+1))=2S(217×9)=2×158=316,经计算得到(t,n)=(79,3)。将(t,n)的值代入方程(1)检验知,(t,n)=(79,3)不是方程(1)的正整数解。 情况10 若r=10,由(7)知p(10-2)(p-1)≤34×10,故p≤2,即p=2。 当p=2时,有1≤t≤1360,3≤n≤1360,所以有tφ(n(n+1))=2S(217×10)=2×176=352,经计算得到(t,n)=(2,23),(44,4),(44,5),(88,3)。 将(t,n)的值代入方程(1)检验知,(t,n)=(2,23),(44,4),(44,5),(88,3)都不是方程(1)的正整数解。 综上可知, 方程(1)的所有正整数解的情况如定理的证明所示。 本文讨论了形如tφ2(n(n+1))=S(SL(nk))的数论函数方程的一个具体的数论函数方程tφ2(n(n+1))=S(SL(n17))的正整数解,得到了该方程有7组正整数解。对于形如tφ2(n(n+1))=S(SL(nk))的数论函数方程,当k为某一正整数时,其所确定的数论函数方程也可采用本文的研究方法进行求解。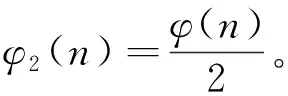
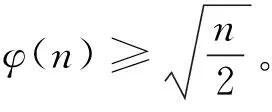
2 定理及其证明
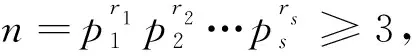
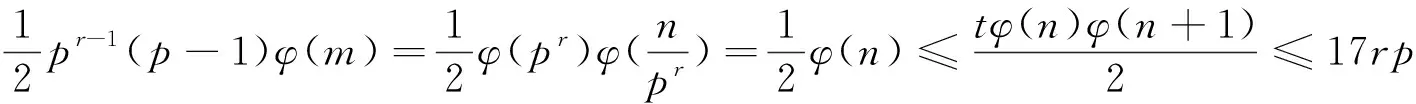
3 结语

