一种适用于大幅值Quasi周期轨道的数值构造方法

李瑞龙，朱战霞

(西北工业大学航天学院，西安 710072)

0 引 言

近年来，各航天大国都在加速布局地月空间开发与深空探测[1-2]，平动点任务是其中的重要组成部分，各航天大国均制定了未来数年的平动点任务规划。平动点及周期轨道是圆型限制性三体问题(CRTBP)的特殊动力学结构，可以满足特定的空间科学任务的需求。以美国的“阿尔忒弥斯”计划为例，提出把Gateway空间站部署在地月系统的近直线晕轨道(NRHO)上，为载人登月实现中转[3-4]。

对CRTBP来说，quasi周期轨道相比周期轨道是更丰富且普遍的存在[5]。在一条周期轨道的附近存在大量的quasi周期轨道，它们不仅具有周期轨道的众多优点，而且增广的自由度扩展了轨道的设计空间，quasi周期运动也是对高精度动力学模型更好的近似[6]。此外，由于分布在高维的不变环面上，使得其在轨道转移及编队飞行等方面更具有先天的动力学优势[7]。基于以上特性，以往的平动点任务也多次采用了quasi周期轨道作为任务轨道，比如NASA的SOHO[8]和“阿尔忒弥斯”[9]等。随着未来平动点飞行任务的科学需求与约束日益复杂化，quasi周期轨道能够提供更加灵活的标称轨道参考，具有广阔的应用价值。

然而，quasi周期轨道更加复杂的动力学特性给计算带来了更大的难度，尤其是对大幅值quasi周期轨道而言。已有不少学者研究了quasi周期轨道的计算问题，提出了半解析法和全数值法两大类方法。Farquhar等[10]最先采用Lindstadt-Poincaré摄动法给出了quasi-Halo轨道的三阶近似解析解，这种方法的精度较为有限，后续需要配合数值方法进一步修正。Gómez等[11]采用摄动法计算了Halo轨道附近的quasi-Halo轨道，他们构造了轨道的25阶近似解析解，并提出多步打靶的思想进一步对解析解进行修正，该方法可以得到较为准确的quasi-Halo轨道，但是解析解的构造较为繁琐，且通用性较低。Jorba等[12]提出用中心流形约化的方法，以Fourier级数的截断形式计算quasi周期轨道。然而，无论是摄动法还是Fourier级数，都存在一定程度的截断与近似，后续以此为初值进一步用数值方法修正时，收敛域较小，一般只能给出中心周期轨道附近很小幅值范围内的quasi周期轨道。

随着计算机的发展，全数值方法逐渐取代半解析法，成为quasi周期轨道的主流计算方法。Howell等[13]提出全数值的微分修正算法用于计算Lissajous轨道，但是得到的并不是不变环面意义下的严格quasi周期轨道。Mondelo[14]提出采用Fourier级数对2维不变环面的不变曲线进行参数化描述，以此实现数值计算，但是该方法计算效率较低，他们使用并行计算进行加速。Kolemen等[15]提出多Poincaré截面法，通过截断Fourier级数把截面上闭合的轨道参数化，通过Newton迭代使得闭合的轨道满足特定的约束条件，以此计算L2附近的quasi周期轨道，该方法具有较低的计算成本，在靠近混沌的区域依然具有较高的收敛性，不过他们并未对其他类型轨道的适用性进行分析。Schilder等[16]提出用偏微分方程来计算quasi周期轨道的不变环面，但是求解偏微分方程较为耗费计算资源。Olikara等[17-18]基于频闪映射法，使用Fourier级数计算高维环面上的不变曲线，成功计算了圆型和椭圆型限制性三体系统的quasi-Halo轨道。Baresi等[19]综合比较了偏微分方程法、多Poincaré截面法和频闪映射法的特点。McCarthy[7]在Olikara等工作的基础上，计算了等能量、等频率比、等映射时间三种quasi周期轨道族，该方法在计算Jacobi矩阵时较为复杂。Lujan等[3]基于频闪映射法，对地月系统L2点quasi-Halo轨道进行单参数延拓，在频域研究了全轨道族的特征，并得到了倍周期分岔的几种quasi周期轨道。已有的研究工作表明，数值方法是构造quasi周期轨道的有效手段，然而过去的研究对象一般集中于Halo轨道、Vertical轨道附近小范围的quasi周期轨道，而且较少涉及三角平动点等情况，对于具有多quasi运动方向的轨道也少有研究。

为此，本文旨在研究一种构造大幅值quasi周期轨道的全数值方法，在Olikara等频闪映射法[17-18]的基础上，重点提高方法对不同类型大幅值轨道的通用性和收敛性。该方法采用多Poincaré截面把不变曲面划分为若干段，设定若干约束，再通过微分修正的思想计算不变环面，最后利用数值延拓获得大幅值quasi周期轨道及等映射间隔的轨道族。仿真表明，该方法不仅在计算大幅值的quasi-Vertical等共线平动点轨道时收敛性好，对于三角平动点及多对复特征值的quasi周期轨道同样具有良好的适用性。

1 动力学模型与研究对象

1.1 圆型限制性三体模型

本文基于圆型限制性三体问题进行建模。在会合坐标系，航天器的动力学方程为：

(1)

其中，

(2)

1.2 quasi周期轨道

周期轨道的单值矩阵M的特征值总是成对出现[20]，且其中有一对为实数1，即λ2=1/λ2=1，剩下的两对λi和1/λi(i=1,3)为复数(或实数)。当单值矩阵M具有在单位圆上的复特征值λc时，在周期轨道的附近存在quasi周期运动，这些quasi周期轨道构成了2维不变环面S。2维不变环面S可用两个独立的角度来描述，分别称为经度θ1和纬度θ2，相应的频率为ω1和ω2[18]，如图1所示：

图1 二维不变环面与quasi周期轨道Fig.1 Two-dimensional invariant torus and the quasi periodic orbit

Poincaré截面∑(θ1=θ1p)与2维不变环面S的交集构成一条不变曲线Γ，不变曲线Γ上的状态具有相同的经度θ1p。对于一条不变曲线，quasi周期轨道从该不变曲线出发，积分时间T1=2π/ω1后，会返回至该不变曲线(如图1所示)，T1称为映射时间。

出发点与返回点之间存在角度差ρ，有如下关系：

(3)

图2 中心周期轨道与quasi周期轨道的幅值Fig.2 Amplitude of central periodic orbit and the quasi periodic orbit

本文用quasi周期轨道与中心周期轨道的幅值之比来描述轨道幅值的大小。由于相关研究较为有限，没有统一的标准，本文认为Bx/Ax,By/Ay或Bz/Az三者任意一个大于1.2的quasi周期轨道属于“大幅值”的范畴。

2 环面多步微分修正

由于大幅值quasi周期轨道所在的2维不变环面维度高、非线性强，对数值构造算法的收敛性有较高要求，针对这一问题，本文在Olikara等频闪映射法[17-18]的基础上，提出映射间隔约束的环面多步微分修正算法，该算法对于大幅值的quasi周期轨道具有良好的收敛性和通用性。

在不变曲线Γ(θ1)上等间隔地选取N个纬度θ2i=2πi/N所对应的特征点，其中i=1,2,…,N，这N个特征点的状态称为特征状态，可表示为：

xi=x(t,θ1,θ2i)

(4)

图3以N=5为例展示了特征点的选取原则。

图3 等纬度地在不变曲线上选取5个特征点Fig.3 Five feature points are selected on the invariant curve with equal latitude

为了增强微分修正算法的收敛性，本文选取多个Poincaré截面，把2维不变环面划分为若干段，相应的形成若干条不变曲线，如图4所示。其中，quasi周期轨道从不变曲线1出发，在其他不变曲线满足拼接的约束条件，接着返回不变曲线1。

图4 4个Poincaré截面和4条不变曲线Fig.4 Four Poincaré sections and four invariant curves

为了方便起见，不妨选取等间隔的M个经度θ1j=2πj/M对应的截面，其中j=1,2,…,M，此时每两个不变环面的映射时间间隔为Tf=T1/M。在每个经度θ1j所对应的不变环面上，再以图3的方式等间隔地选取N个纬度，则第j条不变曲线上的第i个特征状态可表示为：

(5)

据此，本文用各不变曲线上所有特征状态的Jacobi常数的平均值，代表quasi周期轨道的Jacobi常数Jq，即：

(6)

(7)

环面的多步微分修正需要满足特定的约束条件：

1)拼接约束。第j=1,…,M-1条不变曲线Γ(θ1j)上的特征状态，积分Tf后，需要与第j+1条不变曲线Γ(θ1,j+1)上的特征状态重合。

2)返回约束。第j=M条不变曲线Γ(θ1M)上的特征状态，积分Tf后，再经过角度变换-ρ，需要与第1条不变曲线Γ(θ1,1)上的特征状态重合。

3)映射间隔约束。每两个不变环面间的映射时间间隔Tf需要等于设定的需求值Td。

映射间隔约束是附加的约束条件，所以本文称之为“映射间隔约束的环面多步微分修正”算法。综合以上三个约束条件，约束变量F可以表示为：

(8)

(9)

R表示角度变换-ρ的算子，即：

R·x(t,θ1j,θ2i+ρ)=x(t,θ1j,θ2i)

(10)

约束变量F(X)对自由变量X的雅可比矩阵为：

(11)

该雅可比矩阵解析形式的分量不易获得，可以采用前向差分或中心差分等数值方法计算近似的雅可比矩阵。

由于自由变量X比约束变量F(X)的维度多1，多步微分修正的迭代过程可使用最小二乘的形式：

Xk+1=Xk-DFT(Xk)[DF(Xk)DFT(Xk)]-1F(Xk)

(12)

可通过如下的“特征值方法”[7]构造自由变量的初始猜想X0。记λc对应的复特征向量为vc，对于周期轨道上的特征状态x*(t,θ1)，沿vc的方向进行摄动δx0=εvc，则不变曲线Γ(θ1)上的任意纬度θ2对应的特征状态x可以近似为：

x(t,θ1,θ2)≈x*(t,θ1)+εvceθ2=

(13)

示意图如图5所示。

图5 特征值方法构造初始猜想的原理示意图Fig.5 Schematic diagram of theprinciple of constructing the initial guess by the eigenvalue method

对于Tf，可以利用周期轨道的周期T来近似，即：

(14)

对于角度差ρ，取沿特征向量方向的摄动量δx0，根据单值矩阵M的性质，积分一个周期后摄动量为：

(15)

通过与式(13)对比，角度差可以近似为：

(16)

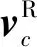
3 环面的数值延拓

当摄动量ε中等偏小时，上述特征值方法能够给出适当的自由变量的初始猜想，环面的多步微分修正算法收敛性较好。但是，当摄动量ε超过一定的程度，自由变量的初始猜想不再准确，受其制约，环面的多步微分修正算法无法保证收敛，此时可以使用延拓法计算quasi周期轨道族，实现计算大幅值轨道的目的。延拓法利用已有的quasi周期轨道的信息构造新的初始猜想，故相比特征值方法更加准确。

3.1 自然参数延拓法

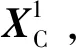
(17)

图6 NPC和PAC两种算法计算quasi周期轨道族的流程图Fig.6 Flow charts for calculating the quasi periodic orbital families of NPC and PAC

本文选择环面的角度差ρ作为延拓变量，由于目标是构造等映射间隔的quasi周期轨道族，因而把映射间隔的需求量Td设为固定值。(下文所述的NPC延拓法都是以环面角度差ρ为延拓变量，并且固定映射间隔需求量Td)

3.2 伪弧长延拓法

NPC延拓法在特征曲线回折处会出现失效的情况，采用伪弧长延拓法(Pseudo-arclength continu-ation,PAC)进行延拓可以解决这一问题[7,21]。伪弧长延拓法给约束变量增加了一个维度，增广的约束变量为：

(18)

增广的雅可比矩阵为：

(19)

自由变量初始猜想的构造形式为：

(20)

此时，增广约束变量与自由变量的维度相同，微分修正的迭代过程为：

Xk+1=Xk-DG-1(Xk)G(Xk)

(21)

为了实现计算等映射间隔的quasi周期轨道族，伪弧长延拓法的计算过程中，Td始终是固定值。使用伪弧长延拓法计算quasi周期轨道族完整的流程如图6(b)所示。

NPC和PAC两种延拓法均固定映射时间间隔的需求值Td，因此，族内每条轨道都具有相同的映射时间T1。NPC的优点是延拓步长s有明确的物理意义，代表族参数ρ的改变量，而PAC的延拓步长s没有明确的物理意义。NPC的缺点是将在族参数ρ达到极值时延拓失败，而PAC的延拓进程则不会受到极值的制约。综上所述，两种延拓法都可以计算quasi周期轨道族，也都有各自的优缺点，可以互补使用。

4 数值仿真与分析

本节将以地月CRTBP系统的L1点Vertical轨道、L4点Vertical轨道、L4点Axial轨道、远距离逆行轨道(Distant retrograde orbit,DRO)等为中心周期轨道，利用映射间隔约束的环面多步微分修正算法，考虑NPC与PAC两种延拓法，设计各中心周期轨道对应的quasi周期轨道族。地月CRTBP系统的参数及中心周期轨道的初值见表1。

表1 地月CRTBP系统的参数及中心周期轨道的初值Table 1 Parameters of the Earth-Moon CRTBP and initial states of the central periodic orbit

4.1 quasi-Vertical轨道族算例

NPC与PAC具有不同的延拓机理，因此计算出的轨道族将存在差异。本部分以L1点的Vertical轨道为中心周期轨道，在相同仿真参数的条件下，对比NPC与PAC的计算结果，相关仿真参数见表2。

表2 quasi-Vertical轨道族的仿真参数Table 2 Parameters of the quasi-Vertical orbital family

表2中，NPC的延拓步数80是能保证算法收敛的最大步数，即步数再增加，算法将发散；PAC的延拓步数38再增加，计算出的轨道与上一个步长无明显差别，因此人为地不再增加步数，结束延拓进程。图7给出了NPC与PAC两种方法延拓过程的Poincaré截面，每个黑色实心圆点代表quasi-Vertical轨道穿过xy平面一次。可以看出，随着延拓的进行，截面的y向幅值逐渐增大。最后一个延拓步长所对应环面称为族末端环面，PAC族末端环面的By/Ay为47.4，而NPC族末端环面这一值为39.2，即PAC轨道族末端环面的y向幅值比NPC轨道族更大。

图7 两种方法延拓过程的Poincaré截面Fig.7 Poincaré sections of the two continuation processes

两种延拓方法给出的都是等映射间隔的quasi-Vertical轨道族，然而Poincaré截面与族末端环面呈现差异的原因是，NPC在族参数ρ减小到一定程度时延拓失败，而PAC不受族参数ρ的制约，故给出的是完整的轨道族。图8给出了两种方法的轨道族的Jacobi常数、映射时间间隔Tf、ρ等特征参数之间的差值与幅值Bx之间的关系，当幅值Bx增大到0.0475时，NPC算法终止。Tf的差值始终为0，说明两个轨道族具有相同的映射时间间隔，其他两个特征参数差值的量级非常小，综合起来说明两个轨道族的自由变量基本一致，两种方法给出的是同一个轨道族，区别在于PAC的是完整的轨道族，而NPC的是部分的轨道族。

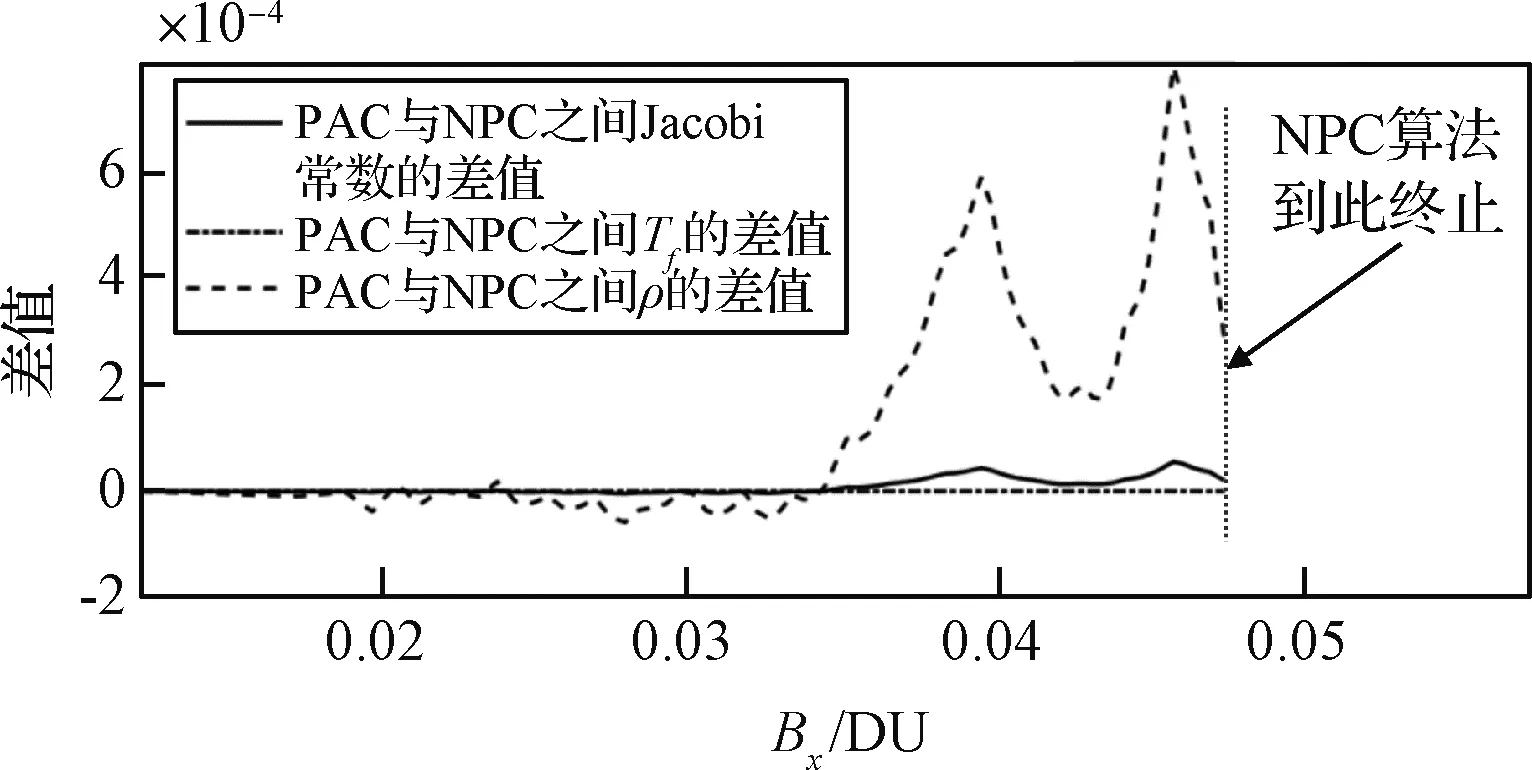
图8 两种轨道族特征参数之间的差值与幅值的关系Fig.8 Relation between difference of characteristic parameters and amplitude for the two orbital families

4.2 三角平动点quasi周期轨道族算例

前面分析了两种延拓法对于L1点的Vertical轨道的适用性，本部分以L4点的Vertical轨道和L4点的Axial轨道为中心周期轨道，采用能给出完整轨道族的PAC算法进行延拓，验证算法对三角平动点quasi周期轨道族的适用性，相关仿真参数见表3。

表3 三角平动点轨道族的仿真参数Table 3 Parameters ofthe triangular libration point orbital family

图9(a)是L4点quasi-Vertical轨道族末端环面，Jacobi常数为2.6183，x向幅值比为8.34。图9(b)是L4点quasi-Axial轨道族末端环面，Jacobi常数为2.1744，x向幅值比为1.37。

图9 quasi-Vertical和quasi-Axial轨道族末端环面Fig.9 Terminal invariant torus of quasi-Vertical and quasi-Axial orbital families

可以看出，对于L4点quasi-Vertical和quasi-Axial轨道族，族末端轨道与中心周期轨道的x向幅值比都超过了1.2，说明算法对计算三角平动点大幅值quasi周期轨道具有良好的适用性。

4.3 多对复特征值的quasi周期轨道族算例

以上算例所选取的中心周期轨道，只有一对在单位圆上的复特征值，所以只有一个quasi周期运动的方向，单对复特征值也是以往的研究所较多涉及的。但是，CRTBP还存在具有两对在单位圆上的复特征值的轨道，比如DRO轨道等，这些轨道相应地具有两个quasi周期运动的方向。

近年来，DRO轨道因其良好的稳定性，在月球空间站、小行星防御等空间任务中得到了广泛的研究[22-23]。本算例以目前研究较多的2∶1共振DRO轨道为中心周期轨道，采用PAC算法进行quasi周期轨道族的延拓，分析其两个quasi周期运动方向的特性。由于PAC算法生成的是等映射时间间隔的轨道族，因此族内每条轨道的映射时间T1都等于中心DRO轨道的周期，所以生成的quasi-DRO轨道依然具有2∶1共振特性。相关仿真参数及2∶1共振DRO轨道的6个特征值见表4。

表4 2∶1共振quasi-DRO轨道族的仿真参数Table 4 Parameters of the 2∶1 resonance quasi-DRO families

对于特征值λ3和1/λ3，quasi周期运动的方向在xy平面内，相应地，quasi周期轨道也在xy平面内。图10(a)是xy平面内quasi-DRO轨道族的末端环面和轨道，y方向的幅值比为1.28。

对于特征值λ1和1/λ1，quasi周期运动的方向在xy平面外，图10(b)是xy平面外quasi-DRO轨道族末端环面和轨道，它是三维的轨道，即z方向具有quasi周期运动的分量。因为中心DRO轨道不具有z向幅值，不妨用Bz/Ax来描述幅值的大小，该条轨道的这一参数为0.35。由于具有z方向的运动分量，相比传统的平面DRO轨道，它作为任务轨道更具有天然的优势，其一，轨道仍然具有2∶1的共振特性；其二，通过选取适当的z向幅值等参数，可以规避日食及运行到月球背面时的通信遮挡问题[24]。

图10 面内和面外quasi周期运动方向的轨道族末端环面Fig.10 Terminal invariant torus of planar and out-of-plane quasi-periodic motions

综合比较各种quasi周期轨道族末端环面3个方向的幅值比，见表5。几乎每种周期轨道族末端环面都有1个方向的幅值比大于1.2，说明本文的数值构造算法能够适应较多类型的大幅值quasi周期轨道。

表5 quasi周期轨道族末端环面3个方向的幅值比Table 5 Amplitude ratio of 3 directions for terminal invariant torus of quasi-periodic orbital family

5 结 论

本文提出了一种利用映射间隔约束的环面多重微分修正算法，结合NPC或PAC计算大幅值quasi周期轨道及轨道族的策略。本文方法能够有效地解决共线平动点、三角平动点、多对复特征值等情况下大幅值quasi周期轨道及轨道族的数值计算问题。