采用自适应Woodbury公式的框架结构高效动力分析与易损性计算方法

余丁浩 李钢 李宏男

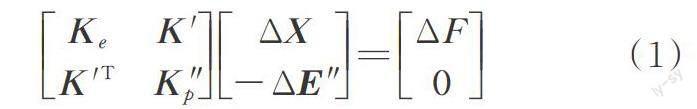
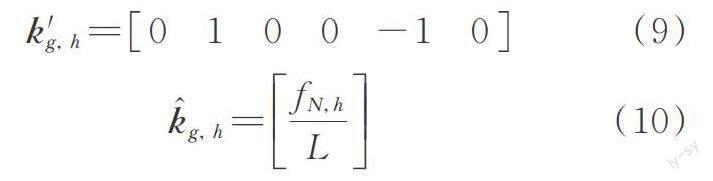
摘要 地震易损性分析是评价工程结构抗震安全性的重要手段，但在计算过程中通常需进行大量的动力时程分析，这导致其计算效率通常较低。该文旨在建立框架结构强震下的高效动力分析与倒塌易损性计算方法。使用纤维梁单元建立框架结构数值分析模型，引入隔离非线性理论进行局部材料弹塑性行为模拟，并通过对考虑P?Δ效应的几何刚度进行矩阵分解和摄动变换，提出了能够同时对局部材料弹塑性行为和几何非线性行为进行隔离表达的纤维梁模型控制方程，结合Woodbury公式进行控制方程求解，所提方法在结构动力非线性分析时能够避免整体刚度矩阵的反复更新，显著提升了求解效率；为克服动力Woodbury公式对时间步长选取的限制，进一步建立不同时间步长下该公式中相关系数矩阵的预处理机制和自适应调度机制，提出了基于自适应Woodbury公式的框架结构高效动力分析方法，在此基础上结合多条带法，建立了结构倒塌易损性曲线的快速计算方法。使用一个9层框架结构验证了所提方法的高效性和准确性。

关键词 易损性分析; 框架结构; 高效动力分析方法; Woodbury公式; 隔离非线性有限元法

引 言

对建筑结构在强震下的抗震性能进行快速准确评估对于保障结构安全性具有重要现实意义。结构抗倒塌能力作为避免强震下出现人员大量伤亡的最终防线，可通过倒塌易损性曲线或以其为基础发展而来的抗倒塌性能指标（如倒塌安全储备系数）进行评价，其中易损性分析通过考虑影响结构地震反应的不确定性因素，能够较为合理地描述结构在不同强度地震下的倒塌概率。

当前已发展出多种易损性分析方法，如增量动力分析（Incremental Dynamic Analysis，IDA）方法、云图法等［1?4］，其中以IDA方法最具代表性，该方法通过选取一组能够表征地震动不确定性的地震记录，将每条地震记录按照某个强度指标（IM）进行多次调幅并对结构进行相应动力时程分析，可以确定结构在不同地震记录下的倒塌点及其概率分布。然而，上述方法均需涉及数十乃至上百次的非线性地震反应分析，计算效率较低。在对于结构抗倒塌性能进行评价时，相应易损性曲线的计算通常仅需关注结构倒塌点，而较小地震强度下的地震反应数據并不需要参与计算，鉴于此，近年来相继有学者提出多种能够快速计算结构倒塌易损性的方法［5?6］，这些方法大多通过减少地震反应分析次数的方式提高倒塌易损性的计算效率，如截断IDA方法、多条带法等，其中截断IDA方法仅需分析部分地震记录引起结构倒塌的地震强度水平［6］，多条带法（Multiple?stripe Analysis， MSA）需在若干特定地震强度下对结构进行多次地震反应分析［7?8］，其所需地震反应分析的次数相较于截断IDA方法更少，该方法中每个地震强度可分别选用代表该强度地震风险水平的不同地震记录进行动力时程分析，亦可选用经调幅的相同地震记录［8］。此外，有学者基于Pushover分析提出了简化的结构倒塌易损性分析方法［9］，尽管此类方法能够避免耗时的动力时程分析，但本质上属于近似分析方法，计算结果包含一定误差。综上可见，虽然以动力分析为基础的结构易损性分析方法可以得到具有较高精度的结构抗地震倒塌能力评价结果，但均需进行大量耗时的地震反应分析。尽管众多学者为减少此类方法的动力分析次数进行了多方面研究，但强震下较为高昂的非线性分析成本依然是制约其被广泛应用的主要障碍，因此，发展更为高效的地震反应分析理论就成为了提高结构抗倒塌性能分析效率的有效途径。

地震作用下结构的塑性变形通常集中于局部区域，对于框架结构，塑性变形主要集中于部分梁、柱构件的端部，相应的结构高效非线性数值分析方法大多利用这一特点展开，例如，孙宝印等［10?12］通过在分析前使用简化弹性梁单元建立结构分析模型，并在分析过程中使用精细化单元对出现弹塑性变形的少量构件进行实时替换，提出了用于框架结构高效分析的数值子结构方法。方明等［13］根据结构局部损伤的分布情况对结构不同部位进行自适应网格细分和自由度缩聚，提出了一种适用于局部非线性问题的动力分析方法。文献［14?16］提出了能够对结构局部非线性问题进行高效求解的显式降维迭代分析法，并基于该方法实现了高效易损性分析。汪梦甫等［17］基于Wilson针对局部非线性问题提出的快速非线性分析方法（FNA），建立了快速增量动力弹塑性分析方法。考虑到结构的局部非线性行为可以转变为初始弹性刚度的低秩摄动表达，众多学者通过引入数学领域中用于低秩摄动问题快速求解的Woodbury公式，提出了多种高效的局部非线性分析方法［18?26］。文献［18?24］将拟立法中的变形分解思想与有限元理论相结合，并引入额外非线性自由度，提出了具有较好适用性的隔离非线性有限元法，该方法使用Woodbury公式对控制方程进行求解，能够在迭代计算过程中有效避免传统非线性分析方法所需的大规模整体刚度矩阵反复更新和分解，极大提高了结构非线性分析效率，同时也结合算法复杂度理论证明了该方法中Woodbury公式的效率优势。随后，文献［20］基于该方法提出了纤维梁单元模型，实现了对一般框架结构的高效非线性分析。

既有基于Woodbury公式的分析方法主要由材料非线性问题发展而来，本文主要关注框架结构在强震下的高效动力分析和倒塌易损性计算，为此，还需进一步考虑结构的几何非线性影响，虽然当前已有多种较为成熟的几何非线性分析格式可供使用，如完全拉格朗日格式、更新拉格朗日格式、共旋坐标法等，但由于结构几何非线性具有全局性特征，与Woodbury公式对于非线性变形的局部化要求相悖，因而该公式难以直接用来进行高效分析。近期Li等［21］参考完全拉格朗日格式，结合隔离非线性法理论提出了一种用于几何非线性行为模拟的近似Woodbury求解方法，虽然该方法相较于传统求解方法能够实现更为高效的分析，但其需在分析过程中根据结构几何位形的变化对控制方程中的整体刚度项进行多次更新，且对Woodbury公式的修改也在一定程度上增加了求解过程的计算复杂度。此外，在进行地震反应分析时，Woodbury公式中结构整体刚度项为包含计算时间步长的有效弹性刚度，为实现基于Woodbury公式的高效分析，结构整体刚度项及与之相关的系数矩阵不能随意改变，这导致分析过程中时间步长难以根据地震激励和结构非线性状态的变化而实时变化，而使用较小的时间步长将引起计算步数增多，最终使得整体分析效率难以得到有效保障，当涉及到倒塌易损性分析这类需考虑大量不同地震记录和高强度激励的计算问题时，这一点显得尤为突出。尽管文献［27］曾结合Woodbury公式提出一种能够实现时间步长随地震强度变化的IDA分析方法，但其中时间步长参数的确定依赖分析者经验判断，因而适用性有限。综上可见，基于Woodbury公式的非线性分析方法具有数学基础严格、适用性好、计算效率高等特点，然而，为充分发挥其效率优势，实现框架结构高效地震倒塌易损性分析，还需对几何非线性模式方法和运动方程求解方法进行更为深入的探索。

本文仅考虑对框架结构在强震下的抗倒塌性能具有显著影响的几何二阶效应（即P?Δ效应），通过对相应几何刚度进行矩阵分解和摄动展开，并进一步与既有的纤维梁单元隔离材料非线性控制方程进行融合，提出了能够对材料弹塑性行为和几何二阶效应同时进行隔离表达的纤维梁模型控制方程，该方程可使结构整体刚度项在分析过程中保持不变，进而可以直接采用Woodbury公式提升方程求解效率。在此基础上，提出了一种用于高效非线性地震反应分析的自适应动力Woodbury求解方法，进一步结合多条带法实现了框架结构的快速倒塌易损性分析，所提方法通过在前处理阶段预先计算出对应于不同时间步长的有效弹性刚度和相关系数矩阵，并在实际分析时引入时间步长和相应系数矩阵的自适应更新与调度机制，能够克服动力分析时Woodbury公式对时间步长选取的限制，充分发挥其高效计算优势，有效提升框架结构倒塌易损性分析的效率。

1 基于隔离非线性的纤维梁模型

本文基于李钢等［20，24］提出的隔离非线性纤维梁单元建立结构数值分析模型，该单元模型最初仅考虑了材料弹塑性行为的模拟。使用图1所示框架结构对该单元基本原理和相应Woodbury求解方法进行说明。图1（b）为截面纤维材料的弹塑性分解过程，可以看出，任意时刻的材料应变增量均可基于其初始弹性模量分解为线弹性应变增量与非线性应变增量两部分，通过将截面中各纤维材料的应变进行集成，可进一步实现截面变形的弹塑性分解，随后，基于插值方法建立单元的截面非线性变形场模型，可在任意计算步中建立如下形式的控制方程

式中 Ke为整体结构的初始弹性刚度矩阵，假设结构模型的位移自由度数为n，则该矩阵阶数为n×n；ΔX，ΔF和ΔΕ"分别代表结构的位移增量向量、荷载增量向量和截面塑性变形增量向量，其中ΔΕ"的阶数为m×1，m为结构的塑性自由度的数目，由于向量ΔΕ"在集成时仅考虑产生塑性变形的截面，因此m与塑性区域的规模有关；K'和K′′p为与局部塑性行为有关的系数矩阵，其阶数分别为n×m和m×m，其中K'与结构中当前产生塑性变形的区域位置有关，K′′p与塑性截面切线刚度有关。

通过对塑性自由度进行凝聚，式（1）可以转化为初始弹性刚度的低秩摄动形式：

式中 等号左边括号中表达式的计算结果代表了结构切向刚度，对于框架结构，地震下其非线性变形通常集中在部分梁、柱构件的端部，塑性变形的局部化特征显著，此时有m?n，从而可引入Woodbury公式对控制方程进行高效求解，如下式所示：

其中：

式中 （K′′p?Kinf）称为Schur补矩阵，其阶数为m×m。

由于结构整体刚度矩阵在整个非线性分析过程中保持弹性，仅需在分析前分解一次即可，因而式（3）的主要计算消耗将集中于m×m阶小规模Schur补矩阵的更新和分解。这表明Woodbury公式的使用可以避免传统非线性分析方法所需的大规模整体刚度矩阵实时更新和分解，取而代之的是对一个规模极小的Schur补矩阵进行相应运算，从而极大提升了结构非线性分析效率。可见，该方法本质上实现了大规模结构非线性问题的降维分析，其高效性也主要来源于此，当结构规模较大或计算工况较多时，该方法的效率优势将尤为明显。

2 考虑P-Δ效应的纤维梁模型隔离非线性控制方程

框架结构中各构件在出现几何变形后由轴向荷载引起的二阶效应（即P?Δ效应）是地震下引发并加剧结构倒塌的主要因素，本文提出了一种将结构几何二阶效应与材料弹塑性行为进行统一隔离表达的方法，以使结构刚度在倒塌易损性全过程分析中保持不变，从而充分利用Woodbury公式的效率优势。

以图2所示的二维梁单元为例，AB为单元初始位置，A0B0为单元变形后位置，图中fN代表作用于单元两个端结点上的轴向力，uν1和uν2分别为单元两端结点沿y方向的位移。本文使用下式构造考虑P?Δ效应的单元简化几何刚度：

式中 L代表单元长度。

上式表明，当仅考虑P?Δ效应时，单元几何刚度仅与其轴向力有关。当进行结构地震反应时，由于各单元之間存在复杂的相互作用，单元轴力并非恒定。考虑到动力分析前通常需施加用于模拟结构自重作用的静力荷载，因此，对于某个单元，可将地震反应分析过程中任意计算步的单元轴向力分解为如下两部分：

式中 fN，v代表结构自重作用引起的单元轴力；fN，h代表当前计算步中单元轴力与fN，v的差值，对于柱构件，该部分轴力主要用于抵抗由地震作用产生的倾覆力矩。

基于式（6）给出的轴力分解表达式，可将式（5）给出的刚度项kg进一步分解为如下形式：

式中 kg，v和kg，h分别代表考虑fN，v和fN，h时产生的单元几何刚度。

由于结构模型一旦给定，各单元在自重作用下的轴向力即可求出，因而式（7）中的刚度项kg，v将在地震反应分析过程中保持不变，而kg，h代表了由轴力变化引起的几何刚度扰动。对kg，h进行摄动变换，可将式（7）改写为如下形式：

其中：

式（8）代表单元几何刚度的摄动展开。将各单元几何刚度进行集成，可建立考虑P?Δ效应时整体结构几何刚度矩阵Kg的摄动展开表达式：

式中 Kg，v代表结构自重对几何刚度的贡献，可将其看作为动力分析时结构几何刚度的初始状态；K'g， h和K?g， h分别由各单元系数矩阵k'g， h和k?g， h集成得到，其中K?g， h为对角矩阵。

将式（11）与前述仅考虑材料弹塑性行为模拟的摄动式控制方程（即式（2））相结合，即可得到同时考虑材料弹塑性和P?Δ效应的摄动式结构控制方程，进一步参考从式（1）到（2）的过程，可反推出如下形式的隔离非线性控制方程：

其中：

式中 ΔΣ′′代表虚拟的几何非线性影响向量，其中的每一项均代表一个虚拟的几何非线性自由度；Keg为考虑几何非线性影响后的整体刚度项，代表了在动力分析初始时刻的结构整体刚度，该矩阵在动力分析过程中将始终保持恒定。

本文方法通过对几何刚度进行分解，可以使整体刚度项在分析过程中保持初始状态不变，在分析过程中由各单元轴力变化导致的几何刚度变化的影响，通过额外引入的虚拟几何非线性自由度予以考虑，其在控制方程中与表征彈塑性影响的塑性自由度一并被隔离表达。式（12）与式（1）具有完全一致的矩阵特征，可直接采用Woodbury公式求解。

由于本文方法仅考虑了P?Δ效应的模拟，几何刚度仅与各单元轴力有关。在构造上述隔离非线性控制方程时，若在某个计算步中某个单元轴力相较于初始状态不发生变化，则该单元将不会引起几何刚度的改变，相应几何非线性自由度可直接从控制方程中消除。然而，通常大部分单元的轴力在动力分析时并不会保持恒定，这将产生较多的非线性自由度，并导致在使用Woodbury公式进行求解时由于Schur补矩阵的阶数偏高而不利于充分发挥其高效性。考虑到在实际地震反应分析过程中，轴力变化较大的单元通常仅存在于结构的局部区域内，相应的单元几何刚度改变也较为明显，而其他大部分单元的轴力仅在小范围内浮动，几何刚度的变化并不明显，其对最终计算结果的影响也较小，本文使用下式在每次迭代求解时对各单元轴力的变化程度进行判别，以便于仅激活少量对计算结果影响显著的几何非线性自由度：

式中 EA为单元截面的弹性轴向刚度。

式（17）所得计算结果实质上代表了由轴力改变量引起的弹性截面轴向应变。进一步引入预先设定的状态阈值λth，在某个迭代步中若某个单元满足条件λp>λth，则相应几何刚度将根据式（6）～（8）推导过程参与控制方程中相关矩阵的集成和Woodbury公式求解，若不满足上述条件则忽略单元几何刚度摄动项的影响，即使用kg，v近似表示单元几何刚度（即若λp≤λth，则令kg≈kg，v），此时该单元不产生额外的几何非线性自由度。由于使用式（17）对单元状态进行识别后结构非线性自由度可保持在较低的水平，Woodbury公式的高效性能够得到保证。应当指出的是，此时Woodbury公式的计算结果将存在一定的近似误差，但该误差可在迭代求解过程中予以消除，因而上述近似处理并不会显著影响最终分析精度。

3 动力Woodbury求解公式自适应更新方法

3.1 运动方程求解

基于上述框架结构的隔离双重非线性控制方程式（12），可建立如下增量形式的结构运动微分方程：

式中 M代表结构的质量矩阵；CR为阻尼矩阵；ΔX¨和ΔX˙分别代表结构的相对加速度增量和相对速度增量；ι为影响系数向量；Δx¨g=x¨g（tk）?x¨g（tk?1），代表第k-1个时间步到第k个时间步的地面加速度增量。

上式中，等号左端的刚度项可始终保持弹性，等号右端增加了考虑结构非线性影响的虚拟荷载项（即K'egΔE′′eg）。将上式等号右端的两项作为施加在弹性结构上的外荷载，使用Newmark平均加速度方法进行数值积分，并结合式（12）中的第二个等式，可建立如下形式的隔离双重非线性动力分析控制方程：

式中 K?eg和ΔF?分别代表结构有效整体弹性刚度和有效荷载增量，相应计算表达式为：

式中 Δt为时间步长；X˙（tk?1）和X¨（tk?1）分别代表结构在第k-1个时间步的相对速度和相对加速度；γ 和β 分别取为0.5和0.25。

引入Woodbury公式，可对式（19）的动力控制方程进行高效求解：

其中：

可以看出，式（22）～（23）与式（3）～（4）在矩阵表达格式上一致，但在荷载项和整体刚度项中包含了时间步长等动力分析相关信息。

3.2 变步长加载策略

为计算结构的倒塌易损性曲线，需选取大量地震记录对结构进行多次高强度激励下的动力时程分析。图3为某典型强震记录的加速度时程曲线，可以看出，虽然其峰值强度较高，但整个时间域中地面高强振动通常仅出现在较小的时间区间内，其余大部分时间区间内的振动强度相对较低。本文所采用的Newmark方法具有无条件数值稳定性，因而在低强度时间区间内可将计算时间步长适当放大，然而，在高强度时间区间内则需减小时间步长，以保证迭代求解过程的计算稳定性。从前文论述可知，为保证Woodbury求解公式的计算高效性，就要求其中的整体刚度项在分析过程中不得随意变化，从式（20）和（23）可以看出，动力Woodbury公式中有效弹性刚度矩阵K?eg及与之相关的系数矩阵K?inf均与时间步长有关，这就对时间步长的选取提出了较为苛刻的要求。若采用固定时间步长进行动力分析，就需选取较小值，以保证高强度时间区间内的迭代稳定性，尽管此种情况下使用Woodbury公式可以提高每个计算步的计算效率，但这将增加分析所需总计算步数，并导致整体分析效率难以得到有效提升。

为实现时间步长的自适应更新，本文首先在结构地震反应分析前预先设定若干时间步长，基于式（20）计算对应的有效弹性刚度，分别进行矩阵分解运算并存储相应计算结果。假设一共预设c个时间步长，并采用LDLT方法进行矩阵分解运算，则有：

式中 Δt_1，Δt_2，…，Δt_c代表c个预设的时间步长（按降序排列）；（K?eg）Δt_i代表对应于第i个预设时间步长的有效弹性刚度；L?Δt_i和D?Δt_i分别为有效弹性刚度（K?eg）Δt_i分解得到的下三角矩阵和对角矩阵。

对于动力Woodbury公式中用于合成Schur补的系数矩阵K?inf（式（23）），可在相应整体刚度项K?eg完成分解后通过多次回代的方式进行计算，该矩阵不仅与时间步长有关，还与结构中进入非线性状态的单元位置有关（原因在于合成该矩阵的K'eg与进入非线性状态的单元位置有关），因此分析过程中需根据时间步长和结构非线性区域的演化而不断更新。为避免在迭代求解过程对矩阵K?inf进行反复的重新计算，同时为提高Woodbury公式的执行效率，本文在分析前预先计算出全局非线性状态下对应于不同时间步长的矩阵K?inf（即假设所有单元均进入非线性状态）并将其存储，为便于区分，使用符号K?INF表示全局非线性状态下的K?inf矩阵，在实际分析时，可根据当前分析步中产生非线性变形的单元编号和选取的时间步长直接从相应K?INF矩阵中提取对应元素合成Schur补矩阵。不同预设时间步长下的K?INF矩阵可使用下式进行计算

式中 K?'eg代表当结构处于全局非线性状态时相应控制方程中的矩阵K'eg。

在进行动力反应分析时，可根据结构的实时非线性状态确定每个计算步的适用时间步长，同时根据所选时间步长從式（24）和（25）的计算结果中调取相应系数矩阵快速构造出对应的动力Woodbury公式并参与迭代求解。考虑到每个计算步求解所需迭代次数能够较为简单、直观地反映出相应时间步长选取的适宜性，本文以当前计算步的迭代次数为判定依据，自适应确定下一个计算步的时间步长，假设某条地震激励下第k个增量计算步的时间步长为Δtk=Δt_i （1 ≤ i ≤ c），且该步计算收敛所需迭代次数为Nk，则本文根据如下原则自适应确定第k+1个增量计算步的时间步长：

① 若Nk小于或等于预先设定的迭代阈值N0（即Nk≤N0），且已连续u个计算步满足该条件（即max｛Nk-u+1，…，Nk｝≤N0），则认为结构此时非线性程度较轻，若当前增量计算步所采用时间步长并非预设时间步长序列中的最大值，可在下一个计算步中增加时间步长，并调用相关系数矩阵，否则不对时间步长进行修改（即若Δtk=Δt_1，则令Δtk+1=Δt_1，否则Δtk+1=Δt_（i-1））。

② 若Nk≤N0，但未连续u个计算步满足该条件（即max｛Nk-u+1，…，Nk｝>N0），则不改变下一个计算步的时间步长（即令Δtk+1=Δt_i）

③ 若Nk大于N0，且小于预设的最大迭代步数Nmax（即N0

④ 若Nk等于Nmax，则认为该计算步迭代发散，若此时所用时间步长并非预设时间步长序列中的最小值，则降低时间步长，调用相关系数矩阵并重新计算该步（即令Δtk=Δt_（i+1）），否则分析终止。

虽然本文方法中式（24）和（25）增加了额外的计算量，但相关计算仅与结构模型有关，因而仅需在动力分析前执行一次，对于结构倒塌易损性分析这类需开展大量地震反应分析的计算问题，额外增加的计算量对于整体计算效率的影响并不显著，这也可以从后文的算例中看出。图4给出了使用本文时间步长自适应更新策略进行大量地震反应分析的实施流程，可以看出，本文引入的额外计算量均仅集中于前处理阶段。

4 倒塌易损性高效计算方法

在计算结构倒塌易损性时，首先需明确结构的倒塌判据，本文参考已有研究，以结构最大层间位移角超过0.1作为易损性分析过程中判定结构倒塌的依据。

使用多条带法计算结构的倒塌易损性曲线，该方法需将选取的地震记录统一调幅至若干强度水平，并计算每个地震强度下的倒塌概率，考虑到在对结构抗倒塌性能进行评价时主要关注其倒塌易损性曲线的前半部分，而较高强度下的数据点缺少实际应用价值，因此该方法无需将地震强度调幅至所有地震记录均引起倒塌的水平［7］，从而仅需进行较少次数的地震反应。假定不同强度下结构倒塌概率符合对数正态分布，则相应倒塌易损性曲线可使用下式计算：

式中 IM代表地震强度指标；P（C|IM=x）代表地震强度为x时的结构倒塌概率；Φ（?）为标准正态概率分布函数；ηc和βRTR分别代表地震倒塌强度的中值和对数标准差，可采用最大似然估计方法对其进行估算，相应求解表达式如下［6?7］：

式中 Nj，Zj分别为地震动水平IM=xj下考虑的地震记录数量和结构倒塌次数；w为倒塌易损性分析过程中考虑的地震强度水平数。

结合本文前述建立的自适应Woodbury非线性高效地震反应分析方法，本文中结构倒塌易损性曲线的快速计算流程如下：

① 建立结构非线性分析模型，在分析前选取若干时间步长，并基于式（24）和（25）计算对应于不同时间步长的相关系数矩阵；

② 确定地震动强度指标IM；

③ 考虑结构所在场地及地震动不确定性，选取多条地震记录，将其统一调幅至不同强度水平xj（j=1， 2， …），首先令j=1，并继续执行下述步骤；

④ 利用本文所提基于时间步长自适应更新的Woodbury分析方法计算地震强度为IM=xj时每条地震记录下的结构反应，若结构在某条地震记录下出现倒塌，则假设提高地震强度后结构在该地震记录下也将发生倒塌，从而该地震记录无需再参与后续地震反应分析，以进一步减小计算量；

⑤ 确定地震强度IM=xj时算得的结构倒塌概率Pk，collapse，当倒塌概率大于某个给定概率阈值Pth时停止分析，并执行步骤⑥，否则，提高地震强度（即令k=k+1）并返回步骤④继续进行地震反应分析；

⑥ 基于式（27）计算地震倒塌强度的中值和标准差，并利用式（26）计算结构倒塌易损性曲线。

本文方法中Woodbury公式的使用可以大幅降低每个求解步的计算量，既有研究表明［22］，该公式的计算复杂度随结构自由度数的增加呈线性增加趋势，但随非线性占比（即m/n，代表了Woodbury公式中Schur补矩阵阶数与结构整体刚度矩阵阶数的比值）的增加呈指数增加趋势，因而对非线性占比的变化较为敏感。相较于传统非线性方法所需的大规模整体刚度矩阵实时更新分解，当非线性占比较小时Woodbury公式具有较高的效率优势，如根据文献［22］建立的算法复杂度计算模型可知，当结构位移自由度数为10000且非线性占比为5%时，Woodbury公式的计算复杂度仅约为整体刚度分解所需计算量的12%，因而其主要适用于激活非线性自由度较小时的情况（m?n）。虽然随非线性占比的增高Woodbury公式的效率优势将逐渐降低，但当前已有学者针对这一问题提出了改进Woodbury公式［19］，使其即使在非线性占比较高时亦能表现出显著效率优势。此外，虽然本文提出的自适应时间步长更新策略能够显著提升动力非线性分析时的迭代稳定性，但在强震作用下依然可能出现由于结构失稳而导致的迭代求解困难，然而，此时结构的侧向变形通常已超过倒塌判定限值，因而不会影响最终易损性计算结果。

5 数值算例

5.1 算例介绍

选取文献［28］中的Benchmark钢框架结构进行倒塌易损性计算，以对本文方法进行验证，该结构地上9层，地下1层，共计5跨，如图5所示。每个梁柱构件划分4个单元，模型共计440个单元，截面纤维材料选用双线性随动硬化本构模型，材料屈服强度根据文献［28］的建议取值，屈服后刚度系数取为0.001。用于确定单元几何非线性状态的阈值λth设为0.001，分析前预设3个时间步长，分别为0.02，0.002和0.0002，用于时间步长自适应更新的相关控制参数分别设为：N0=5，Nmax=10，u=10。

5.2 算法验证

为对本文方法的有效性和准确性进行验证，首先对结构施加一个幅值逐渐递增的正弦加速度激励，同时使用有限元软件ABAQUS对该结构进行对比分析，其中ABAQUS模型的单元划分、材料定义等均与本文方法分析模型相同。图6分别对比了本文方法与ABAQUS在考虑几何非线性和不考虑几何非线性时计算得到的结构一层层间位移角时程曲线，可以看出，考虑几何非线性后结构的位移反应明显增加，不同情况下本文方法与ABAQUS计算结果均基本一致。图6中同时给出了考虑几何非线性时两种方法在一层层间位移角达到0.1时各层的层间位移角分布，可以看出，本文方法在对框架结构进行抗地震倒塌性能分析时的计算精度与ABAQUS基本相当，这表明本文采用考虑P?Δ效应的几何非线性刚度及针对几何非线性提出的摄动展开模拟方法能够满足框架结构抗倒塌性能分析的精度需求。图7给出了本文方法分析过程中时间步长随计算步数的变化（考虑几何非线性），可以看出，本文方法仅在结构进入强非线性阶段后进行了一次时间步长的自适应调整。图8给出了本文方法在进行考虑几何非线性分析时算得的结构非线性自由度占比，图中非线性自由度占比最大值和平均值分别仅为12.9%和7.1%，说明本文方法能够将结构非线性自由度占比控制在极小范围内，从而满足Woodbury公式的高效计算要求。

5.3 倒塌易损性

从FEMA P695［29］建议的22组远场地震记录中每组选取一条地震记录进行倒塌易损性分析，共选取22条地震记录。表1给出了所选地震记录的详细信息。考虑到通常将倒塌概率为0.5时对应的地震强度作为评价结构抗倒塌性能的重要依据，为将其包含在计算所得倒塌概率数据范围内，并最大限度地降低所需地震反应分析次数，本例令用于终止动力分析的倒塌概率阈值Pth等于该值，以地面峰值加速度（PGA）为地震强度指标，在分析过程中将初始地震强度设为5 m/s2（即令x1=5 m/s2），每次调幅将PGA增加5 m/s2，最终PGA调幅到25 m/s2，由于本文方法在进行某个地震强度下的动力时程分析时自动排除了较低地震强度分析时出现倒塌的地震记录，最终共计进行了97次动力时程分析，图9（a）绘制了所有地震激励下结构最大层间位移角随地震强度的变化，图9（b）为最终得到的结构倒塌易损性曲线。

本文方法的总计算耗时为1560.3 s，其中前处理阶段（包括模型载入以及基于式（10）和（11）计算相关系数矩阵）耗时3.54 s，仅占总计算时间的0.227%，这说明本文方法在前处理阶段引入的额外计算对总体分析效率的影响极小。此外，在所有地震反应分析中，Woodbury公式的计算耗时共计115.5 s，仅为总计算耗时的7.4%，其余计算消耗主要用于单元状态确定及执行其他迭代求解所必须的程序代码，本文方法由于能够避免整体刚度的更新和分解，迭代求解过程中用于方程组求解的计算耗时（对于本文方法为Woodbury公式计算耗时）降低到了可忽略不计的水平。为进一步验证本文方法的计算高效性，选取表1中的4号地震记录。表2给出了分别使用本文方法和基于固定时间步长的Woodbury公式对算例结构进行不同强度地震反应分析的计算耗时，可以看出，地震强度较低时，使用较大的固定时间步长即可完成分析，此时固定时间步长法与本文方法的计算耗时基本相当，然而，当PGA增大至25 m/s2时，由于结构出现强非线性导致使用固定时间步长将出现迭代不收敛现象，为此需将时间步长缩小至0.002 s才能保证顺利完成分析，尽管此时每个计算步中Woodbury公式均可实现高效计算，且Woodbury公式的总计算耗时也较少，但过多的计算步数使得整体计算耗时显著高于本文方法，这主要是由于较多的计算步数使得单元状态确定所需计算耗时大幅增加。这表明本文方法能够显著提升强震作用下的迭代稳定性和整体求解效率，对于倒塌易损性这类需进行大量强震作用分析的计算问题尤为适用。综上可见，本文方法的计算高效性不仅来源于Woodbury公式的使用，还来源于时间步长自适应更新策略对总分析步数的有效控制。

6 结 论

本文结合纤维梁单元基本理论，提出了框架结构考虑P?Δ效应的隔离非线性控制方程，该方程可直接采用Woodbury公式进行高效求解，进一步通过建立动力分析条件下与Woodbury公式数值特征适配的时间步长自适应更新策略，克服了该公式在时间步长选取方面的限制，进一步结合多条带法，提出了一种高效的框架结构倒塌易损性分析方法，本文主要研究结论如下：

（1）为实现基于Woodbury公式的高效计算，需同时满足结构整体刚度恒定和非线性自由度规模小两个条件。本文根据地震反应分析的初始状态对考虑P?Δ效应的几何刚度进行分解并在分析过程中對刚度变化项进行摄动展开，可将结构的几何非线性行为和材料非线性行为进行统一的隔离表达，从而使整体刚度在分析过程中保持不变，这满足了Woodbury公式对于刚度恒定的要求。此外，通过对各单元几何非线性状态进行识别，并仅激活少量对计算结果影响显著的非线性自由度，满足了Woodbury公式对非线性自由度规模的要求。上述基本实施步骤和计算原则亦可推广应用到更为一般的结构几何非线性问题高效分析中，此时需首先结合适当的几何非线性表达格式推导出相应几何刚度矩阵的摄动展开表达式，然后建立对应几何非线性自由度的非线性程度判别模型，通过仅保留少量对计算结果影响较大的几何非线性自由度，即可直接构造出具有隔离局部非线性特征的结构控制方程和相应的Woodbury高效求解公式。

（2）尽管本文所提自适应时间步长更新策略适当增加了前处理阶段的计算量，但由于对结构进行倒塌易损性评价时需进行大量动力时程分析，而前处理相关计算仅需执行一次，因此额外增加的计算量对于整体分析效率的影响极小。

（3）本文方法中Woodbury公式的使用能够保证每个计算步的高效性，提出的时间步长自适应更新策略不仅有助于在结构进入强非线性状态后提高迭代求解过程的收敛性，也能够显著降低总计算步数，从而使得整体分析效率得到大幅度提升。本文方法在地震强度较高时效率优势尤为明显，因此尤其适用于倒塌易损性这类需进行大量强震分析的计算问题。

参考文献

1Vamvatsikos D， Cornell C A. Incremental dynamic analysis［J］. Earthquake Engineering & Structural Dynamics， 2002， 31（3）： 491-514.

2吕大刚， 于晓辉， 王光远. 基于单地震动记录IDA方法的结构倒塌分析［J］. 地震工程与工程振动， 2009， 29（6）： 33-39.

L? Dagang， YU Xiaohui， WANG Guangyuan. Structural collapse analysis based on single record IDA method［J］. Journal of Earthquake Engineering and Engineering Vibration， 2009， 29（6）： 33-39.

3陆新征， 叶列平. 基于IDA分析的结构抗地震倒塌能力研究［J］. 工程抗震与加固改造， 2010， 32（1）： 13-18.

LU Xinzheng， YE Lieping. Study on the seismic collapse resistance of structure system［J］. Earthquake Resistant Engineering and Retrofitting， 2010， 32（1）： 13-18.

4任叶飞， 尹建华， 温瑞智， 等. 结构抗倒塌易损性分析中地震动输入不确定性影响研究［J］. 工程力学， 2020， 37（1）： 115-125.

REN Yefei， YIN Jianhua， WEN Ruizhi， et al. The impact of ground motion inputs on the uncertainty of structural collapse fragility［J］. Engineering Mechanics， 2020， 37（1）： 115-125.

5Hardyniec A， Charney F A. A new efficient method for determining the collapse margin ratio using parallel computing［J］. Computers & Structures， 2015， 148： 14-25.

6Baker J W. Efficient analytical fragility function fitting using dynamic structural analysis［J］. Earthquake Spectra， 2015， 31（1）： 579-599.

7张延泰. 超高层建筑结构地震动强度指标及倒塌安全储备研究［D］. 大连： 大连理工大学， 2019.

ZHANG Yantai. Study on earthquake intensity measures and collapse safety margin for super high-rise building structures［D］ Dalian： Dalian University of Technology， 2019.

8Jalayer F， Cornell C A. Alternative non‐linear demand estimation methods for probability‐based seismic assessments［J］. Earthquake Engineering & Structural Dynamics， 2009， 38（8）： 951-972.

9陆新征， 张万开， 柳国环. 基于推覆分析的RC框架地震倒塌易损性预测［J］. 地震工程与工程振动， 2012， 32（4）： 1-6.

LU Xinzheng， ZHANG Wankai， LIU Guohuan. Prediction of seismic collapse vulnerability of RC frame based on pushover analysis method［J］. Journal of Earthquake Engineering and Engineering Vibration， 2012， 32（4）： 1-6.

10孫宝印，张沛洲，古泉，等.基于数值子结构方法的结构弹塑性分析［J］. 计算力学学报， 2015， 32（4）： 465-472.

SUN Baoyin， ZHANG Peizhou， GU Quan， et al. Numerical substructure method for structural nonlinear analysis［J］. Chinese Journal of Computational Mechanics， 2015， 32（4）： 465-472.

11孙宝印， 古泉， 张沛洲， 等.钢筋混凝土框架结构弹塑性数值子结构分析方法［J］. 工程力学， 2016， 33（5）： 44-49.

SUN Baoyin， GU Quan， ZHANG Peizhou， et al. Elastoplastic numerical substructures method of reinforced concrete frame structures［J］. Engineering Mechanics， 2016， 33（5）： 44-49.

12孙宝印，古泉，张沛洲，等.考虑P-Δ效应的框架结构弹塑性数值子结构分析［J］. 工程力学， 2018， 35（2）： 153-159.

SUN Baoyin， GU Quan， ZHANG Peizhou， et al. Elastoplastic numerical substructure method of frame structure considering P-Δ effects［J］. Engineering Mechanics， 2018， 35（2）： 153-159.

13方明， 王建， 李惠. 自适应模型缩放非线性动力分析方法［J］. 土木工程学报， 2018， 51（S1）： 116-121.

Fang Ming， Wang Jian， Li Hui. An adaptive zooming method for nonlinear dynamic analysis［J］. China Civil Engineering Journal， 2018， 51（S1）： 116-121.

14Su C， Li B M， Chen T C， et al. Stochastic optimal design of nonlinear viscous dampers for large-scale structures subjected to non-stationary seismic excitations based on dimension-reduced explicit method［J］. Engineering Structures， 2018， 175： 217-230

15劉小璐，苏成. 大跨度桥梁地震易损性分析的时域显式法［J］. 振动工程学报，2020，33（4）：815-823.

Liu Xiaolu， Su Cheng. Seismic fragility analysis of long-span bridges based on explicit time-domain method［J］. Journal of Vibration Engineering， 2020， 33（4）： 815-823.

16苏成，李保木，陈太聪，等. 粘滞阻尼器减震结构非线性随机振动的时域显式降维迭代随机模拟法［J］. 计算力学学报，2016， 33（4）： 556-563.

SU Cheng， LI Bao-mu， CHEN Tai-cong， et al. Nonlinear random vibration analysis of energy-dissipation structures with viscous dampers by random simulation method based on explicit time-domain dimension-reduced iteration scheme［J］. Chinese Journal of Computational Mechanics， 2016， 33（4）： 556-563.

17汪梦甫， 汪帜辉， 刘飞飞. 增量动力弹塑性分析方法的改进及其应用［J］. 地震工程与工程振动， 2012， 32（1）： 30-35.

WANG Mengfu， WANG Zhihui， LIU Feifei. Improved method for incremental dynamic analysis and its application［J］. Journal of Earthquake Engineering and Engineering Vibration， 2012， 32（1）： 30-35.

18Li Gang， Yu Dinghao. Efficient inelasticity-separated finite element method for material nonlinearity analysis［J］. Journal of Engineering Mechanics， 2018， 144（4）： 04018008.

19Yu Dinghao， Li Gang， Li Hongnan. Improved Woodbury solution method for nonlinear analysis with high-rank modifications based on a sparse approximation approach［J］. Journal of Engineering Mechanics， 2018， 144（11）： 04018103.

20Li Gang， Yu Dinghao， Li Hongnan. Seismic response analysis of reinforced concrete frames using inelasticity-separated fiber beam-column model［J］. Earthquake Engineering & Structural Dynamics， 2018， 47（5）： 1291-1308.

21Li Gang， Jin Yongqiang， Yu Dinghao， et al. Efficient Woodbury-CA hybrid method for structures with material and geometric nonlinearities［J］. Journal of Engineering Mechanics， 2019， 145（9）： 04019070.

22Li Gang， Jia Shuo， Yu Dinghao， et al. Woodbury approximation method for structural nonlinear analysis［J］. Journal of Engineering Mechanics， 2018， 144（7）： 04018052.

23李钢， 吕志超， 余丁浩. 隔离非线性分层壳有限单元法［J］. 工程力学， 2020， 37（3）： 18-27.

LI Gang， L? Zhichao， YU Dinghao. The finite element method for inelasticity-separated multi-layer shell［J］. Engineering Mechanics， 2020， 37（3）： 18-27.

24李钢， 余丁浩， 李宏男. 基于拟力法的纤维梁有限元非线性分析方法［J］. 建筑结构学报， 2016， 37（9）： 61-68.

LI Gang， YU Dinghao， LI Hongnan. Nonlinear fiber beam element analysis based on force analogy method［J］. Journal of Building Structures， 2016， 37（9）： 61-68.

25Akgün M A， Garcelon J H， Haftka R T. Fast exact linear and non-linear structural reanalysis and the Sherman-Morrison-Woodbury formulas［J］ International Journal for Numerical Methods in Engineering， 2001， 50（7）： 1587-1606.

26Deng L Z， Ghosn M. Pseudoforce method for nonlinear analysis and reanalysis of structural systems［J］. Journal of Structural Engineering， 2001， 127（5）： 570-578.

27郝潤霞， 杨作续， 李钢， 等. 基于拟力法的增量动力分析方法［J］.振动与冲击， 2019， 38（4）： 175-183.

HAO Runxia， YANG Zuoxu， LI Gang， et al. Incremental dynamic analysis method based on force analogy method［J］. Journal of Vibration and Shock， 2019， 38（4）： 175-183.

28Ohtori Y， Christenson R E， Spencer B F， et al. Benchmark control problems for seismically excited nonlinear buildings［J］. Journal of Engineering Mechanics-ASCE， 2004， 130（4）： 366-385.

29Applied Technology Council （ATC）. Quantification of building seismic performance factors［R］. FEMA P695. Washington D.C.， 2009.

Efficient structural dynamic analysis and fragility solution methods for frame using adaptive Woodbury method

YU Ding-hao LI Gang LI Hong-nan

State Key Laboratory of Coastal and Offshore Engineering， Faculty of Infrastructure Engineering， Dalian University of Technology， Dalian 116024， China

Abstract Fragility analysis is of important in the evaluation of seismic safety of building structures under earthquake excitation. Such analysis usually involve a large number of dynamic time history analyses which indicate that the computational process is inefficient. This study focus on developing highly efficient dynamic nonlinearity analysis and collapse fragility analysis methods for frame structure. To this end， this study firstly use the fiber beam column element to establish the numerical model of the frame and use the inelasticity separated theory to model local material nonlinear behavior. The P-Δ effect is simulated by decomposing the corresponding geometric stiffness and formulating the decomposed stiffness as perturbation expansion form. Thus， a novel governing equation of fiber beam column element that can uniformly depict the material nonlinear behavior and P-Δ effect using a separated way is developed and it can be solve by adopting the Woodbury formula directly. Because the proposed method can avoid the repeatedly updating of global stiffness matrix in tradition method， the computational efficient is improved greatly. Then， to overcome the limitation of the dynamic Woodbury formula in the selection of time interval， a preconditioning mechanism and an adaptive scheduling mechanism for the coefficient matrices relating the implementation of Woodbury formula corresponding to various time intervals are established. Based on the above investigation， an adaptive Woodbury solution method for highly efficient dynamic nonlinear analysis of frame structure is presented. Furthermore， by incorporating the multiple-stripe method， a fast collapse fragility analysis method of frame structure can be developed. Finally， the proposed method is verified by a nine-story frame structure.

Keywords fragility analysis; frame structures; highly efficient dynamic analysis method; Woodbury formula; inelasticity-separated finite element method