转化思想在初中数学解题中的应用研究

韩为平

(浙江省宁海县城关中学,浙江 宁波 315600)

利用转化思想解题,不仅有利于学生分析与解决问题,而且还能帮助学生更好地巩固与理解学习的基础知识,以增强新旧知识之间的衔接,增强学生的学习兴趣,提高学生的数学核心素养.

1 转化思想在初中数学解题中应用概述

转化思想就是在研究与解决问题时,通过某种方式对问题进行转化,以达到解决问题的目的.一般来说,是将复杂的问题转化成简单的问题,将难解的问题转化为容易的问题.总之,利用转化思想把陌生化为熟悉、复杂化为简单、抽象化为具体,从而使问题得到解决[1].教学中,学生已具备了一定的基础,在解决各种问题时,也可以判断出选择什么方法进行分析与解答.若教师仍通过固定思维约束学生,不仅会影响到学生的个性化需求,而且还会影响学生学习数学的积极性,从而影响学生的解题效率.而将转化思想用于初中数学解题,有利于学生积极主动地参与到问题的思考与解答中,让学生从多个角度来看待问题,掌握分析与解决问题的方法,使学生实现持续性发展.但是,依据教学存在的问题,教师可依据学生呈现的学习特点,对教学思想与教学策略进行调整,并对学生的思维发展情况进行引导,从而使学生学会转化问题、分析问题以及解决问题,并让学生完善知识体系,为以后的学习奠定扎实的基础[2].

2 转化思想在初中数学解题中的应用策略

2.1 直接转化

直接转化主要指与习题相结合,创设相应的情境,依据学习的知识,将需要解决的问题转化成对应的定理、公式或者基本图形.通过直接转化解答问题,需深度理解题意,特别是挖掘题干中的隐含条件,并与自身的解题经验相结合,经过转化及推理,找到解题思路,有效解决问题[3].

例1 如图1,△ABC中,AB=AC,BC=6,AD⊥BC于D点,AD=4,P是半径为2的圆A上的一个动点,连接PC,如果点E为线段PC的中点,连接DE,DE长的最大值是( ).

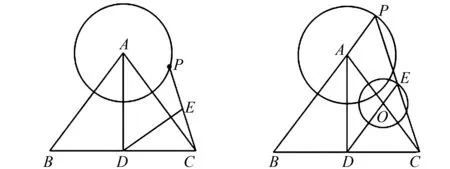
图1 P点运动轨迹图 图2 E点运动轨迹图

A.3 B. 3.5 C.4 D.4.5

解析通过直接法解答问题,可与已知条件相结合,联想有关的定义、图形性质等,构建相应的辅助线,通过更直接的形式呈现参数与线段的关系,以实现问题的高效解决.

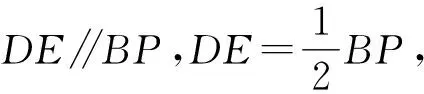
2.2 特殊转化

学生解决数学问题时,都会有自己的思路,而特殊情况,则需依据题中给定的条件,由特定角度入手,思考问题解决的方法.也就是由一般转化为特殊,让学生突破原有的解题限制,引导学生归纳、整理与筛选解题方法,并选择适合的方式,解决问题.

例2 如图3,圆柱体轴截面是正方形ABCD,边长是4,若一只蚂蚁由A点沿圆柱侧面爬至线段BC的中点E,最短路程是多少?

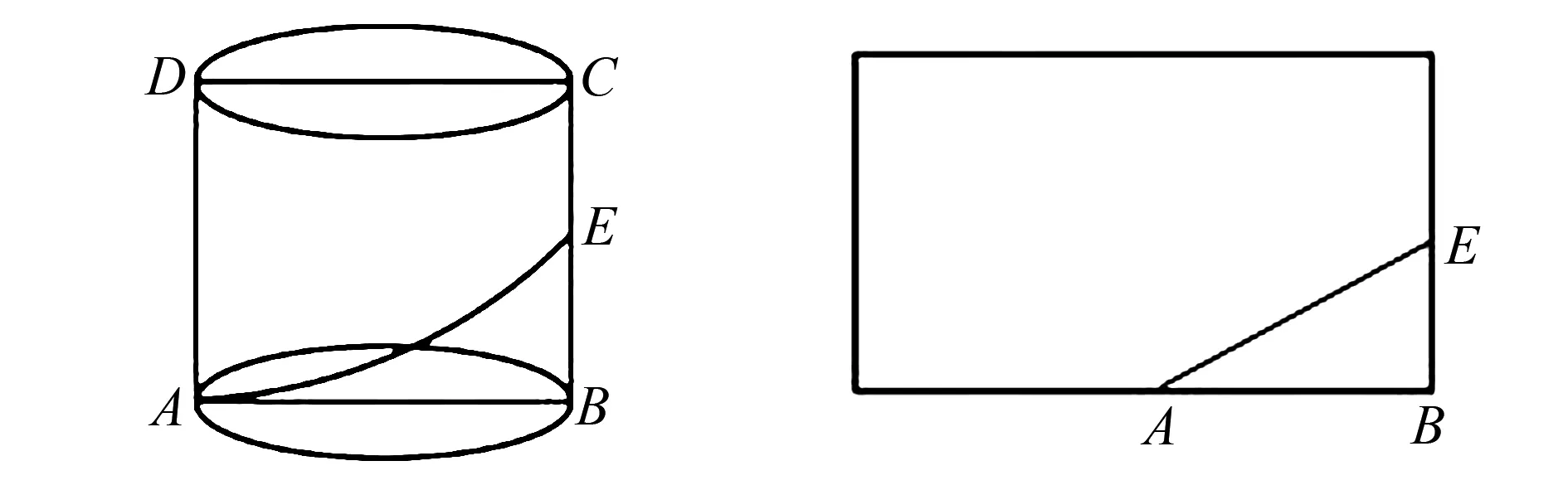
图3 圆柱体ABCD 图4 蚂蚁移动轨迹平面图

解析教师可引导学生将圆柱侧面展开,即把空间问题转化为平面问题,从而解决问题.

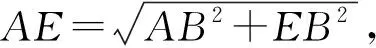
2.3 等式转化

等式转化的思想更多适用于等式问题以及不等式问题,经过转化可有效化简不等式,使题目难度降低.等式转化的方法主要包含了移项法、配方法,将这种方法用于初中数学的解题过程,可使学生形成良好逻辑思维.同时,等式转化的形式是灵活多变的,在教学中,可依据学生的学情让学生通过分析,准确把握等式以及不等式的解题技巧.

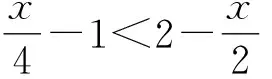
2.4 换元转化

换元主要指在解题中,遇到复杂式子或比较多参数的问题时,可将其替换成另一个参数,充分呈现出参数的规律,降低学生的解题难度.想要使学生准确把握换元在解题中的运用技巧,教师就需选择相应的试题,引导学生对其进行仔细分析,明确换元的具体运用方法,以拓展学生的学习视野,提高学生解题的灵活性.

例4 如图5,长方形ABCD当中,AB=10,BC=6,点E、F为线段BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD的外侧作正方形CFGH与正方形CEMN,如果长方形CEPF的面积是45平方单位,那么图中阴影部分的面积是多少平方单位?

图5 阴影部分面积图

解析在解题时,若直接采用常规的方式求解,难度是十分大的,而通过换元,则能给予学生良好的启发.

解据题意可得:FC=10-x,CE=6-x,由于长方形CEPF的面积是45平方单位,因此,(10-x)(6-x)=45此时,阴影部分的面积是(10-x)2+(x-6)2.运用换元转化,设10-x=a,x-6=b,因此,ab=-45,a+b=4,即(10-x)2+(x-6)2=a2+b2=(a+b)2-2ab=16-2×(-45)=106,因此,图中的阴影部分面积是106平方单位.

2.5 数形转化

数形转化主要指经过数和形之间的灵活转化,实现问题的高效解决.要使学生掌握数形结合思想,并提高解题能力,教师就需将有关的解题技巧讲给学生,特别是对函数图像实施适当的变换,以便实现高效解题.

例5 已知二次函数C:y=ax2-2ax+c的图像过N(1,2),与x轴相交点A(-1,0)和点B,详见图6.

图6 抛物线C

(1)求二次函数C的解析式;

(3)如图7所示,将抛物线C的顶点平移至原点,得到抛物线C1,有直线l:y=kx-2k-4与抛物线C1相交在P、Q两个点,且抛物线C1上存在定点D,使∠PDQ=90°,求D点的坐标.

图7 抛物线C1

综上所述,解题时运用转化思想,能将复杂、陌生的问题转化成简单、熟悉的问题,从而提高学生的解题能力.