例谈阿波罗尼斯圆的应用
吉 磊
(兰州天庆实验中学,甘肃 兰州 730030)
近年来,在各地中考中,对于重难点题型的考查多少都涉及到数形结合解决“极限值”的待定系数问题,在这里就不得不提到非常著名的“阿波罗尼斯圆”(简称“阿氏圆”)理论,这种方法可以帮助学生理解考查题型的设计初衷,从而整合所学相关知识的应用与拓展.
1 阿波罗尼斯圆的定义及定理
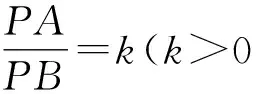
定理如图1,P是平面上一动点,A、B是两定点,PA∶PB=k,M是AB的内分点,N是AB的外分点且AM∶MB=AN∶NB=k,则P点的轨迹是以MN为直径的圆.
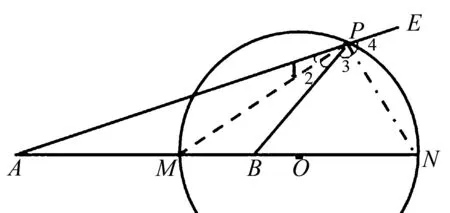
图1 点P轨迹图
2 “阿氏圆”在初中阶段的应用
2.1 阅读材料型(显露阿氏圆)
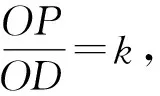
阿氏圆的关键解题步骤:
第一步:如图2,在OD上取点M,使得OM:OP=OP:OD=k;
第二步:证明kPD=PM;第三步:连接CM,此时CM即为所求的最小值.
下面是该题的解答过程(部分):
解在OD上取点M,使得OM:OP=OP:OD=k,
又∵∠POD=∠MOP,∴△POM∽△DOP.
任务:
(1)将以上解答过程补充完整.
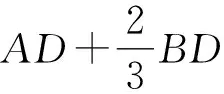
考点:相似形综合题.
专题:几何综合题;应用意识.
分析(1)在OD上取点M,使得OM:OP=OP:OD=k,利用相似三角形的性质以及两点之间线段最短解决问题即可.
(2)利用(1)中结论计算即可.
解(1)在OD上取点M,使得OM∶OP=OP∶OD=k,又∵∠POD=∠MOP,∴△POM∽△DOP.∴MP∶PD=k,∴MP=kPD,∴PC+kPD=PC+MP,当PC+kPD取最小值时,PC+MP有最小值,即C,P,M三点共线时有最小值,
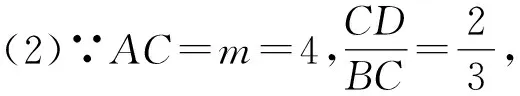
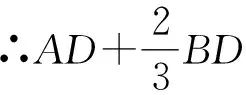
点评本题属于相似形综合题,考查了相似三角形的判定和性质,勾股定理,两点之间线段最短等知识,解题的关键是理解题意,学会用数形结合转化的思想考虑问题,属于中考常考题型.
2.2 非材料阅读型(隐藏阿氏圆)
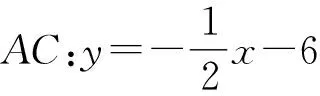
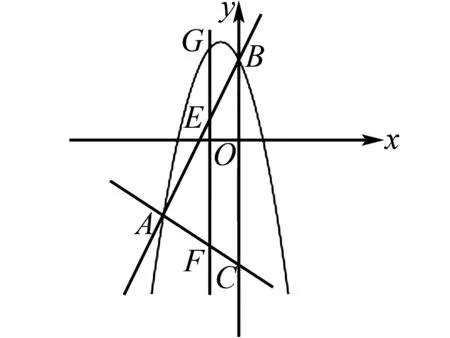
图3 例2题图(a)
(1)求抛物线y=-x2+bx+c的表达式;
(2)连接GB,EO,当四边形GEOB是平行四边形时,求点G的坐标;
(3)①在y轴上存在一点H,连接EH,HF,当点E运动到什么位置时,以A、E、H、F为顶点的四边形是矩形?求出此时点E,H的坐标;
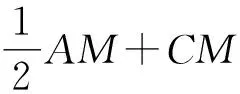
考点:二次函数综合题.专题:综合题.
分析(1)利用待定系数法求出抛物线方程;
(2)先利用待定系数法求出直线AB的方程,进而利用平行四边形的对边相等建立方程求解即可;
(3)①先判断出要以点A,E,H,F为顶点的四边形是矩形,只有EF为对角线,利用中点坐标公式建立方程即可;
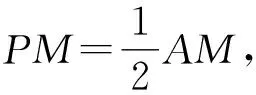
解(1)∵点A(-4,-4),B(0,4)在抛物线y=-x2+bx+c上,
∴抛物线的方程为y=-x2-2x+4;
(2)设直线AB的方程为y=kx+n过点A,B,
∴直线AB的方程为y=2x+4,设E(m,2m+4),
∴G(m,-m2-2m+4),∵四边形GEOB是平行四边形,∴EG=OB=4,
∴-m2-2m+4-2m-4=4,∴m=-2,∴G(-2,4).
(3)①如图4,由(2)知,直线AB的方程为y=2x+4,设E(a,2a+4),
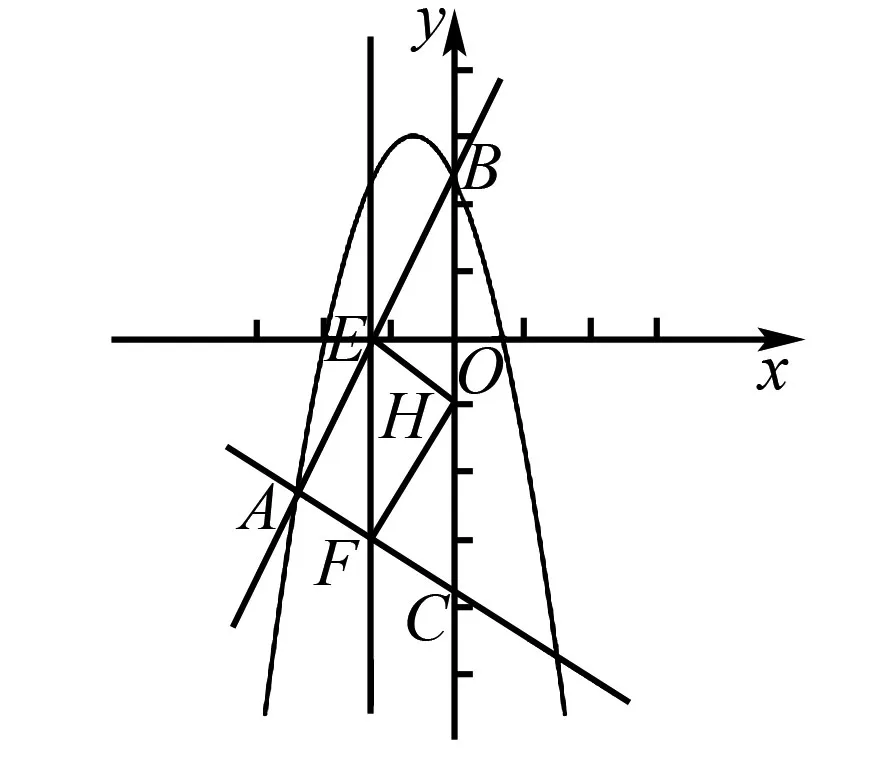
图4 例2题图(b)
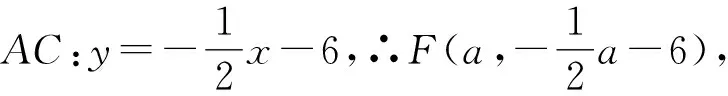
∵以点A,E,H,F为顶点的四边形是矩形,
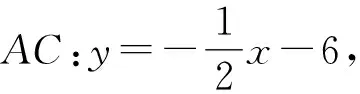
∴AB⊥AC,∴EF为对角线,∴EF与AH互相平分,
∴a=-2,p=-1,∴E(-2,0).H(0,-1);
②如图5,由①知,E(-2,0),H(0,-1),A(-4,-4),
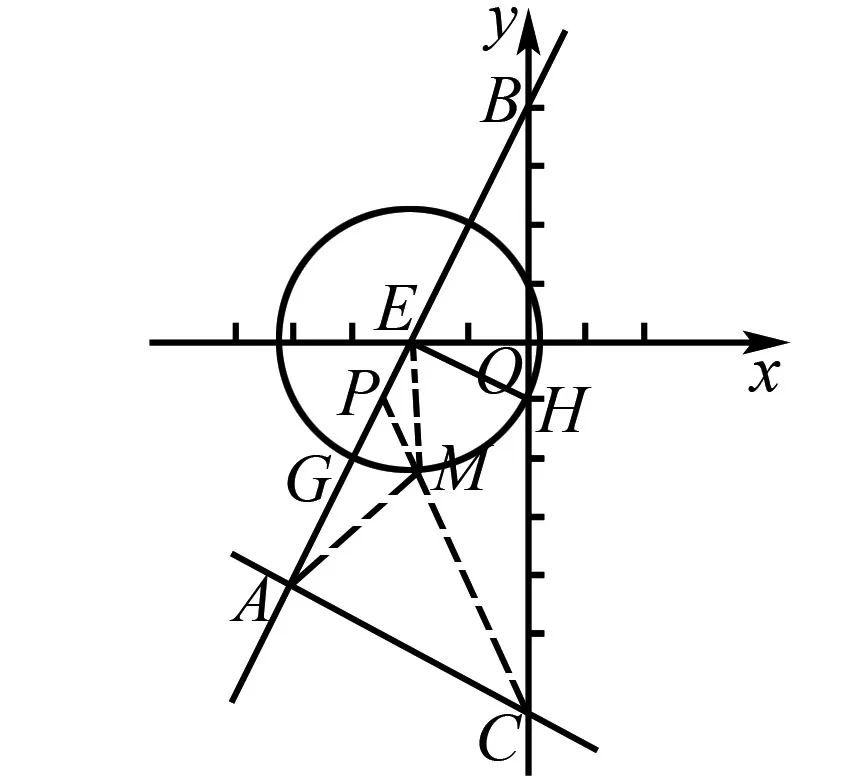
图5 例2题图(c)
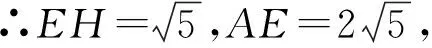
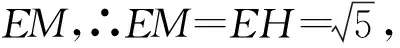
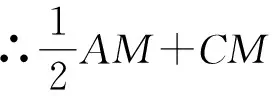
∵E(-2,0),
∴PE2=(p+2)2+(2p+4)2=5(p+2)2,
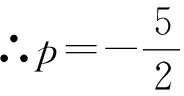
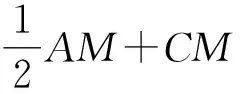
例3(2021·沙坪坝区校级模拟)在四边形ABCD中,AC交BD于点E,△ADE为等边三角形.
(1)若点E为BD的中点,AD=4,CD=5,求△BCE的面积;
(2)若BC=CD,点F为CD的中点,求证:AB=2AF;

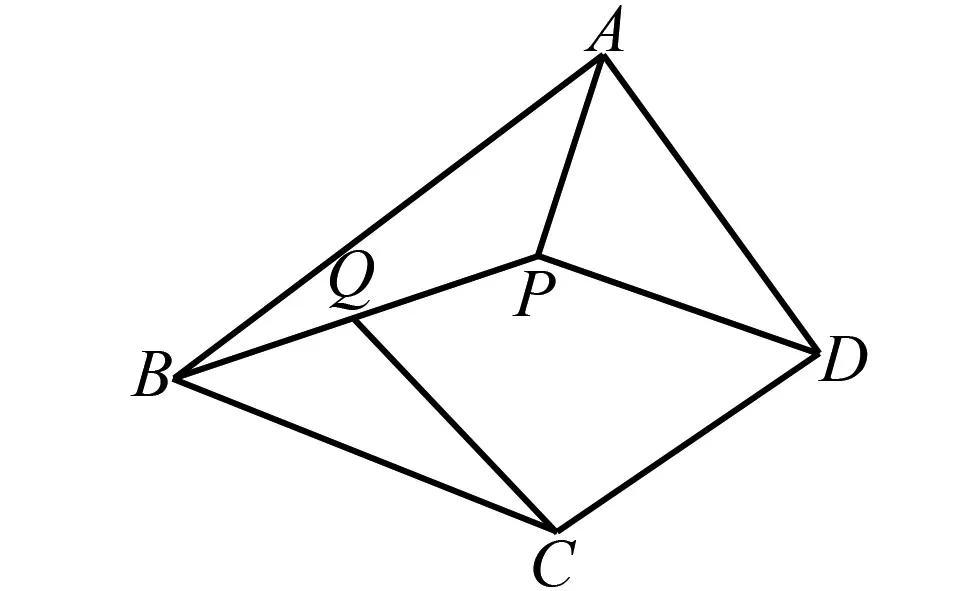
图6 例3题图(a)
考点相似形综合题.专题:图形的相似;推理能力.
分析(1)如图7中,过点C作CH⊥BD于H,设EH=x.利用勾股定理构建方程求出x,即可解决问题.
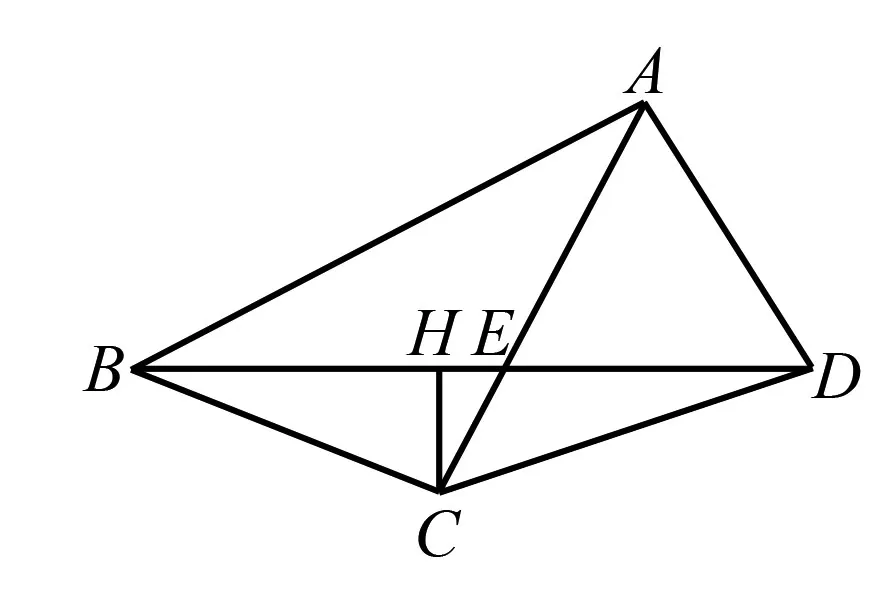
图7 例3题图(b)
(2)如图8中,延长AF到G,使得AF=FG,连接DG,CG,延长GC交BD于T,过点C作CH⊥BD于H.想办法证明△AEB≌△ADG(SAS),可得结论.

图8 例3题图(c)

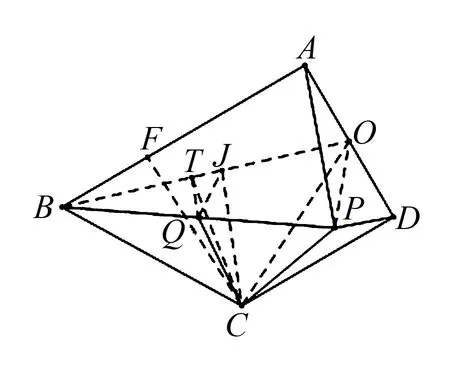
图9 例3题图(d)
(1)解如图7中,过点C作CH⊥BD于H,设EH=x.
∵△ADE是等边三角形,∴AD=DE=4,∠AED=∠CEH=60°,
∵CD2=CH2+DH2,∴25=3x2+(x+4)2,
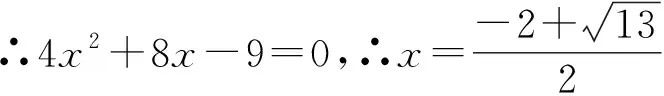
(2)证明:如图8中,延长AF到G,使得FG=AF,连接DG,CG,延长GC交BD于T,过点C作CH⊥BD于H.
∵AF=FG,CF=FD,∴四边形ACGD是平行四边形,
∴AC∥DG,GC∥AD,∴∠CAD+∠ADG=180°,
∵△ADE是等边三角形,
∴AE=AD,∠AED=∠ADE=∠EAD=60°,
∴∠AEB=∠ADG=120°,∴∠CGD=∠EAD=60°=∠GDT,
∴△DGT是等边三角形,∴DG=DT,∠CTE=∠CET=60°,
∴△CET是等边三角形,∴CT=CE,∠CTE=∠CET=60°,
∵CB=CD,CH⊥BD,∴BH=DH,TH=EH,∴BT=DE,
∴BE=DT=DG,∴△AEB≌△ADG(SAS),∴AB=AG=2AF.
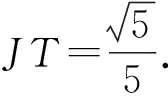
连接QT,TC.∵AB∥CD,∠BAD=90°,∴∠ADC=90°,
∵CF⊥AB,∴∠CFA=90°,∴四边形AFCD是矩形,
∴AD=AF,∴四边形AFCD是正方形,
∵CF=CD,∠CFB=∠CDO=90°,∴Rt△CFB≌Rt△CDO(HL),
∴∠BCF=∠DCO,∴∠BCO=∠DCF=90°,
∵BJ=JO,
∵∠QJT=∠QJB,∴△QJT∽△BJQ,