混合边界约束下矩形薄板自由振动问题的有限积分变换解*

李逸豪, 徐 典, 陈一鸣, 安东琦, 李 锐

(大连理工大学 工程力学系 工业装备结构分析优化与CAE软件全国重点实验室, 辽宁 大连 116024)

0 引 言

弹性矩形薄板广泛应用于土木工程、海洋工程及机械工程等领域,其力学行为一直是学者们的研究重点之一[1-4]．其中,弹性薄板的自由振动问题因其与结构安全高度相关而备受关注,此类问题的解析求解对于结构的快速分析和初步设计具有重要意义．针对板的自由振动问题,其核心是在满足给定的边界条件下,通过求解该问题的高阶偏微分控制方程来获得板的固有频率和振型．然而,由于高阶偏微分控制方程求解过程的复杂性,相关边值问题的解析求解成为一类难题．传统解析方法,例如Navier解法[5]和Lévy解法[6]只能求解对边简支约束下的板问题,其余边界条件下的矩形薄板自由振动问题都不易获得解析解．

实际工程应用对于板的边界约束提出了更高的要求,一边受到混合约束(即同时存在固支、简支或自由中的两种或以上约束)的板进入学者们的视野．例如,在汽车制造领域广泛应用的边缘点焊钢板[7]就是一种典型的混合边界约束板,其点焊位置在分析时可等效为固支边界条件,而同一边上其余位置仍然可视为简支等边界条件．然而,对于这类复杂约束下板的振动问题,传统方法更难以解析求解．针对上述情况,学者们通常采用数值方法来解决相关问题,例如有限元法[8-9]、有限条法[10]、有限差分法[11-12]、边界元法[13-14]、微分求积法[15]、微分容积法[16]等．

上述各类数值方法可以得到满足工程需要的结果,但是解析解仍然具有重要的地位．首先,解析解具有独特的研究价值,例如:其可以作为经验公式以及数值方法对比的基准、快速参数分析和优化的工具,同时也可以为实验提供理论依据等．此外,数值方法所求结果通常为近似解,未必总能达到高精度要求,且求解输入量和输出量较多,过程比较复杂．因此,发展解析方法不仅对理论方法的发展和完善具有重要价值,也对工程结构分析与设计具有重要的指导意义．基于上述背景,本文拟寻求一种新的解析方法来处理混合边界约束下矩形薄板的自由振动问题．

有限积分变换法作为求解数学物理方程的一类重要方法,近年来被笔者等进一步发展,用于板壳力学一般问题的解析求解[17-23]．该方法的思路是:将待求问题的控制方程转换到积分变换域内,得到含有待定系数的位移函数变换式,再由边界条件求解待定系数,最后通过积分逆变换可得到原问题的解析解．因有限积分变换法简洁有效,更容易被工程师所理解和接受,因此有望作为一种通用的理论分析工具．然而,以往关于有限积分变换法的研究均聚焦一边仅有单一约束的问题,对于一边受到混合约束的问题则未能直接应用该方法．为此,有必要将有限积分变换法进一步发展,推广至混合边界板问题的求解中．

本文将有限积分变换与子域分解法结合,首次实现了混合边界矩形薄板自由振动问题的解析求解．首先根据混合边界条件将矩形板拆分为两个子域,然后应用有限积分变换法对两部分分别解析求解,最后通过满足子域间的连续性条件得到该问题最终的解析解．限于篇幅,本文聚焦工程中典型的边缘点焊悬臂板的自由振动问题,将其归结为一边固支-简支混合约束、其余三边自由的矩形薄板自由振动问题进行求解．数值算例表明,无论是固有频率还是振型,本文的结果均与精细有限元及文献结果高度吻合,求解结果的精度不亚于其他复杂的解析方法．本文方法及相关结果有望作为检验各类数值方法精度的对比基准,求解思路也可推广至其他复杂边界约束下的板壳力学问题．

1 薄板自由振动问题的控制方程

基于Kirchhoff薄板理论,矩形薄板自由振动问题的控制方程如下:

(1)

式中W(x,y,t)表示t时刻的挠度;D=Eh3/[12(1-μ2)]表示抗弯刚度,其中E为弹性模量,h为板的厚度,μ为Poisson比;ρ表示薄板密度．根据振动理论,板在自由振动时的动挠度方程为W(x,y,t)=w(x,y)sin(ωt),其中w(x,y)为振型函数,ω为固有频率．将W代入式(1),得到矩形薄板振型微分方程如下:

(2)

板的内力可由w表示为

(3)

其中Mx和My表示Oy轴向和Ox轴向的弯矩,Vx和Vy表示垂直于Ox轴和Oy轴的横截面中的等效剪力．

2 混合边界约束下矩形薄板自由振动问题的有限积分变换解

针对混合边界矩形薄板,本文以“C”“S”“F”分别表示固支、简支、自由这三种边界条件,并从左下方边界开始以顺时针方向通过字母对板命名．限于篇幅,本文以工程中典型的边缘点焊悬臂板、即CS-F-F-F型混合边界矩形薄板为对象进行求解．如图1所示,板的尺寸表示为a,b,b1及b2,其中b=b1+b2;坐标轴Ox与Oy分别与板的下边界与左边界重合．

图1 挠曲电纳米板模型及其坐标系Fig. 1 The flexoelectric nanoplate model and its coordinate system

图1 CS-F-F-F型混合边界矩形薄板图2 CS-F-F-F型混合边界矩形薄板各子域示意图Fig. 1 The rectangular thin plate under CS-F-F-F Fig. 2 Schematic diagram of the sub-domains of CS-F-F-F-F mixed boundary constraints rectangular thin plates

将原板按照边界条件拆分为①、②两个子域,即将原问题拆分为两个子问题,随后对两个子域分别采用有限积分变换法进行求解,在求解过程中每个子域需要满足相应的边界条件及内部连续性条件．各子域的几何模型如图2所示．

图2 挠曲电纳米矩形板的边界Fig. 2 The boundary of a flexoelectric nanorectangular plate

对于每个子域,在矩形域0≤xi≤a,0≤yi≤bi内定义二维有限余弦积分变换如下:

(4)

式中i表示子域编号1、2,wi和(xi,yi)分别表示子域的位移函数和局部坐标,α(m)=mπ/a,βi(n)=nπ/bi,其中m=0,1,2,…,n=0,1,2,…．

逆变换的表达式如下:

(5)

上式中当m=0时,ε(m)=1;当m=1,2,…时,ε(m)=2;当n=0时,ε(n)=1;当n=1,2,…时,ε(n)=2．依据式(4)对式(2)所示高阶偏微分方程各相关项进行二维有限余弦积分变换,可得

(6)

(7)

(8)

(9)

由余弦函数的性质可以消去式(8)中的下划线部分,随后将式(6)—(9)代入式(2)的变换式,可得

(10)

为方便书写,记

(11)

(12)

根据式(3)—(5),并结合Stokes变换[24],可得边界处的弯矩表达式如下:

(13)

(14)

(15)

(16)

同理,可得边界处等效剪力的表达式如下:

(17)

(18)

(19)

根据图2可知:子域①需要满足的边界条件为

(20)

需要满足的连续性条件为

(21)

(22)

则子域①的位移函数积分变换式为

(23)

根据图2可知子域②需要满足的边界条件为

(24)

需要满足的连续性条件为

(25)

(26)

则子域②的位移函数积分变换式为

(27)

综上,还未满足的边界条件和连续性条件有

(28)

(29)

3 典型算例分析

表1 CS-F-F-F方板前十阶无量纲固有频率收敛性研究

表2给出了不同长宽比的CS-F-F-F板在b1=b2条件下的无量纲固有频率．通过与精细有限元分析(采用ABAQUS软件中的S4R单元,网格尺寸为0.002 5a)的收敛结果以及文献的结果对比可知,对于不同尺寸的板,本文的固有频率解均与参考结果吻合良好,证明了本文求解方法的有效性和求解结果的准确性．图3给出了CS-F-F-F方板前十阶振型,结果也与有限元解高度吻合．

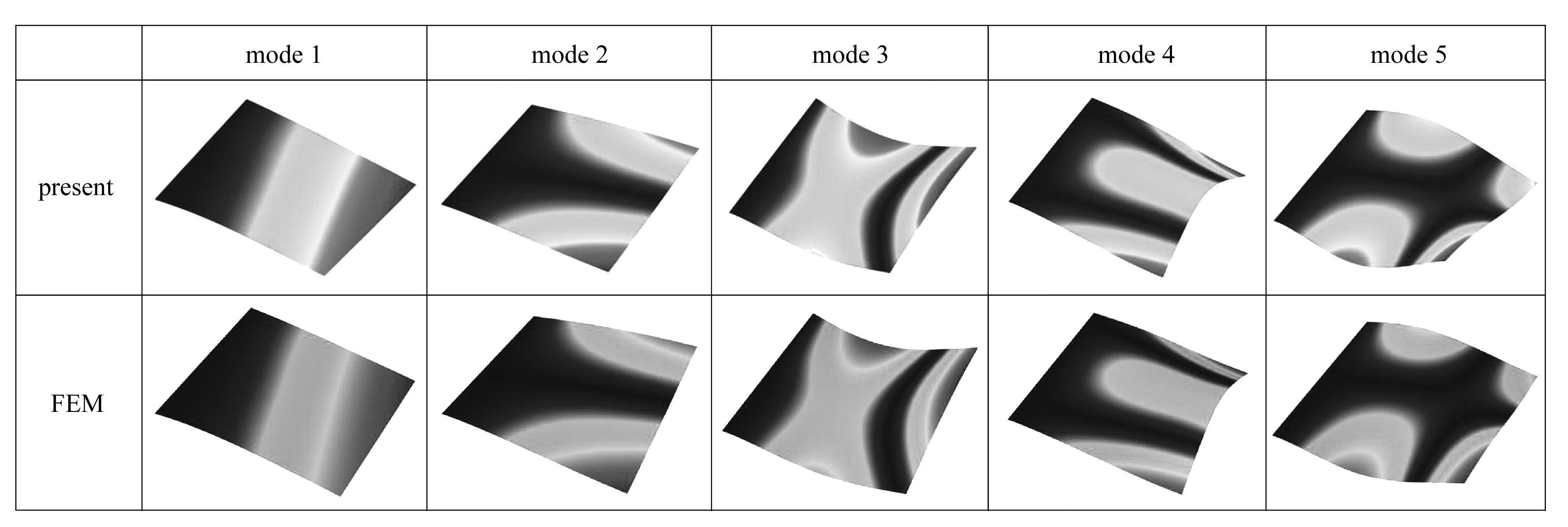
表2 不同长宽比CS-F-F-F板在b1=b2条件下的无量纲固有频率

图3 加载区域Fig. 3 The loading area

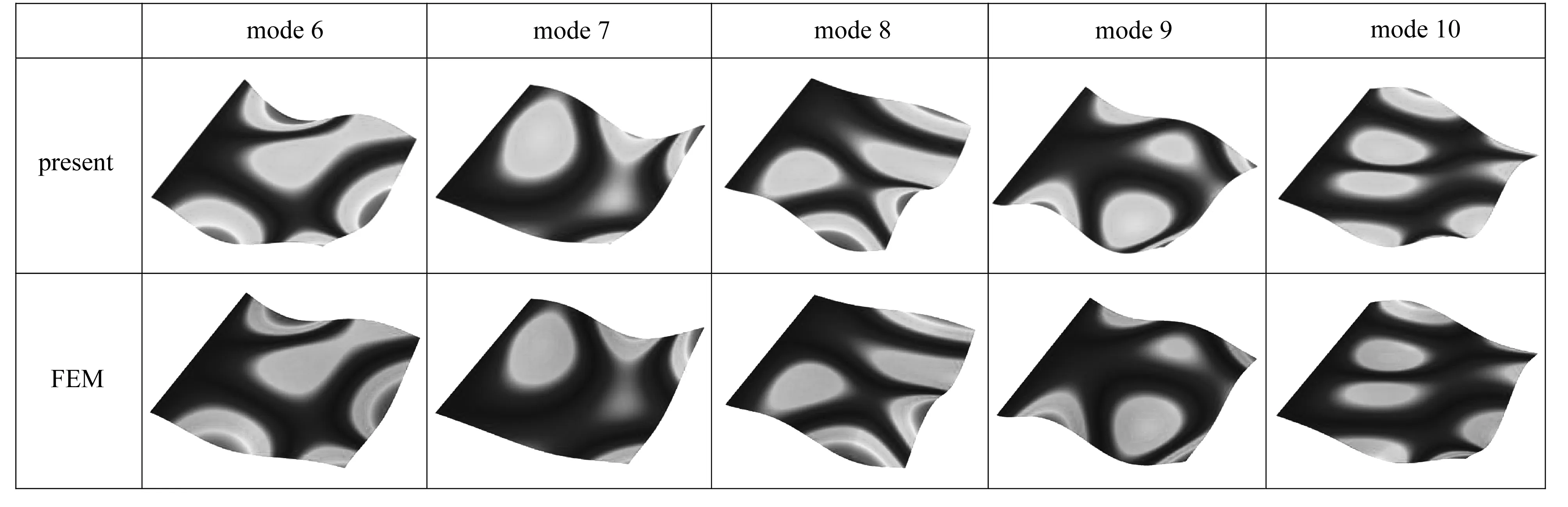
图3 CS-F-F-F方板的前十阶振型Fig. 3 The first 10 mode shapes of CS-F-F-F square plates

4 结 论

本文首次将有限积分变换法扩展至混合边界约束薄板自由振动问题的解析求解,以工程中常见的边缘点焊悬臂板为背景,具体求解了CS-F-F-F型板的自由振动问题．分析过程中采用双余弦形式的积分核对两个子域分别解析求解,最后通过连续性条件获得该问题完整的解析解．本文给出的数值算例表明获得的解析解与精细有限元分析及文献结果吻合良好,证明了求解方法的有效性及所求结果的准确性,同时为检验各类数值方法提供了对比基准．本文发展的有限积分变换结合子域分解的方法在求解过程中无需预先假设解的形式,而是从基本控制方程出发并逐步推导以获得结果,因此是一种严格的求解方法,可为复杂边界约束下板壳力学问题的解析求解提供一种新思路．