一种基于逆幂核主成分的维度约减方法

张红艳

（贵州民族大学数据科学与信息工程学院，贵阳 550025）

0 引言

随着科技的进步和计算能力的提高，越来越多的数据呈现出高维特点，高维数据不仅包含大量的冗余信息，而且处理起来十分耗时。不断增加的数据维度，更会导致所谓的“维数灾难”（dimensionality curse）［1］问题。通过维度约减能有效减少数据特征的数量，提高计算效率。目前，维度约减被广泛应用于机器学习［2］、数据分析、数据可视化、自然语言处理［3］和图像处理［4］等领域。

维度约减可分为线性维度约减和非线性维度约减两种方法。线性维度约减是指通过线性变换将高维数据映射到低维空间中，从而减少数据的维度，同时尽可能地保留原始数据的关键特征。它的典型代表为主成分分析法（principal component analysis，PCA）［5］。PCA 擅长处理线性可分的数据，当数据不可分，或存在缺失、异常等情况时，若仍采用线性维度约减，则数据将丢失原本的结构。因此，Schölkopf 等［6］提出基于核技巧的主成分分析法（kernel principal component analysis，KPCA）。与传统PCA 不同，KPCA 可以通过非线性变换将数据映射到高维空间中，并在该空间中执行PCA，以获取更有效地捕获数据特征的主成分。

KPCA 通过使用核函数计算原始数据点和高维空间中的映射点之间的相似度来获得高维空间中的内积矩阵或距离矩阵，然后对矩阵进行分解以获得主成分和其相关的投影系数。由于核函数的能力，它可以处理高维、非线性和具有任意核心密度的数据集。核主成分分析的核心之处在于核函数的选择［7-8］。因此，构造了一个新的逆幂核函数，并用该核函数对高维数据进行维度约减。通过在四个高维数据集上的实验分析，对比高斯径向基核、多项式核、全变量情况，逆幂核函数的维度约减效果相对更优。

1 核主成分分析

核主成分分析法是一种非线性的数据分析方法，其主要思想是：通过引入非线性变换Φ，将数据由输入空间Rm映射到高维特征空间F，然后在特征空间F中利用PCA 方法进行数据分析和处理。

设样本集X={χ1,χ2,χ3,…,χN}∈Rm通过非线性变换Φ 将样本点χi映射在特征空间F中是Φ(χi),i= 1,2,…,N，将之中心化后，即转换为

可得F空间中的协方差矩阵Σ为

根据

求Σ的特征值λ和特征向量ν。由式（2）知，计算Σ需知道Φ(χi)和Φ(χj)，而Φ又是未知的。但所有的特征向量ν均可以表示为Φ(χ1),Φ(χ2),…,Φ(χN)的线性张成，即

因此，可得

将式（2）、（4）代入式（5），令

得

其中：K为N×N核矩阵，nλi是K的特征值，α=α1,α2,…,αN是对应的特征向量。按一定的标准取前m(m＜N)个特征值和对应的标准化后特征向量α1,α2,…,αm。此时特征空间F中样本点Φ(χi)在ν上的投影为

在进行维度约减时，怎么确定降维后应保留的属性维度d，主要取决于数据集和核函数，不同的数据集和核函数分类预测精度不一样。一般采用包裹式学习算法，即属性维度d的取值与后续机器学习分类算法的表现性能联系在一起，取得的属性维度d应使后续分类算法的分类精度更优［7］。

2 核函数

2.1 常见核函数

由低维空间向高维空间映射带来的困难就是计算复杂度的增加，而核函数正好巧妙地解决了这个问题。这一过程是通过用核函数K(χi,χj)=＜Φ(χi)Φ(χj)＞代替Wolfe对偶问题中χi和χj的点积来实现的。常用的核函数如下:

（1）多项式核：

（2）高斯径向基核：

其中，r,q,γ是核函数参数。r是平移参数，r≥0；q是多项式阶数，常见取值范围为(1,10)；γ是一个超参数，控制数据点在高维空间中的分布情况，常见取值范围为(10-3,103)。

2.2 逆幂核函数

核主成分分析法的关键是核函数的选择是否恰当，不同的数据利用不同的核函数能有效提高维度约减效果，并能有效提高后续机器学习分类算法的预测性能，依据核函数的构造原理，本节构造新的核函数，称其为逆幂核函数。

定义1［9］称二元函数：X× Χ →R 是正定的，如果它是对称的，即K(χ,χ')= K(χ,χ')，并且对任意m∈N（正整数集合），任意χ1,χ2,…,χm∈X,α1,α2,…,αm∈R，都有K(χi,χj) ≥0，即对任意训练数据χ1,χ2,…,χm∈X,K=(κ(χi,χj) )是正定矩阵。

为了证明函数

是核函数，根据定义1，需证明对于任意的训练样本χ1,χ2,…,χm和任意的实数α1,α2,…,αm，都有

其中，K(χi,χj)表示χi和χj之间的核函数。

对于该函数，有以下推导

因此，对于任意的α1,α2,…,αm，有

然后，定义一个矩阵K，其中，第i行、第j列的元素为Kij= K(χi,χj)。因此，式（12）可以写成

其中，a=[α1,α2,…,αm]T是一个m维向量。

因此，要证明该函数是核函数，只需要证明对于任意a，都有aTKa≥0。考虑到K是一个对称矩阵，因此可以使用它对角化的特征值分解来证明。具体地，设K=UΛUT，其中U是一个正交矩阵，Λ是一个对角矩阵，其对角线上的元素λ1,λ2,…,λm表示K的特征值。由于K是半正定矩阵，因此，所有的特征值都非负。现在，将a表示为Ub的形式，其中，b=UTa。因此，有

由于所有的特征值都非负，上述式子的值都非负。因此，对于任意的训练样本χ1,χ2,…,χm和任意的实数α1,α2,…,αm，都有

2.3 核主成分分析维度约减算法

根据核主成分分析原理，其维度约减算法的基本步骤如下：

3 实验结果与分析

实验代码使用R 语言（R-4.2.2）编码实现。实验环境为Windows10 64 bit操作系统，8 GB内存，Intel（R）Core（TM）i5-8250U CPU@1.60GHz 1.80 GHz。数据集详细描述见表1。使用分类精度作为评价不同数据集维度下的机器学习分类方法的分类性能。

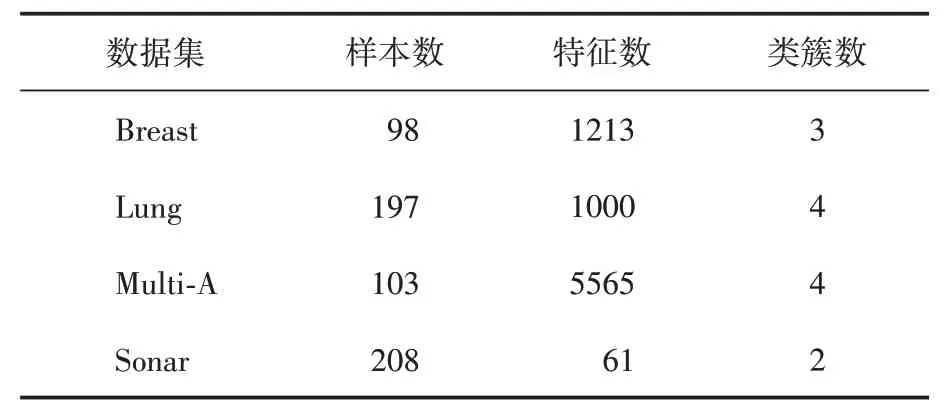
表1 实验数据集描述

3.1 实验设计

为验证逆幂核的分类性能，本文利用新的逆幂核和传统的多项式核、高斯径向基核及全变量对数据集进行维度约减，然后采用支持向量机主流机器学习分类方法对原始数据集及已降维的数据集进行分类预测。

3.2 对比实验结果与分析

本文使用的几种核函数均带有参数，径向高斯（radial basis function，RBF）核函数参数γ，其中δ2=50；多项式（polynomial function，POLYF）核函数参数r,q，其中r= 0；逆幂（inverse power function，IPF）核函数参数c,b。d表示属性维度。由于核函数所包含的参数不多，对每个参数设置一定的范围，然后采用简单的网格搜索法，使得后续分类算法的精度达到最高。在降维后的数据集上进行支持向量机分类预测。同时不对数据进行处理，将全变量（full variable，FV）参与支持向量机（SVM）中，上述几种方法可以记为AV+SVM、POLY+SVM、RBF+SVM、IPF+SVM。其五折交叉验证精度见表2。

表2 不同核函数下SVM的五折交叉验证精度对比

由表2可知，在没有对数据进行维度约减的情况下，直接用SVM 进行分类，其分类精度都比较低，分别为52%、70.52%、19.33%和75.96%。这些情况都表明了支持向量机对高维数据集具有一定的敏感性。因此，需要对数据进行维度约减，可以看到，在用核主成分进行维度约减后，其分类精度较未进行维度约减前有了显著提升。尤其对于数据特征较多的数据集（Multi-A），其分类精度较未进行维度约减前提升较大。但是，不同数据集的核表现性能有较大差异，对比高斯径向基核、多项式核及全变量的情况，运用本文所提出的逆幂核主成分进行的维度约减，其分类精度相对较高，这表明核主成分的维度约减能有效提取原始数据的信息。

4 结语

对于高维数据集，为了提高后续机器学习算法的分类性能，证明了一种新的逆幂核主成分，并基于该逆幂核主成分的维度约减方法，对高维数据集进行维度约减。通过对四个高维数据集的对比实验，得到与传统的高斯径向基核、多项式核及全变量情况的对比研究，结果表明提出的逆幂核主成分的维度约减更加有效地提高了机器学习方法的分类精度。