“三全育人”理念下“数学分析”教学案例

摘 要：本文以“数学分析”中的条件极值为例，在课堂教学设计过程中，引导学生以问题驱动的形式思考和分析问题，融入思政元素，将知识点与辩证思想联系起来，践行“三全育人”理念，提高学生分析问题和解决问题的能力，逐步培养学生理论联系实际的能力。

关键词：数学分析；三全育人；条件极值

A Teaching Case of Mathematical Analysis under

the Concept of "Three Wide Education"

—Taking the Conditional Extremum as an Example

Lin Wenxian

College of Mathematics andStatistics，Hanshan Normal University GuangdongChaozhou 521041

Abstract：Taking the condition extremum in mathematical analysis as an example，in the process of classroom teaching design，this paper guides students to think and analyze problems in the form of problemdriven，integrating ideological and political elements，to link knowledge points with dialectic thought，to practice the idea of three wide education，to improve students' ability to analyze and solve problems，and to develop students' ability to combine theory with practice.

Keywords：three wide education；mathematical analysis；condition extremum

为深入贯彻落实习近平新时代中国特色社会主义思想和党的十九大精神，落实立德树人根本任务，围绕“培养什么样的人，如何培养人以及为谁培养人”的根本问题，充分发挥课堂教学主渠道育人作用，全面加强“课程思政”建设，全面提高课程育人质量，全面提升立德树人成效，践行“三全育人”教育模式.

“数学分析”是近代数学的基础，是现代科学技术中应用最广泛的一门学科；它是大学本科数学与应用数学专业学生必修的最重要的基础课程，“数学分析”以学习时间长（三个学期）、知识抽象、逻辑性强为主要特征，它对于学生良好的数学素质的形成以及后续课程的学习起着至关重要的作用.因而，在传授知识的同时，如何将“课程思政”融入“数学分析”这一抽象理论课程的教学环节之中，是摆在我们面前的难题.本文将以反常积分概念为案例，在教学内容的设计中进行一些探索，以期达到抛砖引玉的作用.

1 教学设计

1.1 教学背景

多元函数极值是多元函数微分学的重要组成部分，是一元函数极值的推广.上一章已学习多元函数的极值问题，其极值点的搜索范围是目标函数的定义域，这类问题称为无条件极值，而在许多极值问题，其极值点的搜索范围还受到各种不同附加条件的限制，这类问题称为条件极值问题.条件极值在实际问题中应用非常广泛，并且还能用来证明或建立不等式.

1.2 教学目标

1.2.1 知识目标

理解条件极值概念，掌握Lagrange乘数法的思想.

1.2.2 能力目标

通过本节课的学习，学生要进一步认识无条件极值与条件极值的关系，培养学生的化归、类比和分析等数学思想，提高分析与解决实际问题的能力.

1.2.3 思政目标

将“思政元素”融入专业课堂，将多元函数极值问题比喻成人生的起伏，引导学生思考.一个国家、一个单位、一个部门以及一个人的一生，本质上都是在追求极大值和最大值.同学们在高中是优秀的，是所在班级的极大值或者最大值，但是当来到大學之后，是否还是极大值或者最大值呢？要想达到极大值或者最大值，就需要同学们付出辛勤的汗水，努力拼搏.同时，以后进入社会，也要明白天外有天，人外有人的道理.不要骄傲自满，使学生建立良好的人生观、价值观、世界观.

1.3 教学重点

掌握Lagrange乘数法，应用Lagrange乘数法计算条件极值.

1.4 教学难点

理解Lagrange乘数法的数学思想.

1.5 教学方法

问题驱动教学法，讲授法.

1.6 教学过程

1.6.1 复习旧知

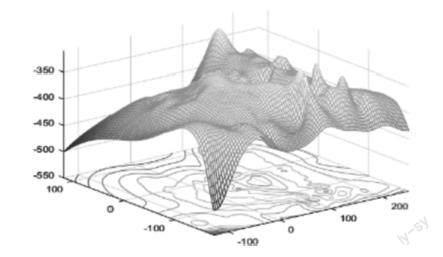
通过下面的曲面图复习多元函数极值概念，并产生人生启示：人生何尝不像一张曲面，极大值在高峰处取得，极小值在低谷处取得.人生总会有起有落，现实生活中的“低谷”和“高峰”都是暂时的，在遭遇挫折处于“低谷”的时候不能悲观绝望，因为“低谷”往往意味着一段低潮的结束和一个新生活的开始；而在获得成功处于“高峰”的时候也不应骄傲自满，要警惕“高峰”之后随之而来的低潮.所以，要有不怕挫折勇往直前的意志和戒骄戒躁、谦虚进取的精神.

1.6.2 问题引入

要设计一个容积为V的长方体形开口水箱，确定长、宽和高，使水箱的表面积最小.

设水箱的长、宽、高分别为x，y，z，则表面积为S（x，y，z）=2（xz+yz）+xy

水箱容积V=xyz.

这实际上是求函数S（x，y，z）在V=xyz限制下的最小值问题.我们将这类附有条件限制的极值问题称为条件极值问题.我们可以给条件极值一个具有实际意义的解释：一个旅行者沿着一条指定的路线（约束条件）去登山（目标函数），该指定路线未必通过山的最高点，问怎样求出该旅行者所能达到的最高点.

例1：求S（x，y，z）=2（xz+yz）+xy在约束条件V=xyz之下的极值.

解：消元法：从条件式解出显函数z=V/xy，代入目标函数后，转而求解S=2vxy（1x+1y）+xy的普通极值问题.即：

F（x，y）=S（x，y，Vxy）=2vxy（1x+1y）+xy

然后由（Fx，Fy）=（0，0），求出稳定点x=y=32V，并有z=1232V.

最后判定在此稳定点上取得最小面积S=334V.

注：消元法启示：将条件式作显化处理代入目标函数后，将目标函数和约束条件方程浓缩到一个函数式，条件极值就成为无条件极值（把有约束条件变成无约束条件），用以前求普通极值的方法即可.

问题：如果无法将条件式作显化处理时，例1的消元法就无法进行了.

我们要解决的问题：寻找一种不直接依赖消元而求解条件极值的方法.这就是拉格朗日（Lagrange）乘数法.

1.6.3 Lagrange乘数法探源

如果无法将条件式作显化处理时，此法就无法进行了.必须研究不直接依赖消元而求解条件极值的方法.

问题：在约束条件φ（x，y）=0之下，欲求函数z=f（x，y）的极值.

首先，给条件极值一个具有实际意义的解释：一个旅行者沿着一条指定的路线（约束条件）去登山（目标函数），该指定路线未必通过山的最高点，问怎样求出该旅行者所能达到的最高点.（如图）

接着，设由若由条件φ（x，y）=0确定了隐函数y=g（x），使得目标函数成为一元函数z=f（x，g（x））.如果y0=g（x0）且x0是z=f（x，g（x））的稳定点，则P0=（x0，y0）就是所要求的条件稳定点.

利用隐函数定理有dzdx=fx+fy·dydx=fx-fy·φxφy=0，从而，该问题的条件稳定点P0（x0，y0）满足（fxφy-fyφx）|P0=0，这表明f的等高线z0=f（x，y）与曲线φ（x，y）=0在点P0（x0，y0）有公共切线.由此推知，存在比例常数λ0，满足：

fx（x，y）+λφx（x，y）=0，fy（x，y）+λφy（x，y）=0，φ（x，y）=0.

进而得到Lagrange函数为L（x，y，λ）=f（x，y）+λφ（x，y）.由此产生了一个重要思想：通过引入辅助函数L（x，y，λ），把条件极值转化为关于这个辅助函数的普通极值问题，这就是Lagrange乘数法.

1.6.4 应用举例

利用Lagrange乘数法求解例1.

例2：求S（x，y，z）=2（xz+yz）+xy在约束条件V=xyz之下的极值.

解：令Lagrange函数L=2（xz+yz）+xy+λ（xyz-V），并求解以下方程组：

Lx=2z+y+λyz=0Ly=2z+x+λxz=0Lz=2（x+y）+λxy=0Lλ=xyz-V=0

为消去λ，将前三式分别乘以x，y，z，则得：

2xz+xy=-λxyz2yz+xy=-λxyz2（x+y）z=-λxyz

两两相减后立即得出x=y=2z，再代入第四式，得x=y=32V，z=1232V，从而最小面积为S=334V.

例3：抛物面z=x2+y2被平面x+y+z=1截成一個椭圆，求该椭圆到原点的最长和最短距离.

例4：求f（x，y，z）=xyz在条件1x+1y+1z=1r（x>0，y>0，z>0，r>0）下的极小值，并证明不等式：

31a+1b+1c-13abc，

其中a，b，c为任意正实数.

1.7 知识小结

（1）根据问题意义确定目标函数与条件组.

（2）作拉格朗日函数L（x，y，λ）=f（x，y）+λφ（x，y）.

（3）求拉格朗日函数的稳定点，这些稳定点就是可能的极值点.

（4）对每一个可能的条件极值点，据理说明它是否确实为条件极值点.如果已知某实际问题或根据条件确有极值，而该问题的拉格朗日函数又只有一个稳定点，且在定义域的边界上（或逼近边界时）不取得极值，则这个稳定点就是所求的条件极值点.否则，还需要采用无条件极值的充分条件来判定.

2 教学反思

2.1 思政元素

通过讲解曲面图像的人生启示，培养学生认真、上进、拼搏的精神.同学们考入大学，容易松懈，以为自己可以自由地玩耍，有些同学消极对待学习.所以教师要经常鼓励提醒这些同学，不要荒废宝贵的大学时光，要努力学习，认真上进，不断拓宽自己的知识结构，提高自己的能力，这样进入社会才会有竞争力.同时，作为一名教师，教学多年，也很容易有倦怠感，所以也要提醒自己，学习如逆水行舟，不进则退，也要不断提高自己的教学水平，紧跟时代潮流，这样才能更好地完成教学任务.

2.2 教学思考

利用创设合适的问题情境，引入新课内容，以避免学生对内容的突兀感.

在Lagrange乘数法探究过程中，让学生认识数学知识的“形成过程”，有利于学生进一步理解一个数学问题是怎样提出来的，一个数学概念是怎样形成的，一个数学结论是怎样获得和进行应用的，使学生认识到数学就来自我们身边的现实世界，是认识和理解我们生活和工作中所遇到问题的有力武器，同时也使学生获得了数学探究的切身体验和能力.

注意运用几何图像的直观性，帮助学生理解抽象的数学概念，特别是注意文字语言、符号语言和图形语言的相互转换.

结语

在课程思政理念下，教师要把“德育”看作是教育的根本任务，更新观念，深入挖掘，以数学学科知识为载体，发挥数学育人的特殊作用，促进学生树立正确的世界观、人生观和价值观.在专业基础课中，教师如何渗透课程思政？如何发现每个知识点的思政元素？如何提高学生学习知识的积极性？这是高校教师面临的一个课题，任重而道远，是一个值得深入思考和研究的终身课题.

参考文献：

［1］华东师范大学数学科学学院.数学分析（下册）［M］.北京：高等教育出版社，2019.

［2］林文贤.反例在数学分析教學中的作用［J］.高师理科学刊，2008，28（4）：9395.

［3］钟煜妮，林文贤.分部积分法在重积分的应用［J］.高师理科学刊，2015，35（1）：11.

［4］林文贤.高师数学分析课程对学生数学素质的培养［J］.韩山师范学院学报，2005（3）：9295.

基金项目：广东省一流课程《数学分析》建设项目（Z21011）；2021年度韩山师范学院教育教学改革项目（52 1104）；2022年度韩山师范学院质量工程建设项目（E22033）

作者简介：林文贤（1966— ），男，汉族，广东潮州人，本科，教授，从事数学分析的教学与研究。