0-k 膨胀计数回归模型的参数估计与统计检验
李春玉,安博文,李晓天
(1.河北经贸大学数学与统计学学院,河北 石家庄 050061;2.华侨大学经济与金融学院,福建 泉州 362021;3.新疆理工学院经济贸易与管理学院,新疆 阿克苏 843000)
观测数值为自然数的数据就是计数数据,其在生物医学、临床试验、保险索赔、风险管控以及社会科学等方面都得到了广泛应用,因此计数数据的回归预测、统计检验等问题一直是数据分析的热点问题.在实际应用中,0 膨胀现象、0-1 膨胀现象或0-k膨胀现象都较为常见.就0-k膨胀而言,当k取值为0时即为0 膨胀分布,当k取值为1 时即为0-1 膨胀分布.无论是0 膨胀分布还是0-1 膨胀分布均是0-k膨胀分布的特例,因此本文将0-k膨胀计数回归模型作为研究对象.
0-k膨胀现象是指0 和k同时膨胀,样本数据表现为观测值中的0 值和k值频率都较高.0-k膨胀需要满足0 和k同时膨胀,这就要求在回归模型中需要包含两个膨胀参数,一个膨胀参数控制0 膨胀,另一个膨胀参数控制k膨胀.从现有文献来看,部分学者对0 膨胀、0-1 膨胀和0-k膨胀的回归模型都进行了深入研究,例如:Lambert[1]首次基于泊松分布提出0 膨胀回归模型,同时引入协变量对膨胀数据进行解释;Melkersson 和Olssen[2]提出0-1 膨胀泊松回归模型,并结合看牙医次数的统计数据进行实例分析;Lin 和Tsai[3]针对健康调查数据建立0-k膨胀泊松回归模型进行统计分析.上述文献对膨胀模型的建立与参数估计都进行了详细研究,但并未涉及膨胀类型数据的统计检验.如果调查数据仅服从0 膨胀分布或者仅服从k膨胀分布,而在建模过程中依旧采用0-k膨胀分布进行分析,这可能会由于因变量分布设定错误而导致回归结果出现偏差.基于此,本文期望通过统计检验对0-k膨胀进行识别以便精准建模.
回顾之前的相关研究,关于回归系数的估计方法的研究结果如下:Fahrmeir 和Echavarria[4]研究了一类可加的0 膨胀模型,Ghosh 等[5]给出了0 膨胀回归模型的贝叶斯估计法,Zhang 等[6]讨论了0-1 膨胀Poisson 分布的统计性质并给出了回归系数的区间估计,杨亮和孟生旺[7]建立0 膨胀分位回归模型并给出了相关参数的贝叶斯估计结果,Tang 等[8]将0-1 膨胀模型重参数化并给出了EM 算法和贝叶斯算法两种估计方法,夏丽丽和田茂再[9]在0-1 膨胀泊松回归模型的泊松部分建立非参数模型并采用EM算法给出了估计结果,安博文等[10]基于Fisher 信息矩阵给出了0-1 膨胀贝塔- 二项分布参数的置信区间,李春玉等[11]采用EM算法给出了0-1 膨胀贝塔- 负二项分布参数的置信区间.就膨胀参数的统计检验研究结果而言,Broek[12]采用Score统计量对0 膨胀泊松分布的参数进行检验,Moghimbeigi 等[13]通过抽样分布测试了Score统计量的检验功效,Xiang 和Teo[14]采用Wald统计量和LR统计量对0 膨胀泊松分布进行了检验,Hsu 等[15]建立混合权重0 膨胀回归模型并采用Wald统计量进行检验,黄倩[16]采用Score统计量对0-k膨胀泊松回归模型进行检验.刘娱等[17]分别采用LR统计量、Wald统计量和Score统计量对0-1膨胀泊松回归模型进行了检验.
综上所述,本研究将对0-k膨胀回归模型进行参数估计和统计检验,借鉴Tang 等[8]对0-1 膨胀泊松回归模型的设定方法引入隐变量建立0-k膨胀回归模型并基于EM 算法给出回归系数与膨胀参数的估计结果;基于Fisher 信息矩阵构造各个参数的置信区间;采用Wald统计量和LR统计量对0-k膨胀分布是否会出现退化进行检验;以0-k膨胀泊松回归模型为例结合相关数据进行实例分析.
1 模型设定
假设随机变量V服从非膨胀的基础分布,记为V~f(θ|v)(其中θ 表示分布f(θ|v)中原有的参数,和分布膨胀与否无关);引入隐变量B和隐变量C分别控制0 膨胀部分和k膨胀部分,且B~B(1,p)、C~B(1 ,q);要求随机变量V、B和C相互独立.令Y=V(1−B)+k×B(1−C),则随机变量Y所服从的分布即为0-k膨胀分布(简记为ZKI分布).Y与(B,C,V)的对应关系如下
研究样本Y1,⋅⋅⋅,Yn独立同分布于0-k膨胀分布,用y=(y1, ⋅⋅⋅,yn)表示样本的观测数据,则0-k膨胀分布的概率质量函数如式(1).
式(1)中:θi表示非膨胀分布的原有参数,pi为0 膨胀参数,qi为k膨胀参数.经过计算,式(1)的数学期望表示为.当pi>0 且qi=0 时,式(1)退化为k膨胀分布(简记为KI分布);当pi>0 且qi=1 时,式(1)退化为0 膨胀分布(简记为ZI分布);当pi=0 时,式(1)退化为非膨胀的基础分布(简记为NI分布).
将参数θi、pi和qi作为被解释变量,引入协变量zi、xi和wi,假定链接函数为
式(2)中:zi、xi和wi为可观测数据, β、γ 和α 为待估系数,观测数据与待估系数的具体形式如下
2 参数估计
这部分基于EM算法和Fisher 信息矩阵给出0-k膨胀分布回归系数的点估计值与区间估计值.
2.1 点估计
被解释变量y以及协变量z、x和w均可以被观测,隐变量B和隐变量C不可被观测,这里假定其样本数据形式依次为b=(b1, ⋅⋅⋅,bn)和c=(c1, ⋅⋅⋅,cn).由此可以得到扩充数据的对数似然函数为
将式(2)代入式(3)中即可得到含有协变量的对数似然函数.
以下采用EM算法求解式(4)的最大化问题.EM 算法分为E 步和M 步,E 步为计算隐变量B和隐变量C的数学期望,M步为最大化对数似然函数式(4).
E 步:根据文献[8]可以分别计算出隐变量B和隐变量C的数学期望,如式(5)
M步:采用极大似然估计法求解式(4)中的参数.具体过程如式(7)
这里采用Newton-Raphso 迭代计算方程组(7)的数值解,记,则β、γ 和α 的极大似然估计结果为
式(8)中:t表示Newton-Raphso 算法的迭代次数.
2.2 区间估计
用空间A表示样本y的所有观测值,空间A0表示样本y中所有值为0 的观测值,空间Ak表示样本y中所有值为k的观测值.记A中元素个数为n,A0中元素个数为n0,Ak中元素个数为nk.对式(3)和式(4)进行改写,写出不含隐变量的对数似然函数,具体见式(9)
根据式(10)可以计算回归系数β、γ 和α 的Fisher 信息矩阵,记为J.由于回归模型的参数个数为(k+r+m+3),则J为(k+r+m+3)阶方阵.考虑第(ii= 1, ⋅⋅⋅,k+r+m+3)个回归系数o(ioi∈{0, ⋅⋅⋅,},0, ⋅⋅⋅,r,0, ⋅⋅⋅,m}),其对应的Fisher 信息矩阵为,其中
由此可得回归系数oi的方差为
从而,回归系数oi的(1−)置信区间为
3 膨胀参数检验
采用Wald统计量和LR统计量对0-k膨胀分布的膨胀参数进行假设检验.0-k膨胀是指0 和k同时膨胀,因此需要考虑3 种情况:①是否退化为0 膨胀分布;②是否退化为k膨胀分布;③是否退化为非膨胀的基础分布.对此提出3 个假设检验:①是否退化为0 膨胀分布的检验,原假设表述为0-k膨胀分布会退化为0 膨胀分布,则H0为p>0 且q=1,拒绝H0说明该分布不会退化为0 膨胀分布;②是否退化为k膨胀分布的检验,原假设表述为0-k膨胀分布会退化为k膨胀分布,则H0为p<0 且q=0,拒绝H0说明该分布不会退化为k膨胀分布;③是否退化为非膨胀分布的检验,原假设表述为0-k膨胀分布会退化为非膨胀分布,则H0为p=0,拒绝H0说明该分布不会退化为非膨胀分布.
根据式(9)可以计算关于膨胀参数的Fisher 信息矩阵.记
其中
Wald检验统计量和LR检验统计量分别为:
是否退化为0 膨胀分布的检验统计量
是否退化为k膨胀分布的检验统计量
是否退化为非膨胀分布的检验统计量
4 实例应用
这部分以0-k膨胀泊松回归模型为例进行实际应用.取基础分布(其中=),取链接函数(·)=log (·)、(·)=logit (·)和(·)=logit(·),则0-k膨胀泊松回归模型的具体形式为
其中
4.1 回归系数估计
实例数据来源于pscl 包中提供的bioChemists 数据集,bioChemists 数据集以915 名生物化学博士为调查对象,记录了他们在博士后三年期间发表论文数量(ART)、博士后性别(FEM)、是否婚配(MAR)、所拥有5 岁及以下的子女数量(KID)、博士在读学校的声望(PHD)以及他们导师近三年撰写文章的数量(MENT).经过筛选,本文选取ART作为被解释变量,将MENT和KID分别作为泊松部分、0 膨胀部分和k膨胀部分的协变量,具体模型如下
于ART变量而言,观测样本量为915,其中,观测数值为0 的样本量是275,占比为30.05%;观测数值为1 的样本量是246,占比为26.89%;观测数值为2 的样本量是178,占比为19.45%.因此这里依次将k取值为1 和2,分别建立0-1 膨胀泊松回归模型和0-2 膨胀泊松回归模型,具体估计结果如表1、表2所示.

表1 0-1 膨胀泊松回归模型系数估计结果Tab.1 0-1 Coefficient estimation results of expansion Poisson regression model
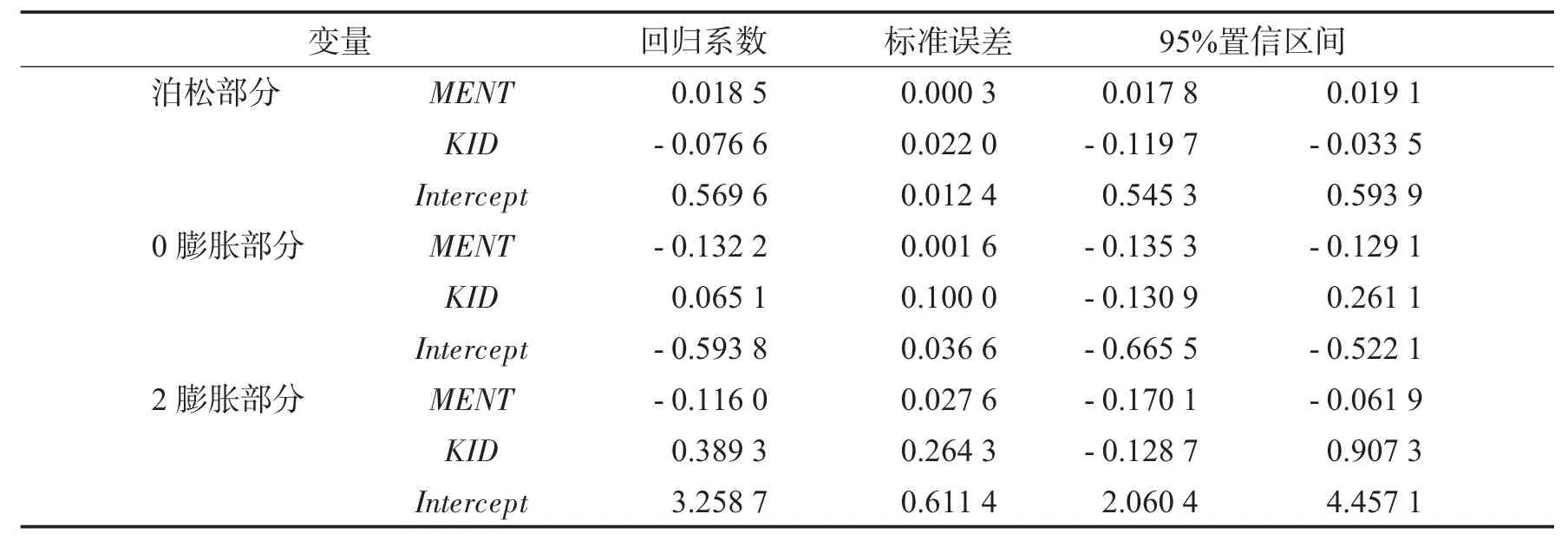
表2 0-2 膨胀泊松回归模型系数估计结果Tab.2 0-2 Coefficient estimation results of expansion Poisson regression model
回归系数的估计结果显示,于0-1 膨胀泊松回归模型而言,泊松部分的ART与MENT呈正向变动关系,即博士后导师发表论文数量越多则博士后发表论文数量也越多,说明博士后导师发表论文会对博士后发表论文产生积极影响;ART与KID呈反向变动关系,5 岁及以下子女数量越多则博士后发表论文数量越少,说明随着5 岁及以下子女数量增加博士后的时间精力被逐渐分散,从而发表论文数量减少.0 膨胀部分的ART与MENT呈反向变动关系,随着博士后导师发表论文数量增加博士后不发表论文的可能性逐渐减小;ART与KID呈正向变动关系,随着5 岁及以下子女数量增加博士后不发表论文的可能性逐渐增大.1 膨胀部分的ART与MENT呈反向变动关系,博士后导师发表论文数量增加会减小博士后发表1 篇论文的可能性;ART与KID呈正向变动关系,5 岁及以下子女数量增加会增大博士后发表1篇论文的可能性.于0-2 膨胀泊松回归模型而言,泊松部分、0 膨胀部分都与0-1 膨胀泊松回归模型的估计结果相近,回归系数的正负号和数量级均未发生明显变化,通过对比两种回归模型也验证了泊松部分、0 膨胀部分估计结果的稳健性.2 膨胀部分,ART与MENT呈反向变动关系,1 膨胀部分MENT的系数为-0.073 8,2 膨胀部分MENT的系数为-0.116 0,随着博士后导师发表论文数量增加博士后发表1篇论文可能性的减弱程度要低于发表两篇论文可能性的减弱程度;ART与KID呈正向变动关系,1 膨胀部分KID的系数为0.211 8,2 膨胀部分KID的系数为0.389 3,随着5 岁及以下子女数量增加博士后发表2 篇论文可能性的加强程度要高于发表1 篇论文可能性的加强程度.
4.2 分布参数估计与膨胀参数检验
这部分对0-k膨胀分布是否会出现退化的现象进行假设检验.在假设检验之前需要计算相关的膨胀参数,表3 和表4 依次给出了0-1 膨胀泊松分布参数的估计结果和0-2 膨胀泊松分布参数的估计结果.于0-1 膨胀泊松分布而言,0 膨胀参数的估计值为0.417 2,1 膨胀参数的估计值为0.619 9,泊松部分的参数估计值为2.632 8,经过计算得到该分布的数学期望为1.693 0;于0-2 膨胀泊松分布而言,0 膨胀参数的估计值为0.336 9,2 膨胀参数的估计值为0.714 8,泊松部分的参数估计值为2.408 2,经过计算得到该分布的数学期望为1.789 0.从样本数据来看,ART的平均值为1.692 9(或称为真实值),基于0-1 膨胀泊松分布计算的数学期望与真实值十分接近,相对误差在±0.01%之内;基于0-2 膨胀泊松分布计算的数学期望与真实值的相对误差为5.68%,说明0-2 膨胀泊松分布会高估原始数据的均值.由此可见,采用0-1 膨胀泊松回归模型进行建模分析会更加可靠.

表3 0-1 膨胀泊松分布的参数估计结果Tab.3 0-1 Parameter estimation results of expansion Poisson distribution

表4 0-2 膨胀泊松分布的参数估计结果Tab.4 0-2 Parameter estimation results of expansion Poisson distribution
从统计检验的角度而言,表5 和表6 分别给出了0-1 膨胀泊松分布是否会退化和0-2 膨胀泊松分布是否会退化的检验结果.通过查表可得自由度为2、置信水平为0.05 的卡方分布临界值是5.99.从表5来看,Wald统计量与LR统计量均拒绝了退化为0 膨胀泊松分布、退化为1 膨胀泊松分布以及退化为非膨胀的泊松分布的原假设,说明原始数据存在0-1 膨胀现象,可以采用0-1 膨胀泊松回归模型进行建模分析.从表6 来看,Wald统计量均拒绝了退化为0 膨胀泊松分布、退化为1 膨胀泊松分布以及退化为非膨胀的泊松分布的原假设,而LR统计量仅拒绝了退化为2 膨胀泊松分布和退化为非膨胀的泊松分布的原假设,但并未拒绝退化为0 膨胀泊松分布的原假设,说明从LR检验来看0-2 膨胀泊松分布会退化为0 膨胀泊松分布,这意味着原始数据不存在2 膨胀的现象,因此不应该采用0-2 膨胀泊松回归模型进行建模分析.综上所述,对于样本数据更适合建立0-1 膨胀泊松回归模型而非0-2 膨胀泊松回归模型,这一结论与前文所述的“0-2 膨胀泊松分布会高估原始数据均值”相互佐证.

表5 0-1 膨胀泊松分布的膨胀参数检验结果Tab.5 0-1 Expansion parameter test results of Poisson distribution of expansion

表6 0-2 膨胀泊松分布的膨胀参数检验结果Tab.6 0-1 Expansion parameter test results of Poisson distribution of expansion
5 结语
本研究通过引入隐变量设定0-k膨胀回归模型,采用EM算法给出了各个参数的点估计值并基于Fisher 信息矩阵构造了置信区间;对0-k膨胀分布是否会退化的现象进行假设检验,通过Wald统计量和LR统计量给出了检验方法;以0-k膨胀泊松回归模型为例进行实际应用,包括回归系数的估计、分布参数的估计以及膨胀参数的统计检验.由此得到以下主要结论:采用EM 算法对参数进行点估计时,回归系数与膨胀参数估计值的迭代收敛速度较快并且估计结果稳健;基于Fisher 信息矩阵给出了0-k膨胀回归模型的区间估计结果,为参数的置信区间构造提供了一种思路;于0-k 膨胀泊松分布而言,当k取不同值时可能会对原始数据的拟合出现偏差,在统计检验时发现LR 统计量的检验效果要优于Wald统计量的检验效果.

