Optimal and robust control of population transfer in asymmetric quantum-dot molecules

Yu Guo(郭裕), Songshan Ma(马松山), and Chuan-Cun Shu(束传存)

1Hunan Provincial Key Laboratory of Flexible Electronic Materials Genome Engineering,School of Physics and Electronic Science,Changsha University of Science and Technology,Changsha 410114,China

2Hunan Key Laboratory of Nanophotonics and Devices,School of Physics,Central South University,Changsha 410083,China

Keywords: population transfer,quantum optimal control theory,quantum-dot molecules

1.Introduction

Population transfer is a fundamental concept in various domains of quantum physics, including quantum information processing, quantum computing, and quantum optics.[1–5]Its primary objective is manipulating a quantum system from its initial state to a desired target state, which can be achieved by applying external control fields,such as laser pulses,electromagnetic fields,or magnetic fields.By carefully designing these control fields, it becomes possible to efficiently control the dynamics of the quantum system, ultimately enabling the transfer of population between different states.[6–12]

Several coherent quantum control techniques have been widely used to achieve population transfer, such as stimulated Raman adiabatic passage (STIRAP),[13,14]shortcuts to adiabaticity,[15–17]and composite pulses.[18,19]By formulating the population transfer problem within an optimal control framework, quantum optimal control theory offers a powerful tool for finding optimal control strategies that maximize transfer efficiency while including constraints on the control fields.[20–29]In practical applications,it is vital to develop robust quantum control strategies that account for uncertainties and disturbances arising from fluctuations in control field parameters or environmental noise sources.However, ensuring the effectiveness and reliability of population transfer in quantum systems remains challenging,as it requires designing optimal control fields capable of overcoming such uncertainties.

To demonstrate robust optimal control,we take the semiconductor quantum dots (SQDs) as an example, which possess discrete energy levels,high nonlinear optical susceptibility,and exceptional controllability and adjustability.[30–34]By arranging two or more coupled quantum dots separated by a tunnel barrier,a fascinating system known as a“quantum-dot molecule” can be formed, showcasing molecular-like structures and captivating quantum phenomena arising from the coherent tunneling of charge carriers between the individual quantum dots.These phenomena can be effectively harnessed for various practical applications.[35–43]We concentrate on achieving optimal and robust population transfer in an asymmetric double quantum-dot molecule (ADQDM).[44–48]The present system consists of two SQDs with distinct band structures connected through tunneling.Extensive research has been conducted on such systems, revealing intriguing optical phenomena such as tunneling-induced transparency,[49–51]tunneling-induced optical limiting,[52]tunneling-induced Talbot effect,[53]and tunneling-induced phase grating.[54–56]

In this work, we show how to apply analytical methods[57–60]for achieving optimal control of population transfer by manipulating the spectral amplitude of a narrow bandwidth pulse.However, this method suffers from long pulse durations and high sensitivity to control field parameter fluctuations.To overcome these limitations, we utilize a frequency domain quantum optimal control theory (FDQOCT)method[27–29]to find optimal control fields in the broad bandwidth regime.Unlike time-domain methods[24]that shape the temporal field directly, FDQOCT optimizes complex spectral fields in the frequency domain.By optimizing the spectral phase while preserving the spectral amplitude,we can achieve spectral-phase-only optimization, reducing the search space,conserving laser energy,and emphasizing quantum coherence effects.Our results demonstrate efficient population transfer to the target state while suppressing undesired state populations,even in the presence of fluctuations in control field parameters.This work presents a valuable approach for finding robust optimal control schemes to mitigate uncertainties and fluctuations in practical applications.

The paper is organized as follows.In Section 2,we briefly describe the model and the solution approach for the asymmetric double quantum-dot molecule,and the overview of the FDQOCT algorithm employed.In Section 3, we present numerical simulations and discussions on the population transfer in two distinct regions: narrow bandwidth and broad bandwidth of the laser pulse.Finally,we conclude our findings in Section 4.

2.Theoretical model and optimization methods

We consider an ADQDM composed of two single SQDs:the left SQD and the right SQD.These two SQDs have different band structures and are connected through electron tunneling.ADQDMs can be fabricated using self-assembled dot growth technology.For example, they can be grown on GaAs(001) substrates utilizing molecular beam epitaxy and precise atomic layer etching techniques.[45]As shown in Fig.1(a), this system consists of three levels denoted by|1〉,|2〉,and|3〉.The ground state|1〉defines a level in which two SQDs are not excited.The direct exciton state|2〉 stands for the level at which an electron is excited to the conduction band in the left SQD to form an electron–hole pair,and the indirect exciton state|3〉has one hole in the left SQD and one electron in the right SQD.[44]A laser pulseℰ(t)is introduced to couple the ground state|1〉and the direct exciton state|2〉,which can be further coupled with the indirect exciton state|3〉 through electron tunneling.

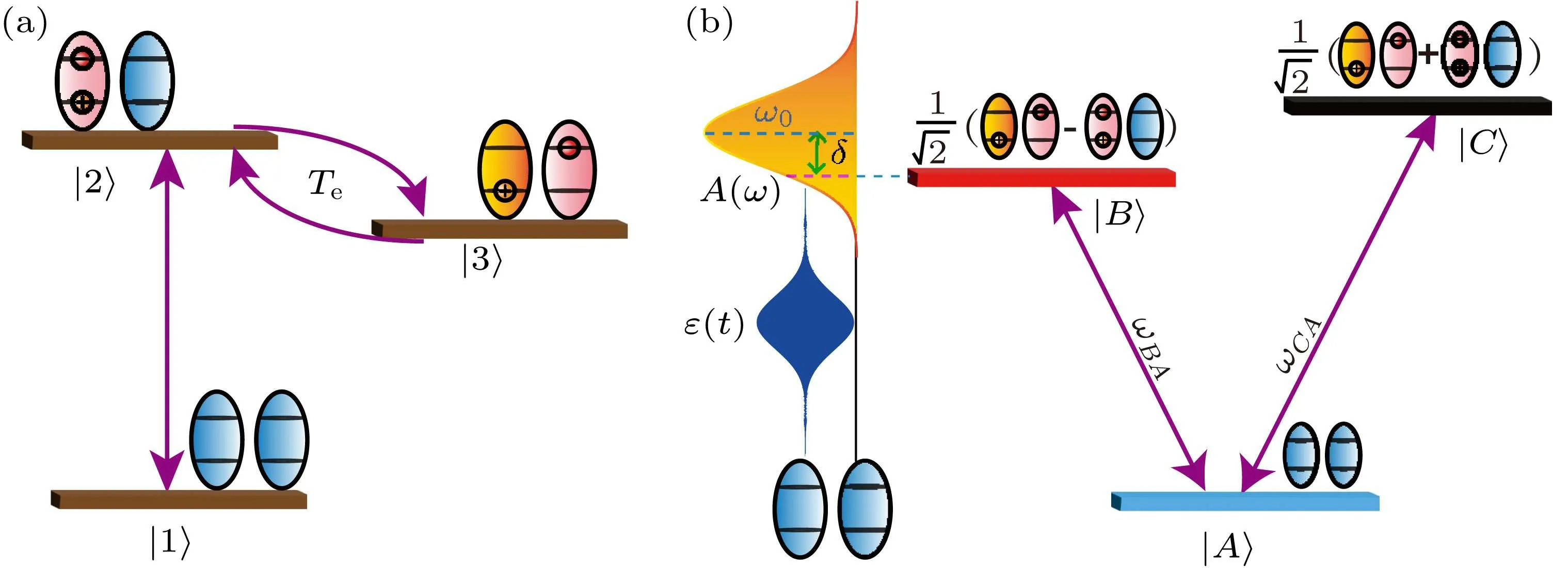
Fig.1.Schematic illustration of energy level configuration of the asymmetric double quantum-dot molecule in (a) the bare energy basis(|1〉,|2〉,and|3〉),and(b)the dressed energy basis(|A〉,|B〉,and|C〉).

The total time-dependent Hamiltonian can be written asH(t)=H0+Hint(t) (¯h=1) in the energy basis (|1〉,|2〉,|3〉)with

with the corresponding eigenvaluesωA=E1,ωB=E2-Te,andωC=E3+Te,considering the degeneracy of the two exciton states.In the above basis, the total HamiltonianH(t)can be expressed as

in terms of a complex functionΩ(ω)in the frequency domain,whereΩ(ω)=A(ω)exp[iφ(ω)]is a product of a spectral amplitudeA(ω)and a spectral phaseφ(ω).In this work,we explore how to find optimal time-dependent control fields [i.e.,Ω(t)]by analytical designing the spectral amplitudeA(ω)in Subsection 2.1 and by optimizing the spctral phaseφ(ω) in Subsection 2.2.

2.1.Population transfer by controlling the spectral amplitude

To obtain an analytical solution,we transform the Hamiltonian given in Eq.(4) into the interaction picture without utilizing the rotating-wave approximation.The transformed Hamiltonian,denoted asHdI(t),is expressed as

whereωij=ωj-ωirepresents the frequency difference between states|i〉and|j〉,withi,j=A,B,C.

To achieve high-efficiency population transfer from|A〉to|B〉 or|C〉, we can derive an analytical time-dependent wave function for the V-type three-level system.The system is coupled with a time-dependent couplingΩ(t),which is turned on at the initial timet0and turned off at the end timetf.The time-dependent unitary operatorU(t,t0)of the system can be expanded using the Magnus expansion.[61–64]Considering the first leading termU(1)(t,t0)=exp[-it t0dt′HdI(t′)], the timedependent wave function of the system can be given by

wherek ∈N, and the final timetfcorresponds to the instant when the coupling is switched off.

By performing the frequency-domain analysis,we can design the time-dependent coupling’s spectral amplitudeA(ω)to achieve these desired pulse area values.Specifically,we adopt a Gaussian-frequency distribution for the spectral amplitude by with the pulse durationτ0=1/∆ω.By controlling these parameters withA0=|θB/C(tf)| andω0=ωB/CA, and choosing∆ωnarrow enough,we can achieve efficient population transfer from|A〉to|B〉or|C〉at the final timetf.

2.2.Population transfer by optimizing the spectral phase

The above-mentioned control scheme revolves around manipulating the spectral amplitude, which requires control fields characterized by long pulse durations and precise control parameters.As a result, the efficiency of the control scheme is greatly impacted by fluctuations in the control field parameters and decoherence arising from the surrounding environment.[48]To tackle these challenges, we use the FDQOCT method developed in Refs.[27–29] to determine optimal time-dependent control fields by optimizing the spectral phase while keeping the spectral amplitude unchanged.This approach,utilizing spectral phase-only optimization,offers several advantages.Firstly, it reduces the search space,leading to more efficient optimization.Secondly,it highlights the impact of the spectral phase in quantum control.Importantly, this method maintains the laser energy input without making any alterations.

To employ the FDQOCT method,a dummy variables ≥0 is used to track the changes of the spectral phaseφ(s,ω)from an initial guessφ(si,ω)to the optimized oneφ(sf,ω)and the corresponding variation of cost functional,which is the populationPB/C(s,tf)of the target state|B〉or|C〉at the final timetf.The objective is to increase the value ofPB/C(s,tf)by updating the spectral phase fromφ(s,ω)toφ(s+δs,ω),which can be formulated as

A normalized Gaussian functionS(ω′-ω) =exp[-4ln2(ω′-ω)2/σ2] is introduced as a convolution filtering method to locally average the inputsδQℓ/δφ(s,ω) by choosing an appropriate value for the parameterσ.

3.Results and discussion

3.1.Numerical simulations for the first approach

To examine the first approach, we employ the analytically designed pulse as described in Eq.(10),withω0=ωBA,to achieve population transfer from state|A〉 to state|B〉.In our simulations, we take parametersE1=0.1 eV,E2=E3=0.4 eV,andTe=0.5 meV.Figure 2 demonstrates the final populations of the target statePBand the undesired statePCas functions of the amplitudeA0(i.e., the pulse areaθB)and the frequency bandwidth ∆ω.For the sake of simplicity,we defineθB/C ≡θB/C(tf) andPB/C ≡PB/C(tf).The results indicate efficient population transfer to state|B〉can be achieved when the pulse bandwidth is sufficiently narrow.Interestingly, amplitudes ofA0=π/2 or 3π/2 lead to high-efficiency population transfer to the target state|B〉,in line with the pulse-area conditions in Eq.(8).Specifically,when ∆ω=0.01Te,the transfer efficiencyPBcan reach a value of 0.999 while effectively suppressing the population of state|C〉withPC(t)<10-5.However, it is worth noting that in the case of a broad bandwidth regime,the excitation to state|C〉also becomes significant due toθC ̸=0 in Figs.2(c)and 2(d).

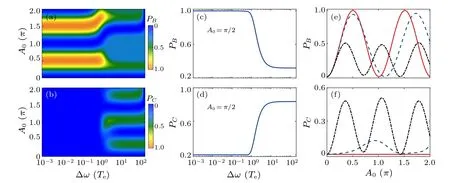
Fig.2.[(a),(b)]The dependence of the final populations PB and PC on both the amplitude A0 and the frequency bandwidth ∆ω by using Gaussian pulses with the central frequency ω0 =ωBA.[(c), (d)] PB and PC as functions of ∆ω with A0 =π/2.[(e), (f)] PB and PC as functions of A0 with the bandwidths ∆ω=0.01 Te(red solid line),∆ω=1.0 Te(blue dashed line),∆ω=10 Te(black dotted-dashed line).

To better understand the impact of bandwidth ∆ω,Figs.2(e)and 2(f)plot the cut lines ofPBandPCas functions ofA0for three bandwidths:∆ω=0.01Te(narrow bandwidth),∆ω=1.0Te,and ∆ω=10Te(broad bandwidth).In the case of broad bandwidth,it is evident that the Rabi oscillations are incomplete,and the maximum population of the oscillation decreases as ∆ωincreases until it reaches a fixed value.This implies that the pulse-area conditions cannot be satisfied with broad bandwidth.However,a complete Rabi oscillation can be observed in the case of narrow bandwidth.The transfer to the target state occurs atA0=π/2+kπ(k ∈N),where the pulse area is precisely satisfied.Furthermore,the central frequencyω0exactly resonates with the transition frequencyωBA.

3.2.Numerical simulations for the second approach

We now explore the second approach,which involves utilizing the FDQOCT method to search for optimized spectral pulses in the broad bandwidth regime.In particular, we select a broad bandwidth of ∆ω=10Teas an example for our simulations.We initialize the input with a zero spectral phase,φ(si,ω)=0.Additionally,we set the filtering function with a bandwidth ofσ=0.15 eV andω0=ωBA.To obtain generalized results,we conduct the FDQOCT simulations for various values of the amplitudeA0,scanning it from 0 to 2π.We employ the FDQOCT algorithm throughout the optimization process to optimize the spectral phase while keeping the spectral amplitude atA0.

Fig.3.The optimal simulations for the frequency bandwidth ∆ω =10 Te.(a)The cost functional as a function of the amplitude A0.(b)The corresponding optimized spectral phases.The optimization process is terminated when the objective value is converged to 0.999.

Figure 3 shows the cost functional,i.e.,the final optimal populationPB, and the corresponding optimal spectral phases as functions of the amplitudeA0.To facilitate readability,we perform an overall phase shift to attain a minimum value of 0 and then modulate the phases to ensure it falls within the[0,2π] range in Fig.3(b).It is observed that the FDQOCT method can find optimal control pulses capable of achieving high-efficient population transfer,withPB>0.999,as long as the amplitudeA0exceeds a certain thresholdA0≥0.61π.

In the following analysis,we examine the results forA0=πas an example to investigate the optimized control pulses further.Figure 4 illustrates the optimized control pulse and the corresponding time-dependent populations in three states.Specifically,as a comparison,Fig.4(a)depicts the fixed spectral amplitudeA(ω), described by Eq.(9) with ∆ω=10Te,and the initial spectral phaseφ(si,ω), which are used in the FDQOCT simulation.The corresponding initial temporal control pulse is shown in Fig.4(b).Figure 4(c) shows the population evolution of the three states driven by the initial control pulse.Due to the broad bandwidth,the initial pulse with a flat spectral phase,i.e.,φ(si,ω)=0,leads to a notable population transfer to the undesired state|C〉.

Figure 4(d) plots the optimized spectral phase achieved through the FDQOCT optimization.To obtain the optimized temporal pulse, we incorporate the fixed spectral amplitudeA(ω) and the optimized spectral phaseφ(sf,ω) into the inverse Fourier transform,as expressed by Eq.(5).The resulting optimized temporal pulse is shown in Fig.4(e).Compared to the initial pulse,the optimized spectral phase reduces the peak intensity of the optimized temporal pulse while significantly extending its duration.However, it is important to note that the time duration remains much shorter than that of the narrow bandwidth pulse with ∆ω ≪1.0Te.Figure 4(f)shows the corresponding dynamical evolution of the populations in the three states achieved using the optimized control pulse.Although the spectral amplitude is kept unchanged as the initial one, the optimized time-dependent pulse via the spectralphase-only optimization maximizes the population transfer to the target state|B〉while significantly suppressing its transfer to the undesired state|C〉.

We finally analyze to assess the impact of experimental errors on the population transfer driven by the optimized control fields.Specifically,we focus on errors resulting from variations in the amplitude and central frequency of the control fields.

Figure 5(a) depicts the dependence of the final populationPBon the control field’s amplitudeA0and the detuningδ=ω0-ωBA.The final population in the target statePBconsistently remains above 0.999 across a wide range of parameter values.This observation underscores the robustness of the population transfer process against experimental errors,highlighting the reliability of the optimized control fields.To further explore the effect of the pulse amplitude variation,we plot the corresponding cut lines ofPBas a function of the pulse amplitudeA0withδ=0 in Fig.5(b).The results demonstrate a monotonic increase in transfer probability with an increasing pulse amplitude(A0).Notably,when the value ofA0exceeds 0.8π,the transfer probability consistently exceeds 0.999.Additionally, we investigate the impact of variations in central frequency by plotting the cut lines ofPBagainst detuning(δ),with the amplitude fixed atA0=π,as shown in Fig.5(c).The population transfer ofPBgreater than 0.999 can be achieved when detuning varies within the range of[-1.2,3.9]meV.

In addition, we also perform similar simulations for achieving reliable and efficient population transfer to the symmetric delocalized state|C〉, not presented here.It is worth noting that the results of the robustness of the population transfer process remain consistent across these simulations.This further emphasizes the robustness and effectiveness of the optimized control fields, even in the presence of experimental errors resulting from variations in pulse intensity and central frequency.

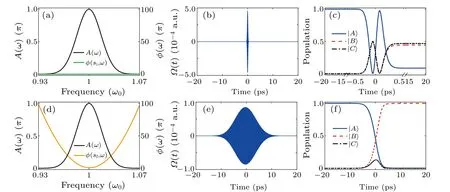
Fig.4.FDQOCT simulation results with the initial and optimal spectral fields for A0=π and the frequency bandwidth ∆ω =10 Te:(a)the fixed spectral amplitude A(ω)and the initial spectral phase φ(si,ω),[(b),(c)]the corresponding time-dependent control pulse and population evolutions in three states,[(d)–(f)]the same as(a)–(c)with the optimized spectral phase φ(sf,ω).

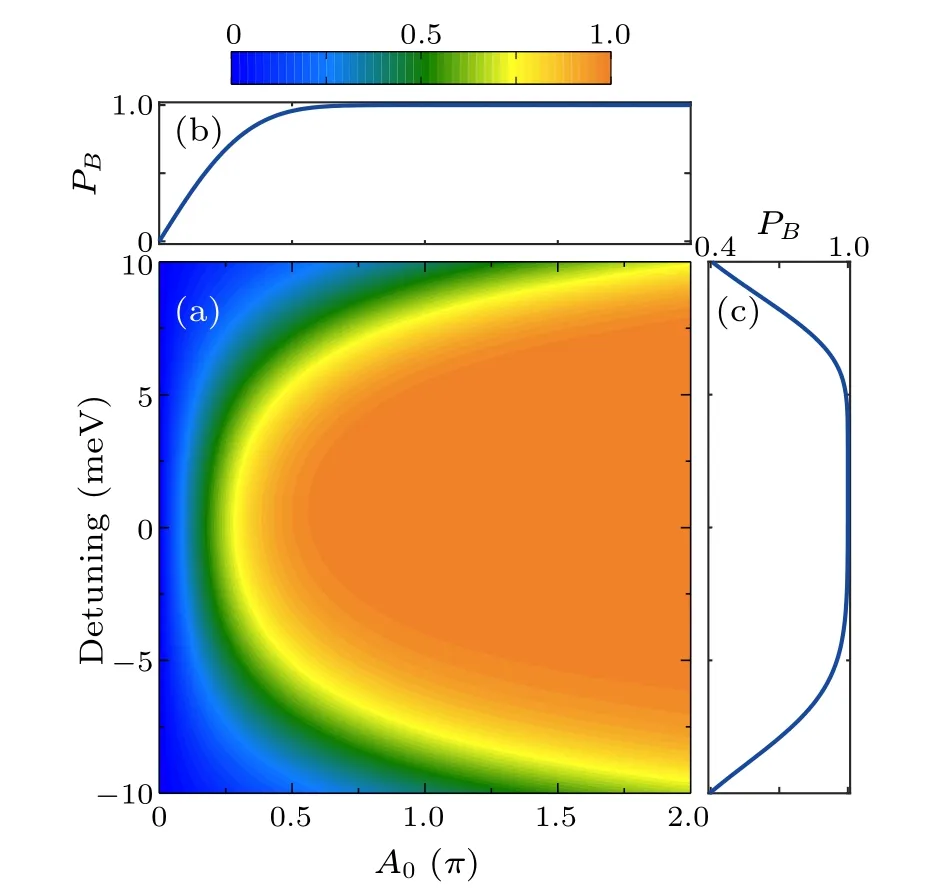
Fig.5.The robustness of population transfer to the target state |B〉 by using the optimized control pulse: (a) final population PB versus the amplitude A0 and the detuning of the optimized control field, and the corresponding cut lines at(b)δ =0 and(c)A0=π.

4.Conclusion

In summary, we have presented an implementation of population transfer in the ADQDM, explicitly targeting the transfer from the ground state to the delocalized states.These delocalized states correspond to the maximal coherent superposition states between the direct and indirect exciton states.In the case of narrow bandwidth,we utilize a control pulse that satisfies the pulse-area conditions, leading to complete population transfer from the ground state to the desired target state.On the other hand,when dealing with a broad bandwidth,we employ the FDQOCT method to search for the optimal spectral phase while maintaining a fixed spectral amplitude in the frequency domain.The resulting optimized control pulse enables high-efficiency population transfer to the desired state while exhibiting robustness against variations in both the pulse amplitude and central frequency.Our work offers a valuable strategy for achieving population transfer in the ADQDM system and holds significant potential for applications in quantum information processing.

Acknowledgments

This work was supported by the National Natural Science Foundations of China(Grant Nos.12275033,61973317,and 12274470), the Natural Science Foundation of Hunan Province for Distinguished Young Scholars (Grant No.2022JJ10070), the Natural Science Foundation of Hunan Province (Grant No.2022JJ30582), and the Scientific Research Fund of Hunan Provincial Education Department(Grant No.20A025).