Chiral bound states in a staggered array of coupled resonators

Wu-Lin Jin(金伍林), Jing Li(李静), Jing Lu(卢竞), Zhi-Rui Gong(龚志瑞), and Lan Zhou(周兰),†

1Synergetic Innovation Center for Quantum Effects and Applications,Key Laboratory for Matter Microstructure and Function of Hunan Province,Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of the Ministry of Education,Synergetic Innovation Center for Quantum Effects and Applications,Institute of Interdisciplinary Studies,Xiangjiang-Laboratory and Department of Physics,Hunan Normal University,Changsha 410081,China

2College of Physics and Optoelectronic Engineering,Shenzhen University,Shenzhen 518060,China

Keywords: bound states,two-level small atom,coupled-resonator array,chirality

1.Introduction

One typical arrangement of CRAs is a quantum emitter coupling via Jaynes–Cummings-type interaction to only one resonator of the CRA with identical physical properties of resonators and uniform-hopping rates.[12–14]In the singleexcitation sector,this single-atom CRA supports unbound stationary states with energies forming a cosine-shaped band,and two localized atom-photon bound states with energies slightly outside the continuum,[5,15]where each bound state is localized and symmetrical around the resonator coupling to the quantum emitter.The dynamics of the excitation in this singleatom CRA shows that the formation of atom–photon bound states results in the partial field localization and atomic population trapping.[16,17]The non-local coupling of the quantum emitter to the CRA with the cosine-shaped band has been studied,[18,19]bound states with energies outside the band are also been found.

In this work,we study a system in which a two-level small atom is coupled to adjacent resonators in a one-dimensional(1D) CRA with staggered hopping strengths (referring to a staggered CRA for short) via electric dipoles.It is different from the system of a two-level giant atom non-locally couples to two non-adjacent resonators in the Su–Schrieffer–Heeger(SSH) chain in Ref.[20].More importantly, this system is simple to implement.In the absence of the two-level small atom, the staggered CRA forms two propagating bands with nonlinear dispersion without bound states, which is different from the system of a staggered CRA with finite length.[21–28]Those propagating bands are the complete basis of the Hilbert space of the photon which apparently possess the finite probability to appear at the large distance.When the two-level small atom is introduced, the bound state can be regarded as a linear combination of those propagating bands.In this sense,the localization of the photon around the two-level small atom is considered as the coherence creation of the propagating bands in the vicinity of the two-level small atom and the simultaneous coherence destruction of the propagating bands at large distance.Hence the bound states emerge in such system.It is natural to ask the following questions: How many bound states in a staggered CRA? Do they still have the reflection symmetry around the resonator that the two-level small atom is coupled to? If mirror symmetry is broken,how to measure and adjust this asymmetry? To find the answers to these questions, we study both local and non-local coupling of a twolevel small atom to the staggered CRA.The local coupling means that the two-level small atom only interacts with one resonator.For non-local coupling, we only consider the twolevel small atom only interacts with two adjacent resonators.

The paper is organized as follows.In Section 2,we propose the model describing the interaction between a staggered array of coupled resonators and a two-level small atom, and the equations of the probability amplitudes are presented in single-excitation subspace.In Section 3, we derive the condition for the single-photon bound states when two bands are presented, then introduce chirality to measure the mirror asymmetry of the bound states,achieve the control of the chirality of the bound states when the two-level small atom is locally or non-locally coupled to the staggered array and conduct an in-depth analysis of the directionality of chirality and the physical mechanisms.Finally,a summary has been made.

2.Model for a two-level small atom non-locally coupled to a staggered array

The model system we proposed is depicted schematically in Fig.1.A 1D array of identical, single-mode resonators is coupled to an individual two-level small atom.Each resonator is modeled as a single harmonic oscillator mode of frequencyω.Nearest-neighbor resonators are coupled with staggered hopping energies where the two possible hopping energiest+δandt-δare interspersed along the array.The staggered CRA can be realized by circuit QED,that is,an array of coupled inductor–capacitor (LC) resonators is utilized to simulate the staggered CRA,and the coupling strength between LC resonators is controlled by capacitance and mutual inductance.[21,22]We cast the array into a tight-binding chain of equally-spaced sites with staggered hopping strength,which seems similar to the Peierls distorted chain, but the chain is assumed to be infinitely long in both direction.The free Hamiltonian of the staggered CRA reads

where the bosonic ladder operator ˆaj(ˆbj)annihilate a photon at thea(b) resonator of thej-th unit cell marked by rectangles in Fig.1.t+δis the intracell hopping andt-δis the intercell hopping.The first term in Eq.(1)is the on-site contribution, the other terms are responsible for the tunneling of photons between adjacent resonator.Forδ=0, we retrieve the CRA with uniform hopping energy usually considered in the studies of single-photon transport.[5–9,12–14,16–19,29–32]The Fourier transform and some algebra reveal that the staggered CRA support Bloch bands and Bloch waves with the dispersion relation

wherekis the momentum along the staggered CRA.The energy spectrum of the staggered CRA is two separate bands,the width of each band is 2(t-δ)and the band gap is 4δ.

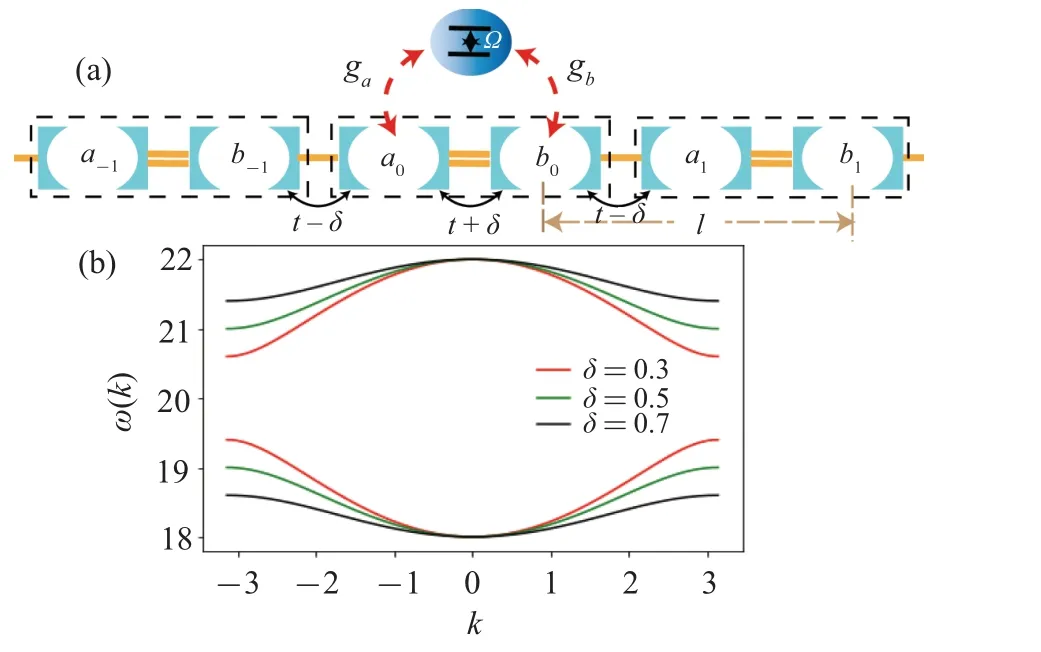
Fig.1.(a)Schematic depiction of a two-level small atom non-local coupled to the nearest resonators in a staggered array made of coupled resonators.Dashed boxes indicate the unit cells.(b)The dispersion relation of the dimer chain for δ ̸=0.All parameters are in units of the hop strength t.

The excited state|e〉and ground state|g〉of the two-level small atom are separated by the Bohr frequencyΩ, and their transition is electric-dipole coupling to the mode of the adjacent resonators at the 0-th cell.Under the rotating-wave approximation the Hamiltonian of the bare two-level small atom and the transfer of excitations between the two-level small atom and field in the staggered CRA are described by

在吴健雄的手札中，也可以看出这种情愫的暗中涌动：“刚在电话中替您道别回来，心想您明天又要‘黎明即起’地去赶路，要是我能在晨光曦微中独自驾车到机场去替您送行多好，但是我知道我不能那样做，只能在此默祝您一路平安。”她想亲自驾车为他送行，可是不能那样做，她是理智的女人，只能压抑自己的感情，在心底默默想念他。

whereσzis thezcomponent of the Pauli matrices which acts on the two internal states|e〉and|g〉andσ-(σ+)is its corresponding lowering(raising)operator.The non-local coupling between the two-level small atom and the staggered CRA can be realized by capacitors, and the coupling strengths can be adjusted by capacitors.[34]

The operator ˆN= ∑j(ˆa†jˆaj+ ˆb†jˆbj)+|e〉〈e| commutes with the total HamiltonianH=H0+H1of the system,which features a fixed number of excitations.The eigenstates of the HamiltonianHcan be constructed by the eigenstates of the conserved quantity ˆNwith the ansatz

where ˆa†j|/0〉 (ˆb†j|/0〉) denotes a single photon occupying the mode of thea(b) resonator at thej-th unit cell, and ˆσ+|/0〉stands for the two-level small atom excited state.Substituting the ansatz in stationary Schrödinger equation leads to a set of relations for the coefficientsαjandβj

When one of the coupling strengthgn= 0, we retrieve the model where the two-level small atom interacts with only one resonator of the staggered array,i.e.,the two-level small atom is locally coupled to the staggered array.

3.Single-photon bound states

In the absence of the two-level small atom, the staggered CRA exhibits two continuous spectrums of propagating waves.The presence of the two-level small atom breaks down the translation symmetry of the staggered array, so the nonpropagating eigenstates are formed, which are called the bound states (BSs).The bound states are dressed atom-field eigenstates localized around the quantum emitter.[5,6,8,9,17,19,32]In Fig.2,we plot the eigen-energy in the single excitation subspace by numerically diagonalising the Hamiltonian in the real space.In general, it can be found that there are three bound states: one lies above all bands(called BS I),one lies within the band gap(called BS II),and one lies below all bands (called BS III).Nevertheless, whenga=gb=gthe number of bound states can be controlled by adjustinggandδ, so that there is one, two or three bound states.

Since bound states are waves that remain localized, we assume the following solutions to Eq.(6)withk0=0,π

which decay exponentially with the distance from the site that the two-level small atom is coupled to, whereΘ(j)=1 forj>0 andΘ(j)=0 forj<0.The relation of the imaginary wave vectorκ>0 and the energy of a localized photon outside of the bands is obtained as

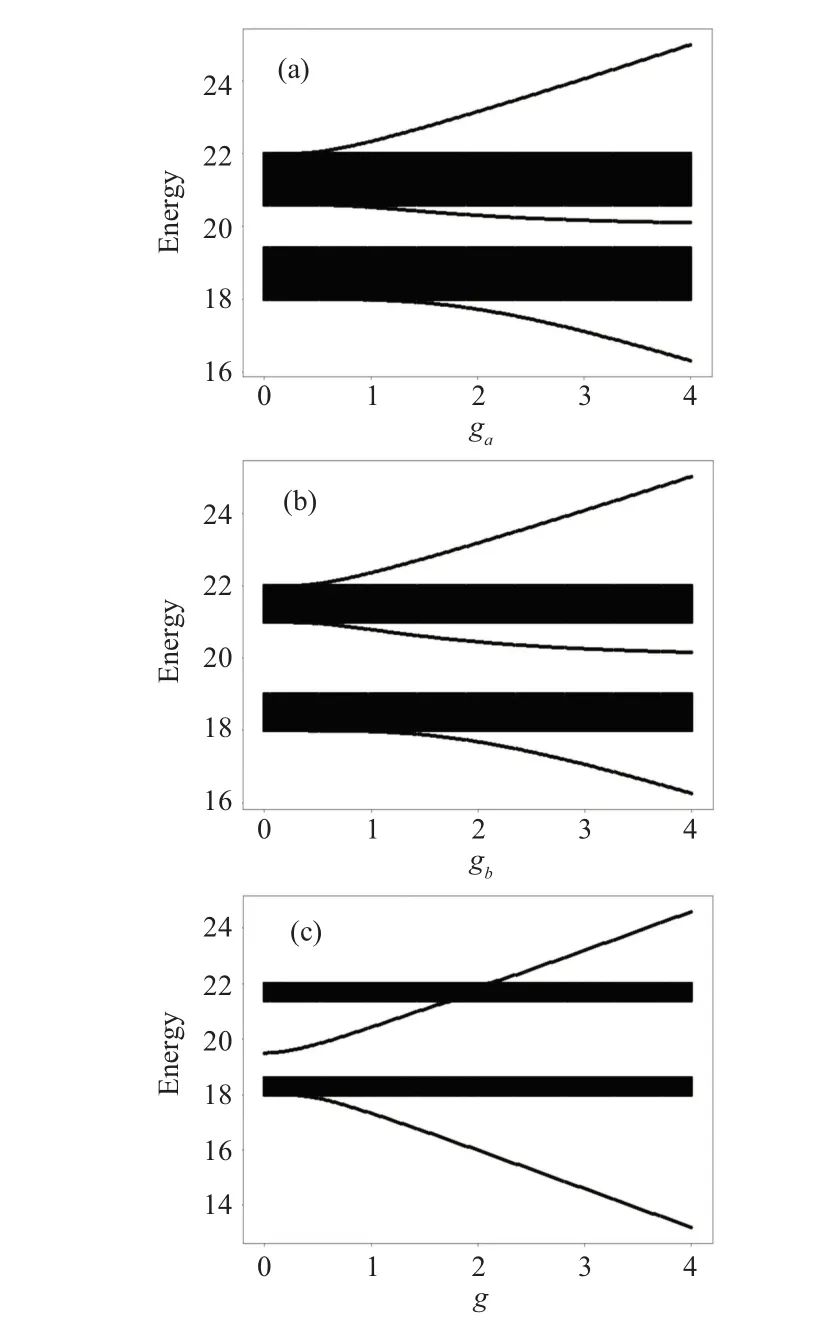
Fig.2.The spectrum as a function of the coupling strength with ω =20.(a)Ω =21.5,δ =0.3,gb=0;(b)Ω =21.5,δ =0.5,ga=0;(c)Ω =19.5,δ =0.7,ga=gb=g.All parameters are in units of the hop strength t.

Applying Eqs.(9)and(11)to the discrete scattering equation(6)atj=±1,the amplitudes for thej=0 cell read

The number of the bound states completely determined by the above conditions.

3.1.Local coupling

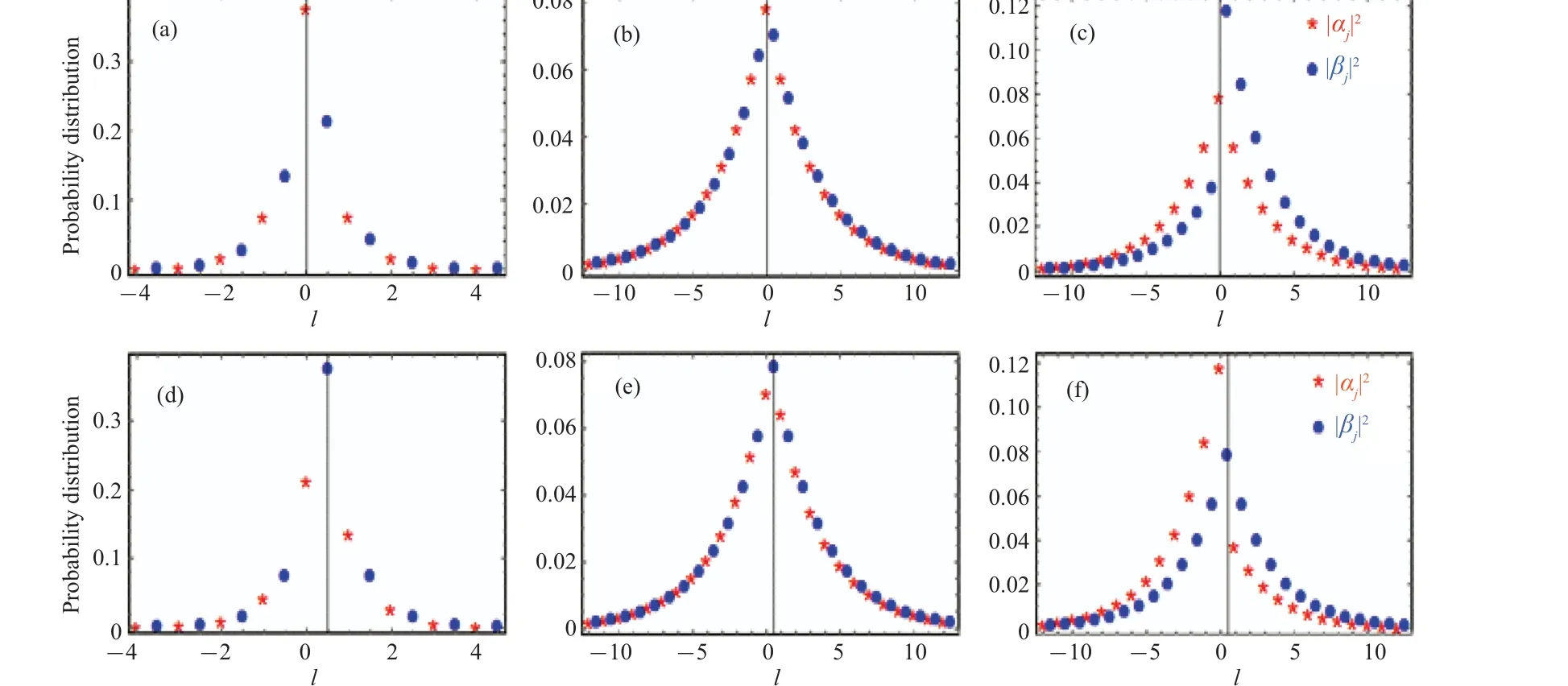
Fig.3.The probability distribution of the bound state I (panels (a) and (d)), III (panels (b) and (e)), and II (panels (c) and (f)).The two-level small atom is coupled only to the a0 resonator in the upper panels(panels(a)–(c)).The two-level small atom is coupled only to the b0 resonator in lower panels(panels(d)–(f)).All parameters are in units of the hop strength t and ω =20,Ω =21.5,δ =0.3.

In Fig.3, we have plotted the probability distribution of the bound state I(panels(a)and(d)), III(panels(b)and(e)),and II(panels(c)and(f))whenga=0.7,gb=0(panels(a)–(c))orga=0,gb=0.7(panels(d)–(f))respectively.The black line located at origin in each upper panel and coordinatel/2 in each lower panel is the line of symmetry.It can be observed that: (i) The red stars (blue dots) distribute symmetrically around the black line in each upper (lower) panel.(ii)All the bound states prefer to localize at the right side of the two-level small atom forgb=0,andvice versaforga=0.(iii)Panels(d),(e),and(f)appear as the reflection of the panels(a),(b),and(c)followed by a shift to the right byl/2 distance,respectively.So in the following,we focus our discussion on the case withgb=0.

To further quantify the mirror symmetry of bound states,we introduce the chirality[34]whereS>0(S<0)indicates that the chirality prefers the left(right)direction, andS →1(S →-1)corresponds to perfect left(right)chirality.The chirality can be further expressed as

with the help of wave function in Eq.(9).To present how to tune the chirality of these bound states,we plot the chiralitySas a function ofδin Fig.4 with different Bohr frequencyΩfor fixed coupling strength.

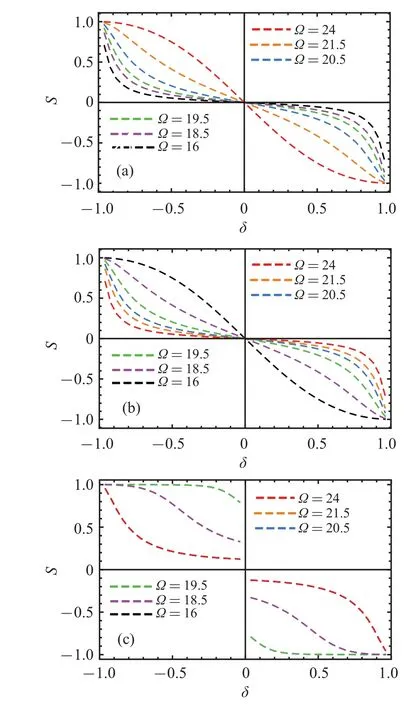
Fig.4.The chirality of the bound state I(a),III(b),and II(c)versus δ for local coupling.Here, ω =20, ga =0.7.All parameters are in units of the hop strength t.

It can be found that(i)one can continuously tune the chirality of bound states I and III over the whole rangeδ ∈[-1,1],so does the chirality of bound state II as long as the hopping strengths are staggered.In particular,whenδ →0,the chirality of bound states I and III tends to 0,however the chirality of bound state II is far from 0.Without the staggering,i.e.,δ=0 the staggered array becomes a uniform array,and bound state II disappears.The chirality of bound state II is discontinuous at(0-,0+), which corresponds to the closure and opening of the band of the staggered CRA,and also to the different topology of the staggered CRA for positive or negativeδ.(ii)The chirality prefers left direction whenδ<0 and prefers right direction whenδ>0,i.e.,the photon would like to appear at the left side of the line of the symmetry whenδ<0 and at the right side whenδ>0.The underlying mechanism is the following:the two-level small atom creates a single photon into the mode of thea0resonator, from where the photon can hop to other resonator.Single photon hop to the side where the hopping strength is larger, hence, the hopping strength determines the chiral.The discontinunity of the chirality of the bound state II actually relates to the topology of the staggered CRA, whereδ<0 andδ>0 corresponds to opposite widing number.(iii)The left (right) chirality increases asΩincreases for bound state I and decreases asΩincreases for bound state III.However, the chirality of the bound state II increases as the Bohr frequencyΩis closer to the resonator’s frequencyω.Whenδ=±1, the staggered CRA falls apart to a sequence of disconnected dimers.The energy of the dimer which couples to the two-level small atom is different from the energiesω±2tof other dimers,whose eigenstates are the even and odd superpositions of the two sites forming a dimer.A single photon is completely localized at the dimer the two-level small atom is coupled.Hence,the chirality is completely determined by the site which is close to thea0resonator,i.e.,the amplitudeβ0orβ-1.

3.2.Non-local coupling

We now consider the case that all coupling strengthgn ̸=0.We assume that the two-level small atom is located at the middle of the unit cell atj=0,so,the line of symmetry is located at coordinatel/4.The probabilities at the right and left side of the line become

With the help of Eq.(12),we obtainS=0,which can be understood easily because the system has mirror symmetry around the line passing through coordinatel/4.This result told us that chirality may arise whenga ̸=gb.In Fig.5, we plot the chiralitySof the bound state versusδ.

Fig.5.The chirality of the bound state I (panels (a) and (d)), III (panels (b) and (e)), and II (panels (c) and (f)) versus δ for non-local coupling.Here,ga=0.7,gb=0.6 for upper panels and ga=0.6,gb=0.7 for lower panels.All parameters are in units of the hop strength t and ω =20.

It can be observed that the chirality of bound states I and III are determined by the coupling strength, i.e., the chirality of bound states I and III prefers the left direction whenga>gbandvice versawhengagb.

To understand why the chirality prefers the same direction for bound states I and III no matter howδchange and why bound state II changes its chirality asδchanges,we consider the fully dimerized limits characterized byδ=±t.Most dimers yield energiesω±2t,the energy other thanω±2tare formed by the dimer connected to the two-level small atom.Discussions can be restricted to the dimers that interact with the two-level small atom, as shown in Fig.6.Whenδ=-t,four resonators are involved(see Fig.6(a)),the two-level small atom would like to emit the excitation to its left side rather than its right side.So all bound states prefer the left direction.Whenδ=t,only two resonators are involved(see Fig.6(b)).Although the two-level small atom would like to emit the excitation to thea0resonator,it can hop to theb0resonator easily.So the preferred direction of the bound states is decided by whether the ratio|β0/α0|2larger or smaller than one,

Here,εis the eigenenergy of the two-level small atom and the dimer at thej=0 cell,it can take three values,εu,εlandεm,whereεuis larger thanω+2t,εlis smaller thanω-2tandεmis within the regime(ω-2t,ω+2t).The polesE1andE2of Eq.(22)are the eigenergies in the absence ofa0resonator withE1>E2.

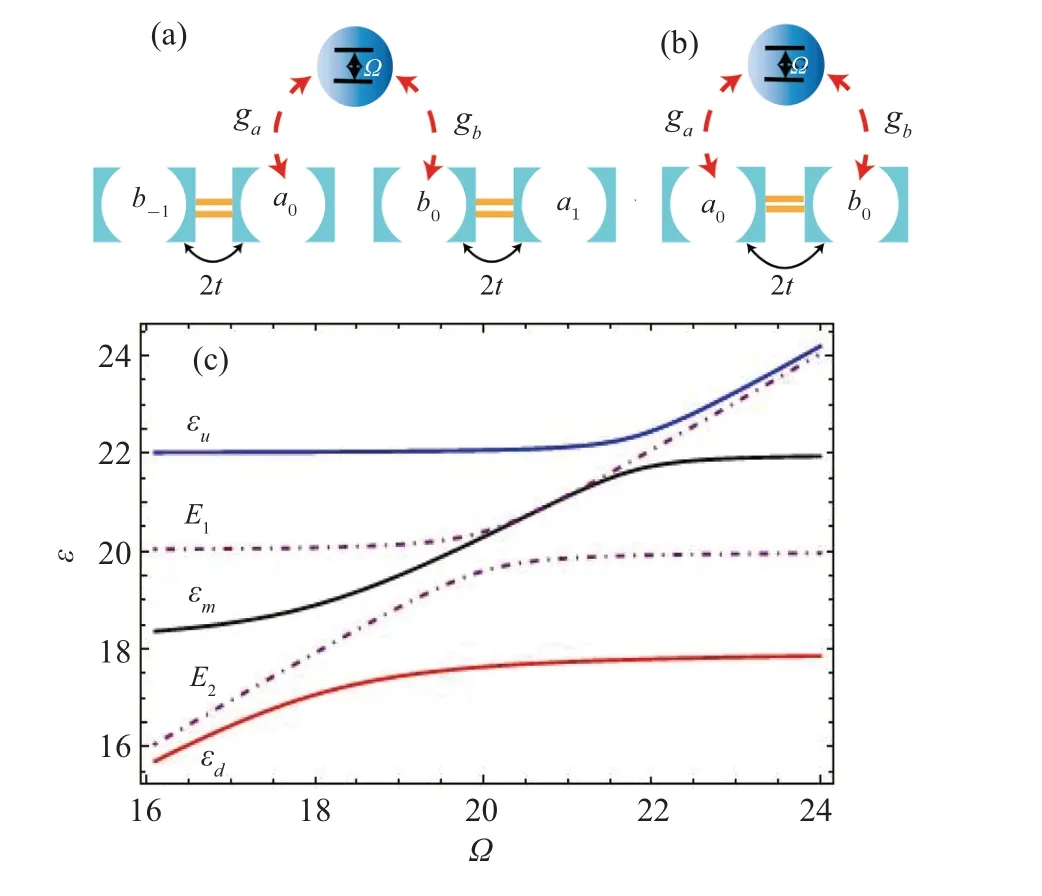
Fig.6.Sketch of the system under study when (a) δ =-t and (b) δ =t,and (c) the eigenenergy of the two-level small atom and the dimer and the poles E1 and E2 of Eq.(22)as a function of the Ω,where ω=20,ga=0.9,gb=0.4,δ =1.

In Fig.6(b), we plot the eigenergiesεandEias a function of theΩ.It can be seen thatεu>E1,εlεm>E2,which indicates that the chirality of bound state II is different from that of bound states I and III,i.e.,the chirality prefers the right direction for bound state II.The staggered coupled-resonator array is exactly described by the SSH model in Ref.[20],and the winding number of the SSH model changes from +1 forδ>0 to-1 forδ<0 discontinuously.This is the nature of the discontinunity of the chirality of the bound state II.Ifδ=0,there is no topological properties of the uniformed coupled-resonator array and thus the state II also disappear.

4.Conclusion

For an array of resonators mutually interacted with staggered hopping strengths, we consider its interaction with a two-level small atom by a coupling point or two coupling points.Its single-photon spectrum has been studied and it is found that this system has two energy bands and three discrete spectra with one lying upper the bands and one lying below the bands,and another inside the band gap.The stationary states of the discrete spectra are analytically presented and are chiral bound states when coupling strengths have different magnitudes.One can tune the chirality of bound state II over the rangeδ ∈[-t,0)∪(0,t], and continuously tune the chirality of bound states I and III over the whole rangeδ ∈[-t,t].In the case with one coupling point,the preferred direction of the chirality is controlled by the competition between the intracell hopping and the intercell hopping.In the case with two coupling points, the competition between two coupling strengths adjusts the chirality of all bound states,in addition,the chirality of bound state II change its direction asδvaries its sign for fixed coupling strengths.Due to the discontinunity of the chirality of the bound state II inheriting from the topology of the CRA,the chirality can be tuned greatly by only slightly change the magnitude ofδ.In Ref.[20],the authors proposed a tunable chiral bound states whose chirality is controllable.The coupling direction and strength between the adjacent superconductor qubits are totally controllable because they depend on the overlap of the tunable chiral bound states, which may facilitate the construction of the large scale quantum network.

Acknowledgements

Project supported by the National Natural Science Foundation of China(Grant Nos.11975095,12075082,11935006,and 12247105), the Major Sci-Tech Program of Hunan Province, China (Grant No.2023ZJ1010), and the Natural Science Foundation of Guangdong Province, China (Grant Nos.2019A1515011400 and 2023A151501223).