Holevo bound independent of weight matrices for estimating two parameters of a qubit
Chang Niu(牛畅) and Sixia Yu(郁司夏),2,†
1Department of Modern Physics&Hefei National Research Center for Physical Sciences at the Microscale and School of Physical Sciences,University of Science and Technology of China,Hefei 230026,China
2Hefei National Laboratory,University of Science and Technology of China,Hefei 230088,China
Keywords: quantum metrology, quantum Fisher information, Holevo bound, quantum multi-parameter estimation
1.Introduction
Parameter estimation is ubiquitous in our quantitative description of the physical world around us.Metrology is the science and art of how to improve the precision of our estimation.Quantum metrology,[1–5]in comparison to its classical counterpart, employs non-classical resources to improve the precision of estimations beyond the classical limits and has found numerous applications in various different fields ranging from detection of gravitational fields[10–12]to imaging of biology samples.[13]Two main non-classical resources are at our disposal, namely, the quantum mechanical states, which can encode parameters in various ways and thus give rise to different statistical models,and the quantum mechanical measurements, which can be chosen to optimize the precision of estimations.
For single-parameter estimation, the precision as quantified by the mean-square error(MSE)has a fundamental limit placed by the inverse of the quantum Fisher information(QFI),known as quantum Cram´er–Rao bound(QCRB).[14,15]QFI is in de facto a classical Fisher information (FI), which reflects the knowledge limitation of parameters in both theoretical and practical aspects,corresponding to optimal quantum measurement.Although the measurement for an optimal estimation depends on the exact value of the parameter to be estimated,there are adaptive strategies that can circumvent such a drawback.Thus for single-parameter estimation, the ultimate precision limit placed by QFI is attainable.
Simultaneously estimating multiple parameters might provide better precision than estimating them individually in the quantum scenario, which stimulated much interest in multi-parameter quantum metrology in recent years.[5–9]Unlike the case with single parameter estimation, the precision limit for classical multi-parameter estimation as placed by the classical FI matrix cannot be straightforwardly carried over to the quantum case.This is because, firstly, the optimal quantum measurements for each individual parameter might not be compatible.Secondly, the generalizations of the FI matrix to the quantum case are not unique,e.g.,two of the most well-known QFI matrices corresponding to symmetric logarithmic derivative(SLD)[14,15]and right logarithmic derivative(RLD).[16,17]A family of general logarithmic derivatives introduced by Yamagata[21]also gives rise to QFI matrices.
For multi-parameter estimation, the figure of merit in quantifying the accuracy is the MSE matrix with diagonal entries being the variances and off-diagonal entries being the covariances of the parameters.Both QFI matrices arising from SLD and RLD provide lower bounds for the MSE matrix in terms of matrix inequalities, which are also referred to as QCRBs.Generally, these bounds, which share the advantages of being explicit and intrinsic,i.e.,without reference to any weight matrix, are not always attainable.Holevo[1]proposed an asymptotically achievable bound[18–21]called Holevo bound (HB) as the ultimate limit of multi-parameter estimation.However, except for some trivial cases where the Holevo bound coincides with the QCRB arising from SLD or RLD, the Holevo bound is defined and formulated in an implicit manner, which restricts its wide applications.It is implicit in two aspects: first,it is defined by an optimization process and second, its formulation involves inevitably a weight matrix.One breakthrough is made by Suzuki[22]by deriving an analytical form of HB for a nontrivial case of estimating two parameters of a qubit.
In this work,we show that Suzuki’s analytical HB for estimating two parameters of a qubit can be further made intrinsic by removing its dependence on the weight matrices.In detail, we show that HB in this specific case is equivalent to the joint constraint imposed by two QCRBs arising from SLD and RLD.This intrinsic form in terms of pure matrix inequalities enjoys the advantage that we can determine explicitly the precise range of two variances and one covariance in the MSE matrix,which is illustrated by some examples.The rest of the paper is structured as follows.In Section 2,we briefly review the necessary background for the formulation of HB.In Section 3 we recapitulate Suzuki’s explicit HB with given weight for a 2-parameter estimation in a qubit model.Next in Section 4, we derive an explicit and intrinsic HB in this specific case.In Section 5,we analyze four different situations and illustrate the precise range of the variances and their covariance of two parameters in different statistical models.In Section 6,we prove that two QCR bounds corresponding to SLD and RLD cover all the QCR bounds corresponding to the whole one-parameter family of logarithmic derivatives introduced by Yamagata in the two-parameter qubit models.Finally,we conclude with some discussions.
2.Preliminary
To begin, let us recall some pertinent backgrounds for the formulation of Holevo bound for multi-parameter estimation.When simultaneously estimatingnparametersθ=(θ1,θ2,...,θn)encoded in a probability distribution{pµ},we employ MSE matrixCwith entries where FI matrixℱquantifies the information of parameters encoded in data.

In quantum metrology,we have at our disposal two nonclassical resources, namely, quantum mechanical states and measurements.The resulting probability distribution encodes also the information of the parameter and presents a classical estimation problem.Different choices of measurements{Mµ}which are described by a positive operator-valued measure(POVM)

However, if there are two or more parameters, QCRB can not always be simultaneously attained so the simultaneous optimization for all parameter’s precisions is unknown even though individual optimizations for every single parameter are clear.This is because the optimal measurements determined by SLDs corresponding to different parameters are in general not compatible.
The quantum version of the classical FI matrix is not unique.As an alternative,the right logarithm derivative(RLD)˜Ljis defined by
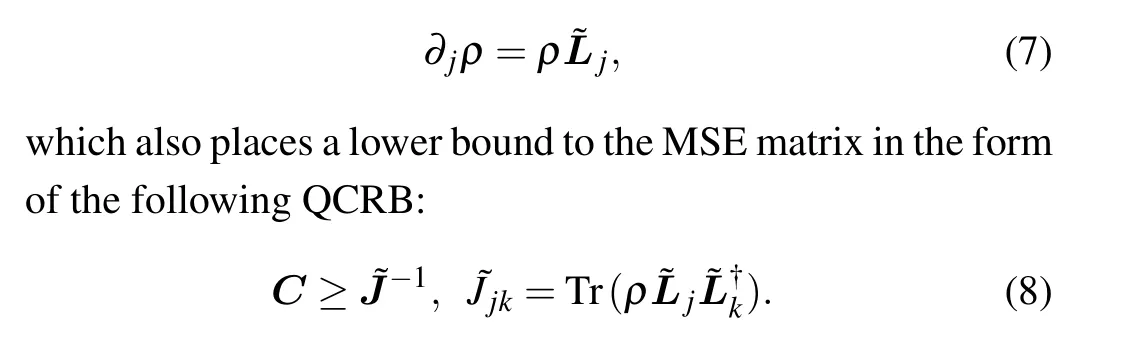
Both these two QCRBs enjoy the advantages of being explicit and intrinsic, i.e., no optimization and ad hoc weight matrix are involved, and the disadvantage of being not attainable in general.The main result of this paper is to show that these two bounds when consider simultaneously, are equivalent to the HB for estimating two parameters of a qubit,and thus can be asymptotically achieved.
By considering compatible observables Holevo proposed the so-called HB.Inevitably the formulation of HB involves a kind of weight matrixW ≥0,which is positive semidefinite.In terms of the lower bounds for the weighted trace of the MSE matrix,the HB of Nagaoka’s form reads

which holds for all measurementsMµand corresponding estimators{ˆθj,µ},from which the HB of Nagaoka’s form Eq.(9)can be derived by noting that whileCis real symmetric and ΔXis Hermitian.
3.Suzuki’s analytical Holevo bound
As mentioned above,the HBCH[W]is in general not explicitly given, i.e., optimization has to be carried out over all possible observables of form(Eq.(11))for arbitrary measurementMµand estimator ˆθj,µand depends on weight matrixW.In 2016,Suzuki[22]worked out the first instance of analytical HB for the nontrivial case of estimating two parameters in a qubit model.
Consider the scenario of simultaneously estimating two parameters,e.g.,θ1andθ2for a general mixed qubit state


Two QFI matrices are related via wheresW=Tr(W˜S).From this explicit form, we can immediately identify the QCRBC ≥J-1corresponding to SLD since the second term is always non-negative.When the second term becomes positive this bound cannot be attained.We note that the explicit HB Tr(CW)≥CH[W] withCH[W]given in Eq.(18) allows itself to be recast into a single inequality

4.Holevo bound independent of weight matrices
As shown above, the formulation of HBs, analytical or not,is implicitly formulated in terms of weight matrices.Our main result is to remove this dependence on the weight matrix to get the first instant of an explicit and intrinsic HB in a nontrivial case.
Theorem 1The Holevo bound for estimating two parameters of a qubit is equivalent to the joint constraint imposed by two QCRBs arising from SLD and RLD
ProofFirst,we shall prove that the explicit HB(Eq.(18)),which holds true for all weight matricesW ≥0 with detW=1, leads to QCRBs (Eq.(20)).As the second term in the explicit HB (Eq.(18)) is non-negative in both cases, we have TrW C ≥TrW J-1for all positive symmetric weight matrixWwith detW=1 we then get(see Lemma 1 in section 1 of the supplementary materials )C ≥J-1as bothCandJ-1are real symmetric.Furthermore,an arbitrary Hermitian 2×2 matrix ˜W ≥0 can be decomposed intoWS+iy∊withWSbeing real symmetric andy2≤detWS.Suppose|y|>0 we have detWS>0 so that we can assume detWS=1 so that|y|≤1.Then by using relation Eq.(16)we have
for an arbitrary ˜W ≥0,from which it followsC ≥˜J-1.This proves the necessity.
Second,to prove the sufficiency of constraints(Eq.(20)),we consider first the general case ˜S ̸=0, i.e.,s1·s,s2·sdo not equal to zero at the same time.Consider an arbitrary 2×2 weight matrixWsatisfying detW=1.In the 2-dimensional space in which the weight matrix lives we introduce a basis{|e〉,|˜e〉=∊|e〉}where

which is exactly the HB (Eq.(19)).Here we have denotedk=(detA)/Ae+b2and the minimum overγ>0,by derivative with respect toγ,is attained at
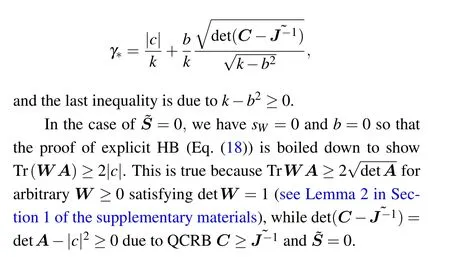
Some remarks are in order.First, according to the theorem proved above the HB is equivalent to two QCRBs arising from two kinds of QFI matrices.It should be emphasized however our main result does not imply that for a given weight matrix the Holevo bound is equivalent to the maximum of SLD bound and RLD corresponding to the same weight matrix.In fact,as shown in Section 2 of the supplementary materials,for some given weight matrixW, the solution to the following optimization:

5.Range of variances and the covariance allowed by HB
In the case of two-parameter estimation, the MSE matrixC, which is real and symmetric, has three independent variables,namely,two variancesx=C11,z=C22as diagonal entries and one covariancey=C12as the off-diagonal entry
As an immediate consequence of our theorem, the possible values ofx,y,zare determined explicitly by two matrix inequalities arising from two QCRBs.Since the relevant matrices are of dimension 2×2,those two QCRBs can be recast into the following scalar inequalities:

The choice of the weight matrix is equivalent to choosing the normal directions of some planes.
5.1.Asymptotically classical models
A model is asymptotically classical if the Holevo bound is equal to the SLD bound.In the case of the two-parameter qubit model Suzuki derived the condition under which the Holeve bound coincides with the SLD bound.[22]Here we provide an alternative proof.
Corollary 1 (Suzuki).For any two-parameter qubit model,the following three conditions are equivalent:
(i)c=0,
(ii)∀W,CH[W]=TrW J-1,
(iii)∃W>0,CH[W]=TrW J-1.
Proof 1⇒2: From Eq.(16),since ˜Sis a rank-1 projection, it follows thatJ-1≥˜J-1whenc=0 so that we have condition 2.2⇒3 is trivially true.As to 3⇒1 we note that ifCH[W0]= TrW0J-1for a given weight matrixW0> 0 then TrW0J-1is the solution to the optimization problem Eq.(24),from which it follows,according to Section 2 of the supplementary materials, the optimal MSE matrixC=J-1so thatJ-1≥˜J-1.However, from Eq.(16) it follows that det(J-1- ˜J-1)=det( ˜S+ic∊)=-c2.Thus we must havec=0.
5.2.Qubit model with two unitary parameters
We call a parameter is unitary model if the length of the Bloch vectorsis independent of the given parameter, from which it follows thatsj·s=0.If both two parameters areDinvariant we haveS=0 so thatJ-1=Re ˜J-1and the QCRBC ≥˜J-1arising from RLD is always tighter than the QCRBC ≥J-1arising from SLD.Thus there is no intersection of two determinant constraints.The range ofx,y,zis completely determined by a single matrix inequalityC ≥˜J-1.
5.3.Qubit model with one unitary parameter
Specifically we consider the following model with a Block vector given by

which is plotted in Fig.1 as the red paraboloid.We see that in this case,both QCRBs have to be taken into account.
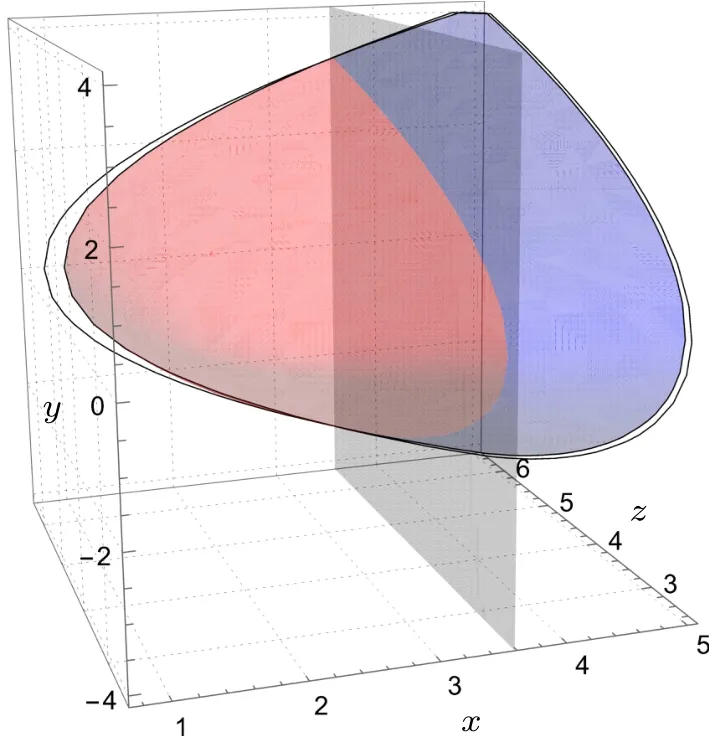
Fig.1.The explicit range of the variances x,z of t,φ, respectively, and the covariance y between t and φ in a qubit mode with only one unitary model.Here t=0.264 and k=0.640.This is the common part of the red and blue paraboloids coming from QCRBs for RLD and SLD, respectively.The surfaces of these two paraboloids intersect at a plane parallel to the y,z plane.
5.4.Qubit model without unitary parameter
Now we consider a more general model with two parameters.In this case the Bloch vector of the states=(θ1,θ2,θ3)has a lengthsthat depends on both two parametersθ1,2to be estimated, whileθ3is known and fixed.We consider also a mixed-state model with|s|<1.Obviously we haves1·s2=0 ands·sj=θj.As a result,we have the QFI matrix for SLD


Fig.2.The explicit range of the variances x,z of θ1,2,respectively,and the covariance y between θ1,2 in a more general model.Here (θ1,θ2,θ3)=(0.087,0.315,0.540).The range is the common part of the red paraboloid coming from QCRB for RLD and the blue one coming from QCRB for SLD.The surfaces of these two paraboloids intersect at a general plane.
6.Weightless form of the maximum logarithmic derivative bound
Quite recently,[25]Yamagata introduced a particular oneparameter family of generalized logarithmic derivatives,each of which gives rise to a QCRB.Specifically, for each real 0≤β ≤1 a generalized logarithmic derivativeLβj, referred to asβ-LD,can be defined by



(v)Joint QCRBs from allβ-LD
The equivalence between bounds 1 and 2 is due to Suzuki,between bounds 2 and 4 is established in our theorem,and between bounds 4 and 5 has been established in the discussions above.The equivalence between bounds 2 and 3,due to Yamagata,can be directly established by substituting Eq.(32)into Yamagata’s bound,which turns out to be a quadratic function of|β|
After taking the maximum over|β|≤1 we can obtain Suzuki’s explicit bound Eq.(18).We note that the first three bounds involve the weight matrices while the last two bounds are expressed intrinsically,i.e.,without referring to any weight matrices.We note that bound 5 is a general bound for all possible estimation models.
7.Summary
We have derived the first instance of intrinsic Holevo bound without involving any weight matrice in a nontrivial case,namely,for estimating two parameters of a qubit,based on Suzuki’s analytical Holevo bound.It turns out that HB is equivalent to the joint constraint imposed by two QCRBs coming from RLD and SLD.The relation to Yamagata’s maximum logarithmic bound is clarified.With the help of this explicit form of HB in terms of pure matrix inequalities,we are able to explicitly determine the range of two variances and a covariance in the MSE matrix characterizing the precision,allowed by HB.As examples,we plot these ranges in the cases of qubit models with different numbers of unitary parameters.Finally,we point out the particularity of SLD and RLD QFI matrices among all monotone QFI matrices in this kind of models.Due to the pivotal role played by the HB in quantum multiparameter estimations, our result sheds new insight into the relations between Holevo bound and quantum Cram´er–Rao bounds.We conjecture that there are similar weightless forms for Holevo bounds,(e.g.,bound 5 in Corollary 2)in more general cases.
Acknowledgment
Project supported by the Key-Area Research and Development Program of Guangdong Province of China (Grant Nos.2020B0303010001 and SIQSE202104).
- Chinese Physics B的其它文章
- Unconventional photon blockade in the two-photon Jaynes–Cummings model with two-frequency cavity drivings and atom driving
- Effective dynamics for a spin-1/2 particle constrained to a curved layer with inhomogeneous thickness
- Genuine entanglement under squeezed generalized amplitude damping channels with memory
- Quantum algorithm for minimum dominating set problem with circuit design
- Protected simultaneous quantum remote state preparation scheme by weak and reversal measurements in noisy environments
- Gray code based gradient-free optimization algorithm for parameterized quantum circuit

