Multiple mixed state variable incremental integration for reconstructing extreme multistability in a novel memristive hyperchaotic jerk system with multiple cubic nonlinearity

Meng-Jiao Wang(王梦蛟) and Lingfang Gu(辜玲芳)

School of Automation and Electronic Information,Xiangtan University,Xiangtan 411105,China

Keywords: extreme multistability,hyperchaotic,jerk system,nonlinearity

1.Introduction

In recent years, chaotic systems have gradually become a popular issue in nonlinear scientific research due to their complex phenomena in nonlinear systems.[1–10]In general, a system with one positive Lyapunov exponent(LE)is called a chaotic system and a chaotic system with at least two Lyapunov exponents (LEs) greater than zero is called a hyperchaotic system.[11–13]Hyperchaos belongs to a kind of chaos but since hyperchaotic systems have at least two positive LEs,their dynamical behavior folds and expands in more directions,and the dynamic properties of hyperchaotic systems are more complex than those of chaotic systems.Therefore,they have a wider prospect for application.[14,15]

The phenomenon of initially correlated multistability is a unique phenomenon for nonlinear dynamical systems and is essential in the search for potential uses in chaotic engineering applications.[16–18]Multistability is the property of multiple different types of attractors coexisting under the same set of system parameters.[19–23]In other words,when the system parameters are fixed, different initial conditions will induce the system to enter different orbits, resulting in very different attractors.[24,25]When the number of coexisting attractors in the same set of parameters tends to infinity, then the system has extreme multistability.[26]Multistability is an intrinsic property of many nonlinear systems and it allows the system to switch between different states without adjusting the parameters, thus increasing the flexibility of the system.Consequently, multistability has become an important research topic.[22,23]Moreover, due to the complexity of hyperchaotic systems, the discovery of extreme multistable hyperchaotic systems is relatively rare.

Due to the special intrinsic structure relationship of ideal memristors,chaotic systems based on memristors usually exhibit extreme multistability phenomena.They generally have no equilibrium points or have line equilibrium points[27–29]or surface equilibrium points[30,31]related to the initial conditions;therefore,they are difficult to operate stably in the long term.Since memristors are often described as dynamic components in the flux-charge domain,the flux and charge can be used as state variables of the system and modeled in a reducedorder form for memristor circuits, which can effectively simplify the system analysis.With this transformation,the initial values of the primitive system can be represented as parameters of the reduced-order system, and the initial relevant dynamical behavior of the primitive system can be shown in the flux-charge domain.Therefore, the incremental flux-charge analysis method[33,34]can easily be used in the study of relatively complex memristive circuits.

Based on the duality of circuit variables,[35]memristive chaotic circuits made up of linear discrete electronic components can easily be modeled as flux-charge.Since flux and charge are time integrals of voltage and current,the basic principle of flux analysis methods is the incremental integral transformation of state variables,[31]so memristive systems with normalized state variables can be modeled using the incremental integral transformation for order reduction.However,since the integration of higher-order nonlinear terms is difficult to express explicitly, this method can only deal with memristor systems without complex nonlinear terms other than memristors.[28]

To address both of these issues, a hybrid state variable incremental integration (HSVII) method consisting of incremental integral transformations of state variables and linear transformations has been proposed in Ref.[28].In this paper, a multiple mixed state variable incremental integration(MMSVII) method is proposed based on the HSVII method to solve amnesiac hyperchaotic jerk systems with multiple distinct cubic nonlinear terms.The validity of the proposed method is demonstrated with a four-dimensional memristive hyperchaotic jerk system with two distinct cubic nonlinearities.This four-dimensional amnestic hyperchaotic jerk system has three line equilibria and a large number of coexisting attractors.As a result, it is not easy to measure stably in a hardware circuit.Using the proposed method,the incremental integral transformation is carried out first,and then the integral of the cubic nonlinear term is represented by the newly introduced state variable.However,the new mapping suffers from a certain degree of divergence in the different state variables.In addition, in combination with the characteristics of the equation,the difference between the 1st and 5th state variables and the sum of the 3rd and 4th state variables are selected as the two new state variables, respectively.Through this method,the divergence problem has been successfully solved and a three-dimensional reduced-dimension system has been constructed, which facilitates the mechanistic analysis and physical measurements of the initial state-dependent dynamics of the primitive system.Numerical simulations and simulation experiments demonstrate that the coexisting attractors of the initial four-dimensional memristive hyperchaotic jerk system varying with the initial state of the memristive can be visualized in the reduced-dimension system.

In this paper,a four-dimensional memristive hyperchaotic jerk system is proposed in Section 2, whose extreme multistability phenomena are revealed numerically by bifurcation diagrams, LEs spectra, and phase diagrams.In Section 3, a dimensionality reduction model of this dimensional memristive jerk hyperchaotic memristive system is constructed based on the HSVII.The mechanism for the generation of the initial correlation dynamics is explored by analyzing the stability of the equilibrium point.Finally,in Section 4,simulation circuit experiments are carried out to verify the theoretical and numerical results.

2.A memristive hyperchaotic jerk system with three linear equilibrium points

2.1.Mathematical models

The American scientist Sprott proposed the jerk system in 2000,[36]which is mathematically modeled as

whereβ=0.45–0.7, whenf(x1)=|x1|-1, a single scroll chaotic attractor is produced; whenf(x1)=sgn(x1)-x1, a double-scroll chaotic attractor is produced.

The flux-controlled memristor[37]used in this paper is

whereq(ϕ) is a nonlinear function andϕis magnetic flux.The incremental memductance function is

To verify the characteristics of the memristor, a bipolar sinusoidal voltage is applied across the memristor.When the frequencyFmis 0.5, 2 and 8 for a fixed amplitudeAm=2,three “8” shaped hysteresis lines are generated, as shown in Fig.1(a), and it is found that the flap area of the “8” shaped hysteresis lines shrinks asFmincreases.When the frequency is fixed atFm=2 and the amplitudeAmis 1,2 and 3,three“8”shaped hysteresis lines are generated as shown in Fig.1(b),and the flap area of the “8” shaped hysteresis lines can be found to expand asAmincreases.In summary, it can be seen that the model satisfies the fingerprint characteristics associated with the memristor.

Fig.1.The relationship between voltage and current for the memristor.(a)Am=2,(b)Fm=2.

By introducing this memristor into the first equation of the original jerk system and adding the fourth equation as the internal equation of state of the memristor, as well as adding some linear and nonlinear terms to the second and third equations,a new four-dimensional jerk memristive chaotic system can be constructed with the following mathematical model:

where parametersaandbare set to 0.68 and 20, respectively, and when the initial conditions of the model are set tox2(0)=10-6andx1(0)=x3(0)=x4(0)=0, the memristive jerk system generates a double-scroll chaotic attractor,as shown in Fig.2.

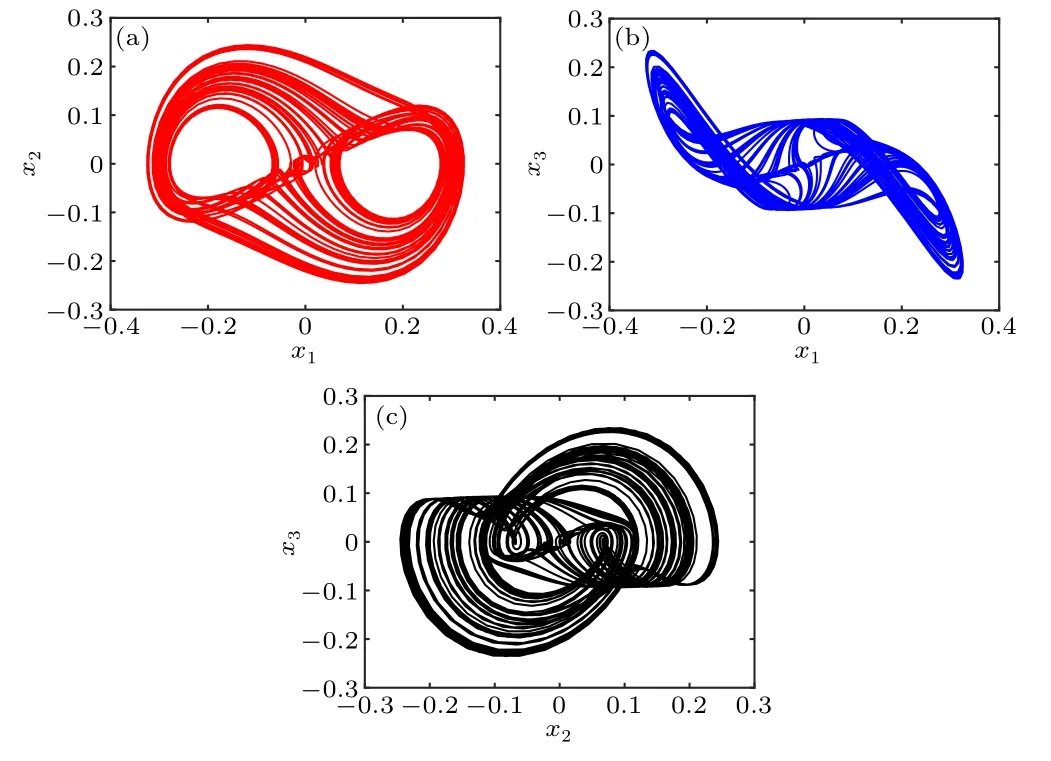
Fig.2.Phase diagram of the double-scroll chaotic attractor generated by the memristive jerk system when a=0.68, b=20, x1(0)=x3(0)=x4(0)=0.(a)Phase portrait in the x1–x2 plane.(b)Phase portrait in the x1–x3 plane.(c)Phase portrait in the x2–x3 plane.

2.2.System dynamics analysis

2.2.1.LEs spectrum and bifurcation diagram

When the initial conditionx4(0) of the memristor changes, the dynamical behavior of the system will also change greatly.Takingx4(0) as the change parameter, the bifurcation diagram and the corresponding LEs spectrum are shown in Fig.3.It is clear that the stable and unstable state regions reflected by each trajectory in the diagram are consistent.The system exhibits complex dynamical behaviors, including periodic attractors, chaotic attractors, proposed periodic attractors,tangential bifurcations,doubly periodic bifurcations,inverse doubly periodic bifurcations, and crises.Observation of the LEs spectrum reveals that in the interval(-0.2,0.5),asx4(0) gradually increases, LE1 is always positive, while LE2 is sometimes positive and sometimes negative, thus alternating between hyperchaotic and chaotic states of motion of the system.

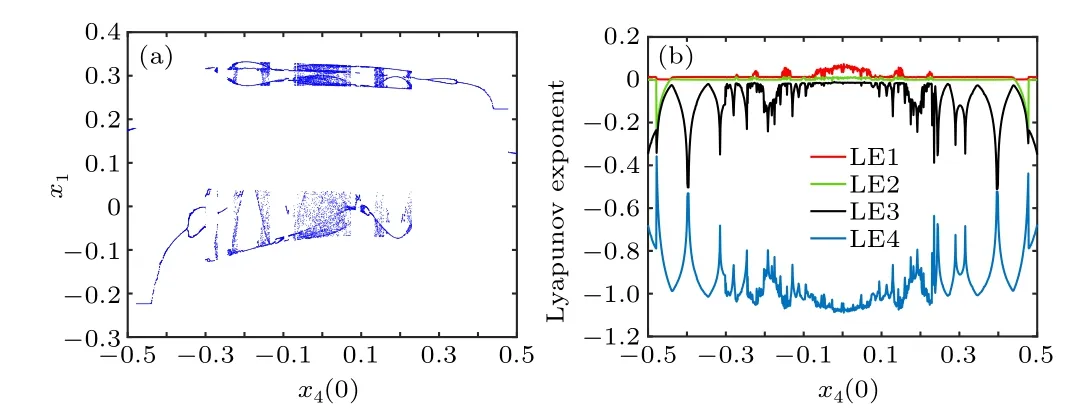
Fig.3.Bifurcation diagram and LEs spectrum of the memristive jerk system with respect to when a=0.68,b=20,x2(0)=10-6,x1(0)=x3(0)=0.(a)Bifurcation diagram,(b)finite time LEs spectra.

Furthermore, the coexistence bifurcation behavior with respect to parameterawhen the initial conditions of the system(1)are set to(0,10-6,0,0)and(0,-10-6,0,0),respectively, is shown in Fig.4.It is not difficult to observe that within the interval (0.6,1.2), with the increase of the value of parametera, the system enters period 1 after experiencing chaos,periodic window,and bifurcation,respectively,and then enters short chaotic mode through twice period-doubling bifurcation, and finally reaches the stable point through antiperiod-doubling bifurcation and twice period-doubling bifurcation.

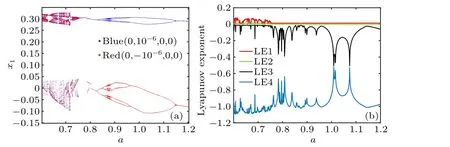
Fig.4.Bifurcation diagram and LEs spectrum of the memristive jerk system with respect to the parameters when a=0.68, b=20, x2(0)=10-6,and x1(0)=x3(0)=0.(a)Bifurcation diagram,(b)finite time LEs spectra.

2.2.2.Extreme multistability of system

From the bifurcation diagram and the LEs spectrum, it can be seen that the initial conditions have a strong influence on the dynamical behavior of the system and that the system (1) produces various attractors under different initial conditions of the memristor,which means that there is extreme multistability in the system.Some of the typical attractors are shown in Fig.5.We can also find that tiny changes in the initial conditions of the memristor can lead to significant changes in the phase diagram of the system,which also reflects the high sensitivity of chaotic systems to initial conditions.

Fig.5.Memristive chaotic system with various attractors generated under different initial condition.(a) x4(0)=-0.7, (b) x4(0)=-0.31, (c)x4(0)=-0.27,(d)x4(0)=-0.23,(e)x4(0)=-0.16,(f)x4(0)=-0.14.

2.2.3.Equilibrium points and stabilities

Zero the right-hand side of system(1),i.e.,

Forb ≥0,it is clear that the equilibrium points of the system can be given by the following equation:

whereγis an arbitrary constant,so that system(4)has threeline equilibrium points parallel to thex4-axis.For the Jacobi matrix at the equilibrium points can be expressed as

It can be found that the position of the trilinear equilibrium point is determined by the system parameterband the initial conditionx4(0)of the memristor,while its stability is determined by the system parameteraand the initial conditionx4(0)of the memristor.

Fig.6.For S0,the distribution of eigenvalues about γ.(a)Real,imaginary parts of the eigenvalues on γ,(b)real parts of the eigenvalues on γ.

The eigenvalue curves forS0are shown in Fig.6, whereλ1andλ2are real eigenvalues,λ3andλ4are a pair of complex conjugate eigenvalues,and it can be seen from the Fig.6 that forγ<-1.073 andγ>1.073,S0is a saddle focus for indicator 2; for-1.073<γ<1.073,S0is a saddle focus for indicator 1.The eigenvalue curves forS+andS-are shown in Fig.7.Similarly,forγ<-0.961 andγ>0.961,S±is the saddle focus of both indicators 1;for-0.961<γandγ>0.961,S±is the saddle focus of both indicators 2.

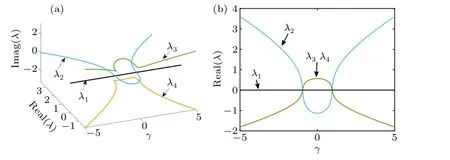
Fig.7.For S+ and S-,the distribution of eigenvalues about S0.(a)Real,imaginary parts of the eigenvalues on γ,(b)real parts of the eigenvalues on γ.

3.Dimensionality reduction modeling through the MMSVII method

System(4)can easily be implemented using resistors,capacitors,multipliers,and operational amplifiers,but it is difficult to set up the initial conditions of the system in a hardware circuit with strict accuracy.To address this issue,we adopt the MSVII method to reduce the dimensionality of the proposed four-dimensional memristive hyperchaotic jerk system.This results in a three-dimensional reduced model that maps the initial state of the original system to its parameters.The reduced model can effectively analyze the dynamical behavior mechanism and control related to the initial values of the original system, making it easier to capture the extreme multistability phenomenon related to initial values in hardware circuits.

3.1.Incremental integral transformations of state variables

The difference of squares formula is then used and simplified to give

Deriving Eq.(19)and substituting it into Eq.(18)gives

As the special intrinsic structure relation of the memristor,the higher-order integral terms associated with the memristor can be represented by the state variables of the new mapping, whereas for the higher-order terms of the second and third equations, it is difficult to represent them.To solve this problem,new state variables can be defined as

From Eq.(10), the initial value of system (18) is 0.However, whenσ2=10-6,σ1=σ3=σ4=0, the trajectory of system(18)gradually begins to expand,as shown in Fig.8.

3.2.Linear transformation of state variables

Looking at Fig.8,one can see that the system diverges to some extent in all planes,and a synthesis of Ref.[13],together with the characteristics of the three equations of the system,allows for the introduction of three new state variables as

Since the initial valuesX1(0),X2(0),X3(0), andW(0) of the system (18) are both 0, the initial valuesY1(0),Y2(0), andY3(0) of the system (20) are also fixed to 0.When the parameters of system(20)are set to be the same as those of system(18),the phase diagram of the system is shown in Fig.9.It is clear that the method of dimensionality reduction modeling of the system proposed in this paper can effectively eliminate divergence.

Fig.8.Phase diagram of system(18)when a=0.68,b=20,σ2=10-6,and σ1=σ3=σ4=0.(a)X1–X2 plane,(b)X1–W plane,(c)X2–W plane,(d)X2–V plane.

Fig.9.Phase diagram of system(20)when a=0.68,b=20,σ2=10-6,and σ1=σ3=σ4=0.(a)Y1–Y2 plane,(b)Y1–Y3 plane,(c)Y2–Y3 plane.

Comparing system (20)with system(4), it can be found that the final system obtained is related to the initial system(4)as

LetZ1=x1(t),Z2=x2(t),Z3=x3(t), andZ4=x4(t).The phase diagrams drawn from the relations described in Eq.(21)are shown in Fig.10;it can be noticed that they show the same topology as the initial system(4).

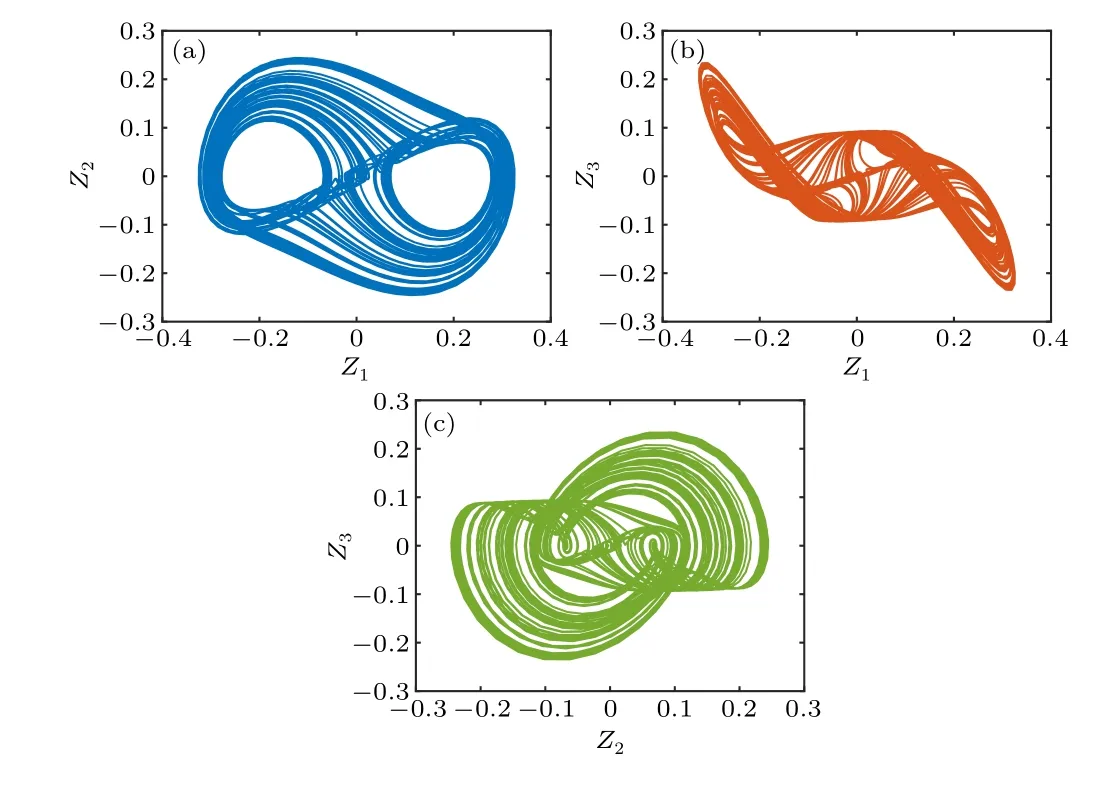
Fig.10.Phase diagram of system(21)when a=0.68,b=20,σ2=10-6,and σ1=σ3=σ4=0.(a)Z1–Z2 plane,(b)Z1–Z3 plane,(c)Z2–Z3 plane.

3.3.Switching equilibrium points and stabilities

Let ˙Y1= ˙Y2= ˙Y3=0,

When the parameterσ4is a variable anda=0.68,b=20,σ1=0,σ2=10-6,σ3=0, this gives the Jacobian matrix of the system at the equilibrium point

Fig.11.The equilibrium point is about the position and stability of the parameter σ4,(a)E1,(b)E2,(c)E3,(d)E4,(e)E5.

Table 1.The type of the equilibrium points of parameter σ4.

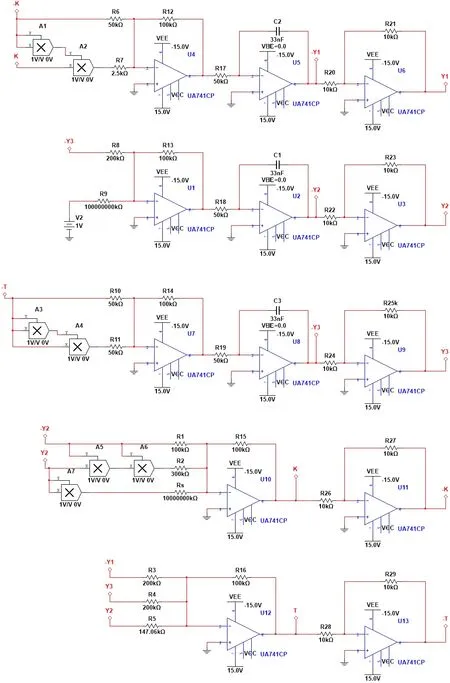
Fig.12.Multisim simulation circuit diagram for system(20).

4.Multisim digital circuit implementation

To verify the results of the MATLAB numerical simulation, a Multisim equivalent circuit for system (20) was constructed, based on Eq.(20) and the basic operational circuit modules(summation, integration, inverse, etc.), using an equivalent circuit model designed with components such as resistors, capacitors, operational amplifiers, and analog multipliers.Through Kirchhoff’s laws, we can obtain the circuit equations of the system(20)can be expressed as The circuit diagram and simulation results for system(20)are shown in Figs.12 and 13.In addition, the phase diagram of the system (20) was also numerically simulated for different values ofσ4,as shown in Figs.14(a)–14(f).

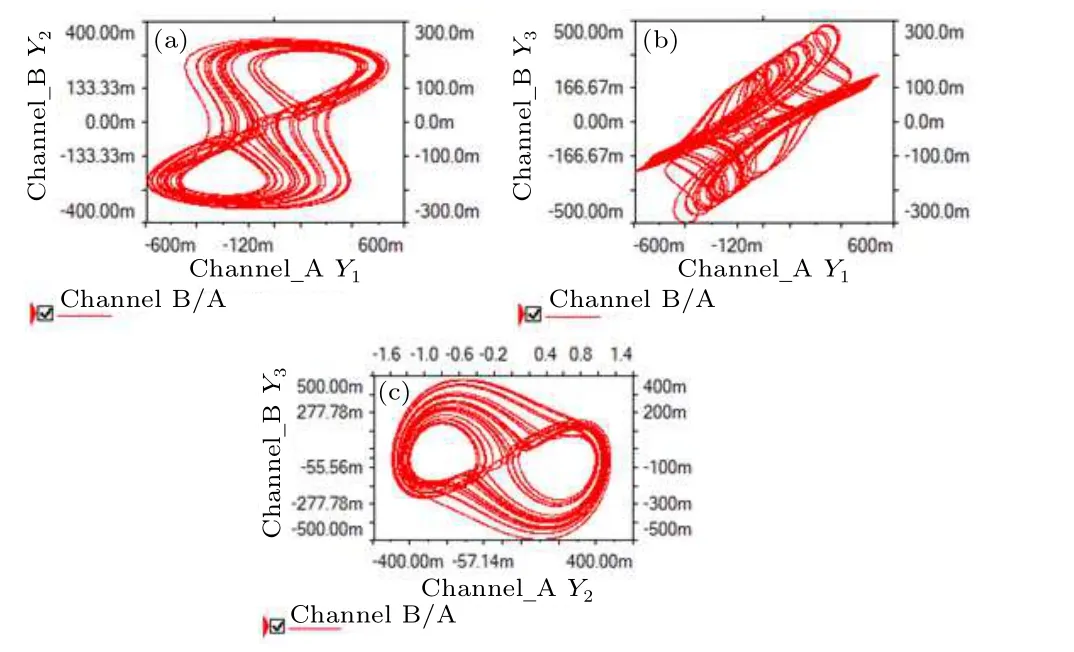
Fig.13.Multisim simulation results for system (20).(a) Y1–Y2 plane,(b)Y1–Y3 plane,(c)Y2–Y3 plane.

Fig.14.Simulation results for various attractors generated by the system(20)with different values of σ4: (a)x4(0)=-0.7,(b)x4(0)=-0.31,(c)x4(0)=-0.27,(d)x4(0)=-0.23,(e)x4(0)=-0.16,(f)x4(0)=-0.14.

5.Conclusion

In this paper,a four-dimensional memristive hyperchaotic jerk system is obtained by adding an ideal memristor to the jerk chaotic system.This four-dimensional memristive hyperchaotic jerk system has three equilibrium points controlled by the system parametersband the initial conditionx4(0).Thus,with the system parametersaandbheld constant,the system generates multiple coexisting attractors as the initial value of the memristor changes, resulting in an extreme multistability phenomenon.

To explain the control mechanism of extreme multistability phenomena from within, this paper uses a method consisting of incremental integral transformations of state variables and linear transformations to reconstruct and model this memristive jerk system,successfully constructing a threedimensional reduced-dimension system that maintains the dynamics of the original four-dimensional system.A phase diagram based on the relationship between the primitive system and the reduced-dimension system then reveals that the method can be very effective in solving the divergence problem arising from the newly mapped state variables.Finally,based on this reduced-dimension model, extreme multistability phenomena with a large number of coexisting attractors are explained by analyzing the deterministic equilibrium points of the system.In addition, Multisim simulated circuit simulations of the reduced-dimension system are carried out,and the simulation results are in agreement with the MATLAB numerical simulation results.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant No.62071411)and the Research Foundation of Education Department of Hunan Province, China(Grant No.20B567).