一类独立数为4图的结构研究

周秀君

(广东纺织职业技术学院基础部，广东 佛山 528041)

一类独立数为4图的结构研究

周秀君

(广东纺织职业技术学院基础部，广东 佛山 528041)

图论研究中一个很重要的方面是利用图的各种参数来刻画图的结构。通过对图的2个重要参数-独立数和连通度的研究,给出独立数4,而连通度不超过1图的结构特征。

独立数；连通度；完全图；哈密顿图

1 基本概念

仅考虑简单图,下面出现但未介绍的定义和图论术语参看文献[1,2]，G=(V(G),E(G)),V(G)表示G的顶点集，E(G)表示G的边集。对∀u∈V(G),NG(u)={v|uv∈E(G),v∈V(G)}。若H⊆G，则NH(u)={v|uv∈E(H),v∈V(H)}。α(G)和κ(G)分别表示G的独立数和连通度。用A=B定义A就是B。如果图G含一个生成圈，则称G是哈密顿的。哈密顿路是图生成图，简称为哈路。(x,y)-哈路是图中以x和y为2端点的生成路。若G=(V(G),E(G))，对∀u,v∈V(G)，都有uv∈E(G),则称G是完全图。若H1和H2是图G的2个导出子图，则H1-H2和H1∪H2分别表示G中由V(H1)-V(H2)和V(H1)∪V(H2)的导出子图。H1⨁H2定义为H1∪H2且V(H1)∩V(H2)=Φ。文献[2-4]给出了图的独立数为1，2或3，而连通度任意取值时图的结构特征。下面，笔者研究独立数为4，而连通度不超过1图的结构特征。

首先定义10类图：

K={G:G是完全的}HH={G：G是哈密尔顿的}

G0={G=H1⨁H2,Hi∈K,i=1,2,α(G)=2}

G1={G=H1⨁H2⨁H3,Hi∈K,i=1,2,3,α(G)=3}

G2={G=H1⨁H2,H1∈K,H2∈HH,α(G)=3}

G4={G=H1⨁H2,H1∈K,H2∈G2,α(G)=4}

G5={G=H1⨁{x}⨁H2,H1∈K,H2∈HH,α(G)=4}

G6={G=H1⨁H2,α(H1)=α(H2)=2,α(G)=4}

G7={G=H1⨁H2,H1∈K,H2∈HH,α(G)=4}

2 相关引理

引理1[3]令G是一个阶为n(n≥3)的图，如果α(G)≤κ(G)，那么G是哈密顿的。

引理2{x1,x2}是G的一最小割点集，H是G-(x1,x2}一个连通分支，其中α(H)=κ(H)=2。令H′=G[V(H)∪{x1,x2}]，则下列结论至少有一个成立:

(1)H′中有(x1,x2)-哈路;

证明令{y1,y2}是H的一割点集，H-{y1,y2}有2个连通分支Hi,Hi∈K,i=1,2。不妨设min{|H1|,|H2|}≥2。由于α(H)=2，因此(N(y1)∪N(y2))∩V(Hj)⊇V(Hj),j=1,2。于是，G[V(Hi)∪{y1,y2}]有(y1,y2)哈路Pi,i=1,2。

先设G[V(Hi)∪{x1,x2}]有(x1,x2)-哈路，i∈{i,2}。易知H′中有(x1,x2)哈路，即(1)成立。

下考虑G[V(Hi)∪{x1,x2}]没有(x1,x2)-哈路的情形，i=1,2。

引理3{x1,x2}是G的一最小割点集，H是G-{x1,x}一个连通分支，其中H∈G0,设H=H1⨁H2,H1含H的一割点x。则下面2个结论至少一个成立：

(1)G[V(H)∪{x1,x2}]有(x1,x2)-哈路；

(2)α(G[V(H)∪{xi}])=3,i∈{1,2},且G[V(H2)∪{x1,x2,x}]或G[V(H2)∪{x1,x2}]有(x1,x2)-哈路。

证明不妨设G[V(H2)∪{x,x2}]有(x,x2)-哈路P。若N(x1)∩V(H1)/{x}=，则G[V(H1)∪{x1}]有(x1,x)-哈路。它和P形成G[V(H)∪{x1,x2}]中(x1,x2)-哈路，此时(1)成立。

下设N(x1)∩V(H1)/{x}=Φ,则N(x2)∩V(H1)/{x}=Φ。于是，G[V(H1)∪{x2}]有(x,x2)-哈路Q。如果G[V(H2)∪{x,x1}]有(x,x1)-哈路，则它和Q形成G[V(H)∪{x1,x2}]中(x1,x2)-哈路，此时(1)成立。否则，N(x1)∩V(H2)=Φ或|(N(x1)∪N(x))∩V(G2)|=1。若N(x1)∩V(H2)=Φ，则N(x1)∩V(H1)={x}，故x1x和P形成G[V(H2)∪{x1,x2,x}]中(x1,x2)-哈路。若|(N(x1)∪N(x))∩V(H2)|=1，则G[V(H2)∪{x1,x2}]有(x1,x2)-哈路。选取u1∈V(H1)/{x},u2∈V(H2)/N(x1),使得{u1,u2,x1}是独立集。因此α(G[V(H)∪{x1}]=3。此时(2)成立。故引理3成立。

3 主要结论的证明

定理1如果α(G)=2，则G∈HH∪G0。

证明若κ(G)≥2，根据引理1，则G∈H。下设κ(G)≤1。

先设κ(G)=1。令x是G的一割点，则G-x有2个连通分支H1和H2，这里H1和H2都是完全图。由于α(G)=2，则Hi⨁{x}至少有一个完全图，i=1,2。因此G=G|V(Hi)∪{x}]⨁H3-i∈G0。

再设κ(G)=0，则G有2个连通分支H1和H2，这里H1和H2都是完全图。由于α(G)=2，则Hi至少有一个是完全图，i=1,2。因此G=V(Hi)⨁H3-i∈G0。故定理1成立。

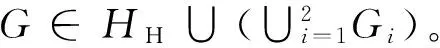
证明若κ(G)≥3,根据引理1,则G∈H。下设κ(G)≤2,分成3种情形讨论。

情形1κ(G)=0。令G有t个连通分支H1,…,Ht,可知2≤t≤α(G)=3。若t=3，由于α(G)=3,则H1,H2,H3都是完全图，则G∈G1。下设t=2。不妨设α(H1)≤α(H2)。由于α(G)=3,则α(H1)=1和α(H2)=2。根据定理1，H2∈H∪G0，故G∈G1∪G2。

情形2κ(G)=1。设x是G的一割点，G-x有t个连通分支H1,…,Ht,可知2≤t≤α(G)=3。若t=3，由于α(G)=3，因此α(Hi)=1,i=1,…,3,且∃j∈{1,2,3}，使得Hj∪{x}∈K。故G∈G1。

证明令G有t个连通分支H1,…,Ht。可知2≤t≤α(G)=4。若t=4，由于α(G)=3,则H1,…,H4都是完全图，则G∈G3。

下设t=3。不妨设α(H1)≤α(H2)≤α(H3)。可知α(H3)≤α(G)-α(H1)-α(H2)≤2。由于α(G)=4，则α(H1)=α(H2)=1和α(H3)=2。根据定理1，H3∈HH∪G0，故G∈G3∪G4。

证明设x是G的一割点，G-x有t个连通分支H1,…,Ht,可知2≤t≤α(G)=4。先设t=4,由于α(G)=4，因此α(Hi)=1,i=1,…,4，且存在j∈{1,2,3,4}，使得Hj∪{x}∈K,故G∈G3。

其次设t=3。不妨设α(H1)≤α(H2)≤α(H3),于是：

α(H3)≤α(G)-α(H1)-α(H2)≤4-1-1=2

先设α(H1)=1和α(H2)=2，由定理1知，H2∈HH∪G0。若H2∈HH,则G=H1⨁{x}⨁H2∈G5。若H2∈G0，则H2=H21⨁H22,H21和H22都是完全的。于是，G=H1⨁{x}⨁H21⨁H22∈G3。

[1]Bondy J A,Murty U S R.Graph Theory with Applications[M].New York:The Macmillan Press LTD,1976.

[2]Enomoto H.Long Cycles in Triangle-free Graphs with Prescribed Independece Number adn Connectivity[J].J Combinatorial Theory,Series B,2004,91:43-55.

[3]Chvátal V，Erdös P.Anote on Hamiltonian circuits[J].Discrete Math,1972,2:111-113.

[4]吴亚平，冯丽珠.独立数小于4图的结构研究[J].长江大学学报(自然科学学报)：理工，2007,4(4):29-32.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.03.001

O157.5

1673-1409(2011)03-0001-03