一种五自由度机械臂逆运动学求解的几何法
朱晓龙,顿向明
(上海交通大学机械与动力工程学院,上海200240)
0 引言
目前,常用的机械臂逆运动学求解方法主要可以分为3种:代数法、迭代法[1-4]和几何法[5-8],其中代数法最为通用。代数法的求解思想是将运动学正向求解方程的两侧依次乘以各个变换矩阵的逆矩阵,从而分离出易于求解的关节角变量,进而进行求解。但对于五自由度机械臂,由于其自由度数不足6,不能以任意姿态逼近同一目标位置,进而造成在笛卡尔空间轨迹规划所得到的轨迹节点目标位姿不存在运动学逆解,且逆解存在与否难以直观判断。因此,传统的在笛卡尔空间进行轨迹规划,并利用代数逆解法求取目标位姿对应的关节角度值的方法对于五自由度机械臂的运动算法设计不太适合。
1 机械臂模型及正运动学求解
以多关节单电机离散驱动的五自由度机械臂为研究对象,其结构简图如图1所示。机械臂5个关节全部为旋转关节,其中,3个为弯曲关节,2个为扭转关节。机械臂驱动方式与机械结构较为特殊,但其运动学模型较为通用,具有一定的代表性。
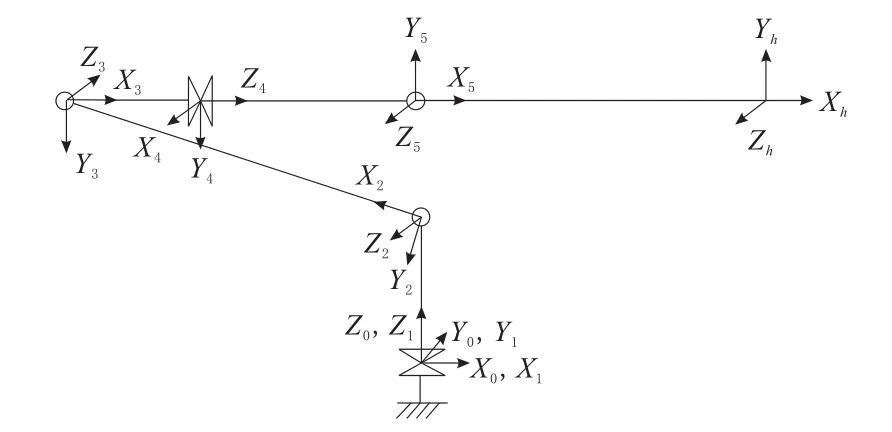
图1 机械臂结构
机械臂正运动学求解相对于逆运动学求解较为简单,只需根据运动学模型,通过对各连杆坐标系变换矩阵进行运算就可以求得末端坐标系在基础坐标系下的惟一位姿矩阵。为了方便后续几何法运动学逆解的计算,这里各连杆坐标系的建立未完全按照D-H法[9]进行,具体坐标系建立情况如图1所示。X0Y0Z0为基础坐标系,X1Y1Z1,X2Y2Z2,X3Y3Z3,X4Y4Z4,X5Y5Z5分别为5个连杆坐标系,XhYhZh为方便末端轨迹规划而建立的末端坐标系。图1中,从基础坐标系附近开始,5个连杆的长度分别为89.0mm,245.9mm,85.0mm,147.0mm,231.7 mm。图1对应的机械臂姿态为其机构零位,各关节角度变量的取值范围以及零位状态下对应的关节角度初始值如表1所示。
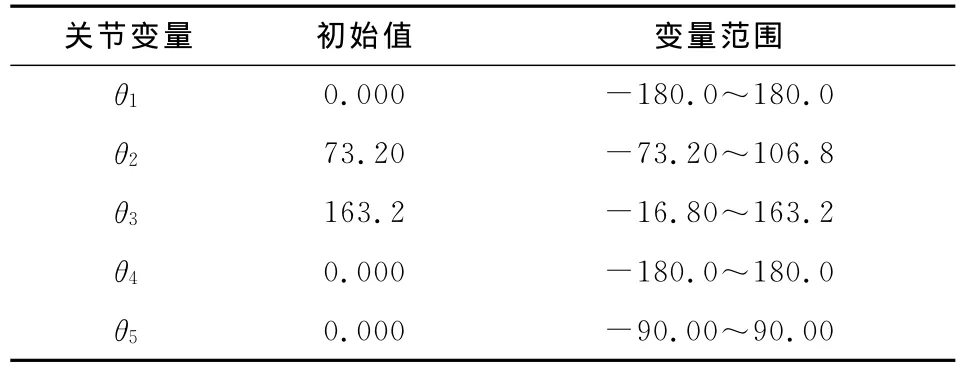
表1 关节转角变化范围及当前值 (°)
根据机械臂的运动学模型以及相邻连杆坐标系间的位姿关系,可以建立相邻连杆坐标系间的变换矩阵如下:

Ci(i=1,2,…,5)代表cosθi,Si(i=1,2,…,5)代表sinθi。将各个坐标系位姿变换矩阵顺序相乘,即可得到末端连杆坐标系的位姿矩阵:
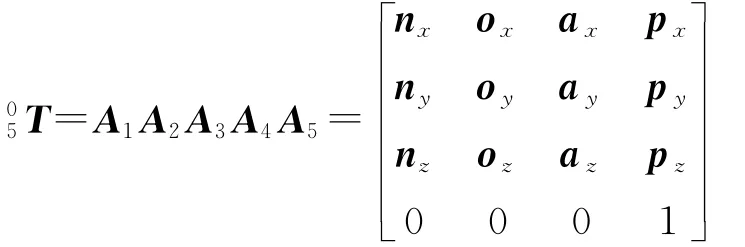
n,o,a3个向量描述了机械臂末端连杆的姿态,向量描述了末端连杆的位置,这4个向量的各个元素是5个关节角变量的函数。
2 几何法运动学逆解
2.1 末端坐标系位姿描述方法
对于五自由度机械臂而言,由于自由度小于6,其可达空间内的目标位置点不能以任意姿态逼近。因此,传统的采用3个笛卡尔位置坐标和3个欧拉角坐标描述机械臂末端坐标系位姿的方法约束了过多的自由度,在末端轨迹规划时如用这种描述方式进行变量插补,所得到的目标位姿矩阵无法保证其逆解的存在,同时这种描述方式也缺乏空间直观性。为了解决这一问题,从机械臂自由度约束的角度出发,采用5个位姿变量描述末端连杆的位姿。由于这种方法的机械臂自由度数目和运动约束数目相同,保证了逆解的存在性。同时,这种描述方式较好的空间直观性便于利用几何法进行运动学反解,虽然未完全限制末端连杆的位姿,但没有进行约束的那个自由度为绕末端连杆坐标系接近矢量[9]的旋转运动,这种约束方式对很多应用场合下的机械臂适用,如喷涂机械臂,焊接机械臂等对末端执行器绕接近矢量方向的旋转运动没有严格要求的情况。
基于上述说明,对末端坐标系位姿进行描述时只能限制其5个方向的运动才能保证目标位姿有逆解。首先,以末端坐标系原点在基础坐标系中的坐标作为机械臂的末端位置坐标,这样限制了3个移动自由度。然后,抛弃传统的以末端坐标系相对于基础坐标系的欧拉角描述机械臂末端姿态的方式,采用末端连杆坐标系的接近矢量相对于基础坐标系的3个方向余弦角中的任意两个去描述机械臂末端姿态。3个方向余弦角变量相关,根据方向余弦角公式,其中任意一个方向余弦角可由另外两个方向余弦角求出。因此,可以用任意两个方向余弦角描述机械臂末端姿态。这样,就实现了以5个变量描述机械臂末端的位姿。位姿变量示意图如图2所示,其中,α,β,γ分别为末端坐标系接近矢量相对于基础坐标系X,Y,Z3个轴的余弦角,pn向量为末端执行器的位置坐标向量,xn,x′n为末端坐标系接近矢量。
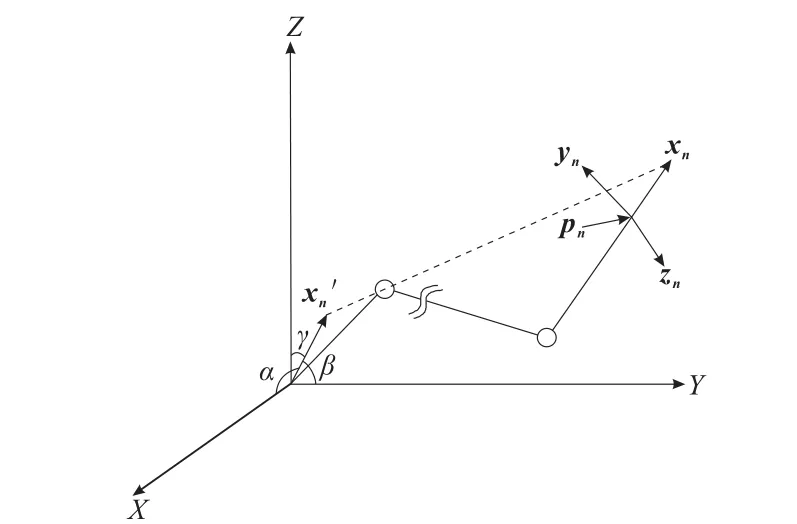
图2 位姿变量
基于上述约束自由度的思想,通过对轨迹节点上的末端坐标系原点相对于基础坐标系的3个位置坐标(px,py,pz)以及末端坐标系接近矢量相对于基础坐标系的3个方向余弦角(α,β,γ)中的任意两个所组成的五维位姿变量进行插补规划,然后利用几何法进行逆运动学求解即可得到对应的关节角空间解,且逆解一定存在。
2.2 几何法运动学逆解
机械臂各连杆的空间位置示意图如图3所示,从图中可以看出,无论5个关节角度变量取何值,连杆1、连杆2、连杆3、连杆4、连杆5的坐标系原点始终在同一平面上,该平面的位置由且仅由θ1确定。
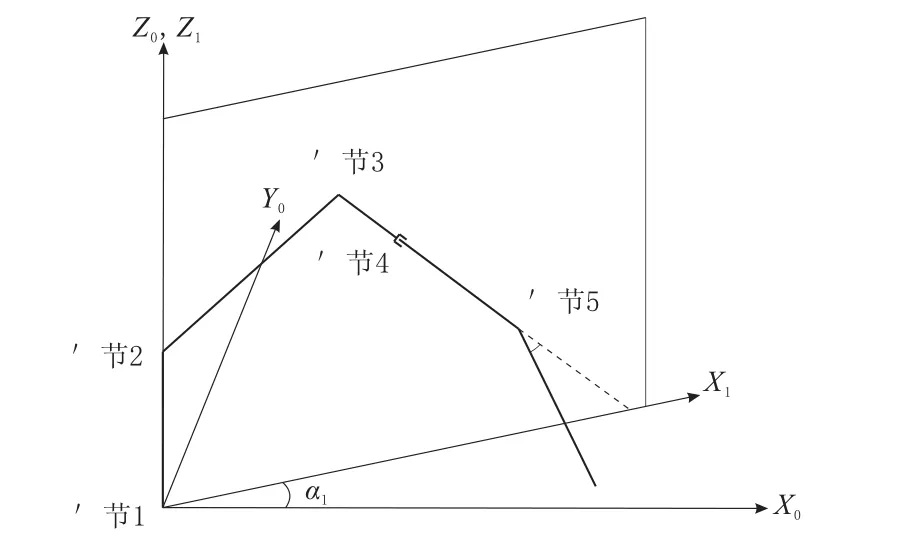
图3 连杆空间位置
由于该机械臂几何构型的特殊性,如果已知了连杆5坐标系的位置坐标以及连杆5坐标系接近矢量的方向即可方便地通过几何求解的方法求解出各个关节角变量。已知条件为连杆5坐标系全局位置坐标以及连杆5坐标系接近矢量x5(对应图1中X5Y5Z5坐标系的X轴,后面相似向量对应情况相同),具体求解流程简述如下:
a.由连杆5坐标系的位置坐标直接求解得到θ1。
b.计算连杆5坐标系在连杆1坐标系中的位置坐标,由此坐标以及连杆2、连杆3和连杆4的长度计算出θ2,θ3。
c.由θ1,θ2,θ3求出连杆4坐标系轴向量z4,由z4及x5求出z5,进而求出θ4。
d.利用连杆5坐标系轴向量x5相对于连杆4坐标系方向求解出θ5。
假设目标末端连杆位姿矩阵为:
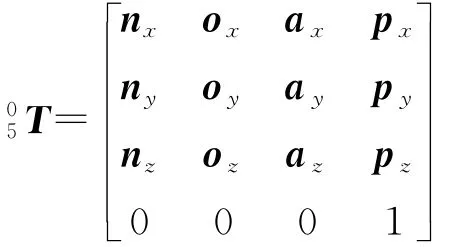
此时,p5(px,py,pz),x5(nx,ny,nz),为已知量。由p5可直接求得:
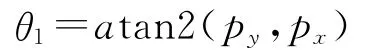
或者
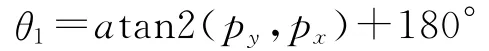
为了将后续计算转化为平面计算,求出连杆5坐标系在连杆1坐标系中的位置坐标p′5(p′x,p′y,p′z):
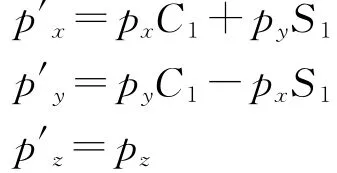
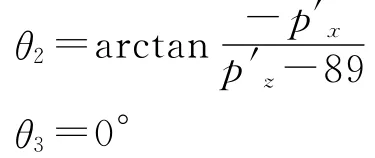

或者
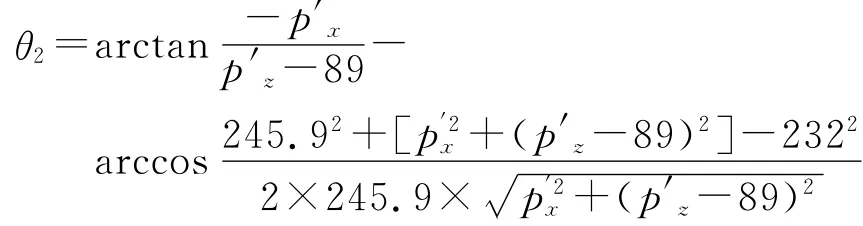
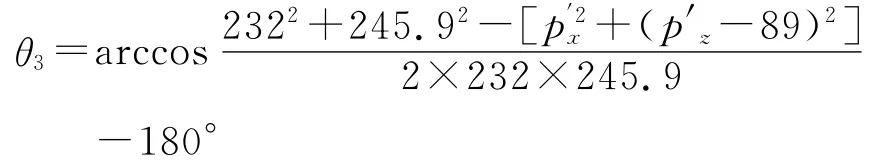
至此,已求出θ1,θ2,θ3。由此,可求出连杆4坐标系 向 量 z4(a4x,a4y,a4z)。a4x=C1S3-2;a4y=S1S3-2;a4z=C3-2。
当z4与x5平行时,可取θ4=θ5=0°。
当z4与x5不平行时,利用z5为z4与x5的公垂线求解出z5,进而确定了连杆5坐标系的完整位姿。由于z5的双向性,z5(a5x,a5y,a5z)有2组解:
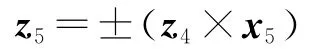
得到连杆5坐标系的完整位姿后,通过连杆5坐标系相对于连杆3坐标系、连杆4坐标系的位姿,可分别求出:
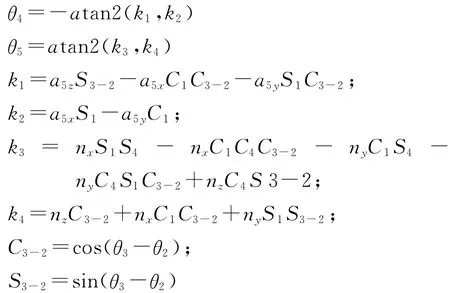
至此,5个关节角度变量完全求出,共有8组解,可以根据关节角变量取值范围以及运动连续性找出合适的惟一解。
3 仿真实验
为了验证上述算法的可行性以及正确性,对一条指定的直线轨迹进行运动追踪,用Matlab编写脚本程序进行运动规划以及运动学逆解,并通过三维图像的形式将生成轨迹与实际期望轨迹进行对比。
在该仿真实验中,以末端坐标系XhYhZh为对象进行运动规划,轨迹起始点处末端坐标系位置坐标为 (354.0,173.0,403.0),Xh轴 方 向 角 为(29.27°,68.38°,71.25°),轨迹终止点处末端坐标系位置坐标为(343.0,286.0,453.0),Xh轴方向角为(34.46°,84.19°,56.17°)。由于每个目标位姿可能对应8组逆解。因此,需要寻求合理的惟一解,可以利用关节角度变量取值范围以及运动连续性进行最优解的寻找。此处运动连续性判断公式[10]是,Δ取最小时对应的解即为最优解:
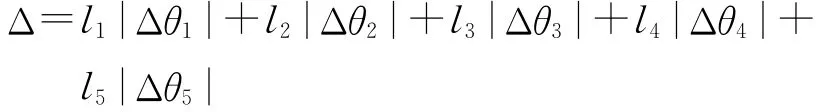
l1,l2,l3,l4,l5为加权因子,由于靠近基座的关节变化对末端影响较大。因此,对应的加权因子也取较大值,这里l1=l2=l3=1,l4=l5=0.5。
下面对位置坐标以及方向角分别进行线性插补。对于方向角的坐标,只对方向向量与X,Y轴的余弦角α,β进行线性插补,方向向量与Z轴的余弦角γ由α,β计算得出。插补后位置坐标ph(pxh,pyh,pzh)和Xh轴方向角(αh,βh,γh)为:
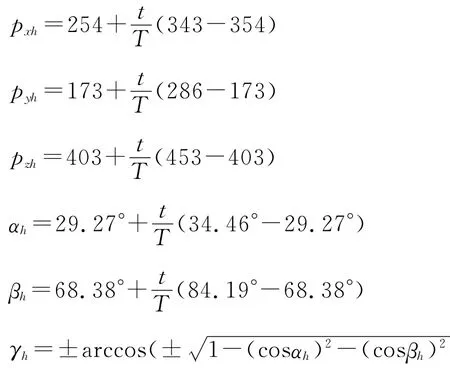
T为运动周期,令T=10s,γh取跟前一次插补最接近的值。为了方便逆运动学求解的进行,需求出关节5坐标系对应的位置坐标p5(px,py,pz),以及连杆5方向向量x5(nx,ny,nz)。
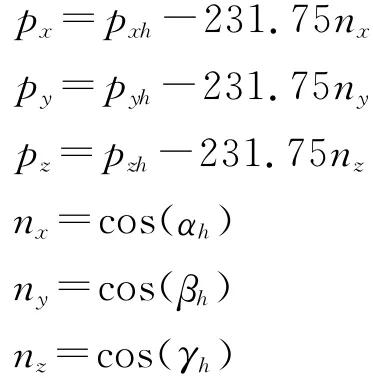
位置追踪结果如图4所示,机械臂整体姿态如图5所示,求解出的关节角度值如图6所示。
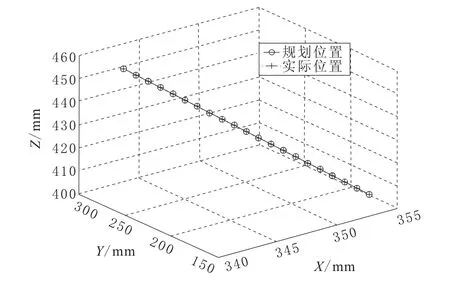
图4 位置追踪结果
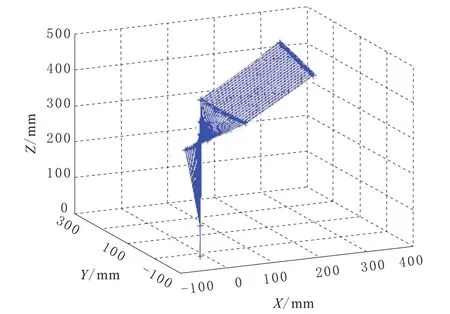
图5 机械臂整体姿态
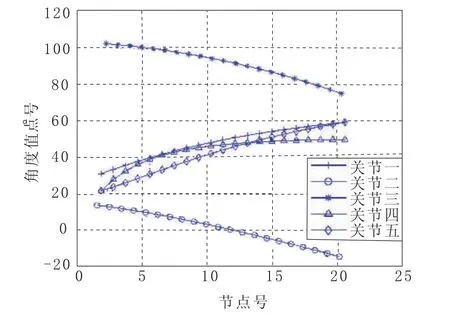
图6 关节角度变化曲线
从仿真结果可以看出,仿真生成位置与期望位置吻合程度较好,证明了该算法的可行性与精确性,从理论角度来看没有误差。同时,通过运动学逆解求出的关节空间解在关节变量可达空间内,且无突变,即关节运动较为平滑。
4 结束语
针对五自由度机械臂因自由度不足而导致的轨迹规划所产生的目标位姿不存在运动学逆解的问题,提出了一种在轨迹规划阶段新的末端位姿描述方法,并结合机械臂本身自由度少、结构简单的优势,采用几何法进行逆运动学求解,求解过程较为简单,且不存在理论误差。在实际实施过程中,由于该算法计算复杂度低。因此,利用计算机编程的方式实现该算法十分方便,实时性好。虽然该算法针对特定的机械臂构型提出,但这种采用约束自由度的思想进行末端位姿描述,并采用几何法求解目标末端位姿对应的关节角空间解的思路,对于一般的五自由度机械臂有一定的通用性。
[1] Assal S F M,Watanabe K,Izumi K.Neural network learning from hint for the inverse kinematics Problem of redundant arm subject to joint limits[A].IEEE/RSJ International Conference on Intelligence Robots and System[C].Piscataway,NJ,USA:IEEE,2005.1477-1482.
[2] Nearchou A C.Solving the inverse kinematics problem of redundant robots operating in complex environments via a modified genetic algorithm[J].Mechanism and Machine Theory,1998,33(3):273-292.
[3] Oyama E,Agah A,MacDorman K F,et al.A modular neural network architecture for inverse kinematics model learning[J].Neurocomputing,2001,(38-40):797-805.
[4] Xia Y,Wang J.A dual neural network for kinematic control of redundant robot manipulators[A].IEEE Transactions on Systems,Man,and Cybernetics,Part B[C].2001,31(1):147-154.
[5] Mohamed H A F,Yahya S,Moghavvemi M,et al.A new inverse kinematics method for three dimensional redundant manipulators[A].ICCAS-SICE[C].Piscataway,NJ,USA:IEEE,2009.1557-1562.
[6] Song D H,Jung S.Geometrical analysis of inverse kinematics solutions and fuzzy control of humanoid robot arm under kinematics constrains[A].IEEE International Conferrence on Mechatronics and Automation[C].Piscataway,NJ,USA:IEEE,2007.1178-1183.
[7] Yahya S,Mohamed H A F,Moghavvemi M,et al.A new geometrical inverse kinematics method for planar hyper redundant manipulator[A].Innovative Technologies in Intelligent Systems and Industrial Applications[C].Piscataway,NJ,USA:IEEE,2009.20-22.
[8] Li S,Wang Y Q,Chen Q W,et al.A new geometrical method for the inverse kinematics of the hyper-redundant manipulators[A].IEEE International Conferrence on Robotics and Biomimetics[C].Piscataway,NJ,USA:IEEE,2006.1356-1359.
[9] 熊有伦.机器人学,2版[M].北京:机械工业出版社,1993.
[10] 陈 鹏,刘 璐,余 飞,等.一种仿人机械臂的运动学逆解的几何求解方法[J].机器人,2012,34(2):211-216.

