New Exact Solutions of the Generalized Davey-Stewartson and Mikhailov-Shabat Equations
LAN Tianzhu, XU Yancong, WANG Liangbin
(School of Science, Hangzhou Normal University, Hangzhou 310036, China)
1 Introduction
In recent years, many kinds of coherent structures and nonlinear waves of the nonlinear partial differential equations(NPDEs) have more and more important applications in lasers, hydrodynamics, plasmas and gas-discharge systems, etc. How to explain the rationality and seek their exact solutions of partial differential equations attracted research interest of many mathematicians and physicists. However, it is not easy to find exact traveling wave solutions of different models, several analytical methods have been developed in order to obtain wave solutions of reaction-diffusion or dissipative systems, such as the inverse scattering method[1], the Hirota’s method[2], the F-expansion method[3], the sine-cosine method[4], the Jacobi elliptic function method[5], the variable separation method[6]and tanh-function method[7]. Those exact solutions will help us to know about the dynamics of models, also provide a starting solution when we carry out the numerical simulations by using the software AUTO07[8].
The first integral method was first proposed by Feng[9]in solving Burgers-KdV equation which is based on the ring theory of commutative algebra. This method was further developed by some other mathematicians[10-12], and see references cited therein.
In this work, we aim to get more general exact traveling wave solutions or steady state solutions ( if we take the velocityc=0) to generalized two-dimensional Davey-Stewartson and Mikhailov-Shabat equations by using the first integral method, which generalized the solutions given in [7,13].
The rest of the paper is organized as follows. In section 2, we will introduce the first integral method for solving exact solutions of nonlinear partial differential equations. In section 3 and section 4, we will obtain in details some general complex exact solutions of the generalized Davey-Stewartson equation and the generalized Mikhailov-Shabat (MS) equation by using the first integral technique. Finally, some conclusions are given.
2 The first integral method
Consider the following nonlinear partial differential equation
F(u,ux,ut,uxx,uxt,…)=0,
(1)
whereu(x,t) is the solution of (1). By using the transformationu(x,t)=f(ξ),whereξ=x-ct,cis the velocity of wave. As we know, ifc≠0, the solution is a traveling wave solution; ifc=0, it is a steady state solution. Then we obtain
(2)
Then it is easy to change the NPDE (1) into a nonlinear ordinary differential equation(ODE)
G(f,fξ,fξξ,…)=0.
(3)
Next, we introduce a new independent variable
X(ξ)=f(ξ),Y(ξ)=fξ(ξ),
(4)
which lead a system of ODEs
Xξ(ξ)=Y(ξ),Yξ(ξ)=F(X(ξ),Y(ξ)).
(5)
According to the qualitative theory of differential equation, if we can get the first integrals to Eq.(5), then the general solution to Eq.(5) can be solved directly. However, frankly speaking, it is really difficult for us to realize this even for one first integral, because for a given plane autonomous system, there is no systematic theory that can tell us how to obtain its first integrals, nor is there a logical way of telling us what these first integrals are. We will apply the Division Theorem in Feng[9]to obtain one first integral to Eq.(5) which reduces Eq.(3) to a first order integrable ordinary differential equation. An exact solution to Eq.(1) is then obtained by solving this equation. Now let us recall the Division Theorem as follows.
DivisionTheoremSuppose thatP(w,z) andQ(w,z) are polynomials inC[w,z] andP(w,z) is irreducible inC[w,z]. IfQ(w,z) vanishes at all zero points ofP(w,z), then there exists a polynomialG(w,z) inC[w,z] such thatQ(w,z)=P(w,z)G(w,z).
3 Generalized Davey-Stewartson equation
As we know, the nonlinear partial differential equations with constant coefficients in [13] can be written as
(6)
whereP,Ai,Bi,Ci(i=1,2) are real constants andP≠0,C1≠0,C2≠0. Eqs.(6) are a class of physically important equations. In fact, if we take
then Eqs.(6) represent the Davey-Stewartson equation[14]

If one takes
n=n(x,t),P=1,A1=0,B1=-2λ,C1=2,A2=-1,B2=0,C2=-1.
Then Eqs.(6) become the generalized Zakharrov equation[15]

Supposeu(x,y,t) is a complex solution of Eqs.(6), we make the transformation
u(x,y,t)=eiθf(ξ),n(x,y,t)=g(ξ),
whereθ=αx+βy+γt,ξ=ax+by+ct, we have a relationc+2Paα+2bPA1β=0, then Eqs.(6) can be reduced to the following system of ordinary differential equations
(-γ-α2P-PA1β2)f(ξ)+(Pa2+A1b2P)f″(ξ)+B1f3(ξ)+C1f(ξ)g(ξ)=0,
(7)
(A2c2+a2-B2b2)g″(ξ)+a2C2(f2(ξ))″=0.
(8)
Integrating Eq.(8) twice with respect toξ, we get
(9)
whereRis the second integration constant and the first one is taken to zero. Inserting (9) into (7), we yield
Using (4) and (5), we get

(10)
(11)
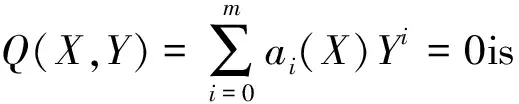
(12)
whereai(X)(i=0,1,…,n) are polynomials ofxandam(X)≠0. Eq.(12) is called the first integral to (10), (11). Due to the Division Theorem, there is a polynomialg(X)+h(X)Y, such that
(13)
We assume them=1 in (12), by comparing with the coefficients ofYion both sides of (13), we have
(14)
(15)
(16)
From (14) we deducea1(X) is a constant andh(X)=0. For simplicity, takea1(X)=1. Balancing the degrees ofa0(X) andg(X), we conclude that degg(X)=1. Supposeg(X)=S1X+W0, then we can obtain
(17)
whereS0is an arbitrary integration constant. Substitutingg(X) anda0(X) into (16) and setting all the coefficients of powersXto be zero, it follows
(18)
(19)
Using (12) and (17), we have
(20)
Combining (10), (12), (18) and (20), we can get the exact solutions to Eq.(11) and the exact solutions to the generalized nonlinear partial differential equations with constant coefficients.
(i) IfS0>0, we can get

(ii) IfS0<0, it follows that

(ax+by+ct)+ξ0].
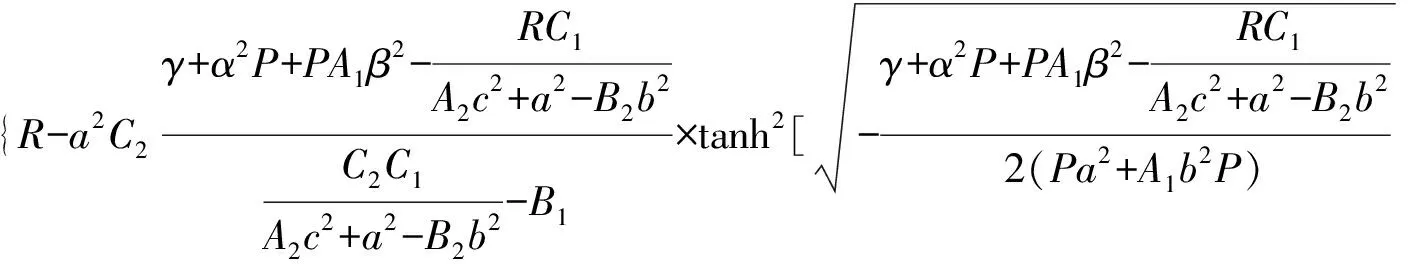
Combining (10), (12), (19) and (20), we can get the exact solutions to Eq.(11) and the exact solutions to the generalized nonlinear partial differential equations with constant coefficients.
(iii) IfS0<0, we can obtain

(iv) IfS0>0, we get

(ax+by+ct)+ξ0].
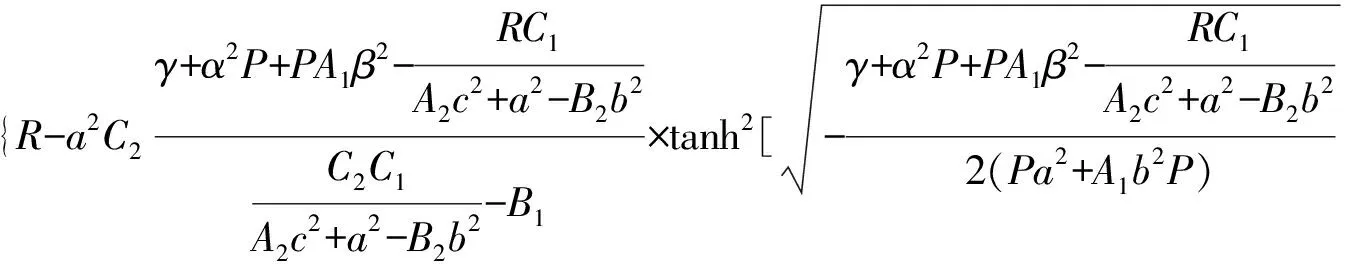
Note that, here we obtain some more general exact traveling wave solutions with the form of “tanh” and “tan” by the variablesx,y,t. However, there are only simple traveling wave solutions with the variablesx,tin [13], which cannot reflect completely the dynamics of Davey-Stewartson equation.
4 Generalized Mikhailov-Shabat(MS) equation
Now we consider the generalized Mikhailov-Shabat(MS) equation in [7,16] with the following form
(21)
If we take the following new transformation
(22)
then Eqs.(21) become
(23)
Supposeu(x,t),v(x,t) are solutions of Eqs.(23), we takeu(x,t)=f(ξ),v(x,t)=g(ξ),ξ=x-ct, then Eqs.(23) is reduced to
-cg′(ξ)-2f″(ξ)+2f(ξ)g′(ξ)+16βf3(ξ)=0,
(24)
-2cf′(ξ)-g″(ξ)-4f(ξ)f′(ξ)=0,
(25)
Integrating Eq.(25) with respect toξ, we get
g′(ξ)=-2cf(ξ)-2f2(ξ)+c1,
(26)
wherec1is an integral constant.


(27)
(28)

(29)
whereai(X)(i=0,1,2,…,m) are polynomials ofXandam(X)≠0. Eq.(29) is called the first integral to (28). Due to the Division Theory, there exists a polynomialg(X)+h(X)Yin the complex domain, such that
(30)
Assumingm=1 in (29), by equating the coefficients ofYi(i=0,1,2) on both sides of (30), one obtains
(31)
(32)
(33)

(34)
(35)
Using (34) and (29), we get
(36)
(i) Ifc2-6(c2+c1)(4β-1)<0, by (36), we can obtain the exact solutions to (23) as follow

whereξ0is an arbitrary constant. Then we obtain the exact solutions to (21) as follow


(ii) Ifc2-6(c2+c1)(4β-1)>0, by (36), we can obtain the exact solutions to (23) as follow

whereξ0is a constant. Then we obtain the exact solutions to (21) as follow


Combining (35) and (29), we can get
(37)
(iii) Ifc2-6(c2+c1)(4β-1)<0, by (37), we can obtain the exact solutions to (23) as follow

whereξ0is a constant. Then the following exact solutions to (21) is
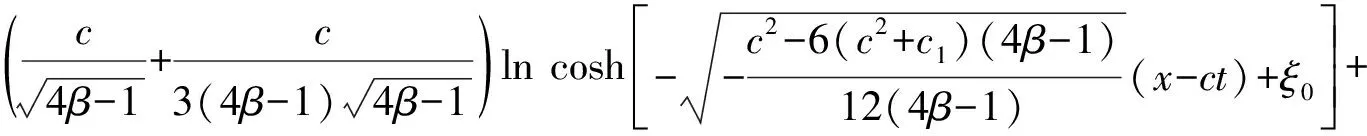
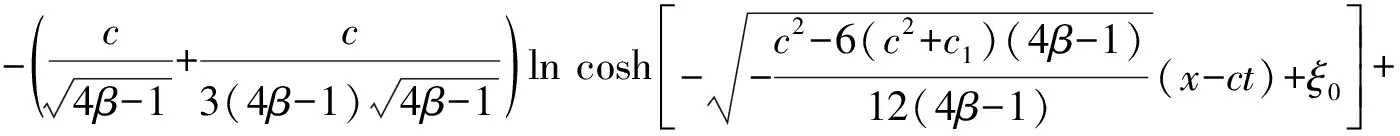
(iv) Ifc2-6(c2+c1)(4β-1)>0, by (37), we can obtain the exact solutions to (23) as follow

whereξ0is an arbitrary constant. Then we obtain the exact solutions to (21)



Obviously, we obtain several exact traveling wave solutions of general MS equation which is different from the equation in [7,16].
RemarkNote that, here we only derived some general solutions with many undefined parameters for the corresponding equations, if we take concrete values of parameters, then we can obtain more explicit solutions, including the numerical simulations.
ConclusionMany biological, physical or chemical phenomena can be modeled by nonlinear partial differential equations, including reaction-diffusion systems and dissipative systems. In order to investigate their dynamical behaviors, we sometimes need to know about the situation of their own solutions. In this paper, the first integral method was applied successfully for obtaining the real or complex exact solutions of the generalized two-dimensional Davey-Stewartson equation and Mikhailov-Shabat(MS) equation. Thus, we conclude that the proposed method can be extended to solve the exact solutions of more nonlinear partial differential equations.
:
[1] Ablowitz M J, Claekson P A. Solitons, nonlinear evolution equation and inverse scattering[M]. Cambridge: Cambridge University Press,1991.
[2] Gu C H. Soliton theory and its application[M].Hangzhou: Zhejiang Science and Technology Press,1990.
[3] Wang M L, Li X Z. Applications of F-expansion to periodic wave solutions for a new Hamiltonian amplitude equation[J]. Chaos, Solitons and Fractals,2005,24(5):1257-1268.
[4] Wazwaz A M. A Sine-Cosine method for handling nonlinear wave equations[J].Mathematical and Computer Modelling,2004,40:499-508.
[5] Fu Z T, Liu S K, Liu S D,etal. The JEFE method and periodic solutions of two kinds of nonlinear wave equations[J]. Communication in Nonlinear Science and Numerical Simulation,2003,8(2):67-75.
[6] Cao C W, Wu Y T, Geng X G. Relation between the Kadomtsev-Petviashvili equation and the Confocal involutive system[J].J Math Phys,1999,40:3948-3970.
[7] Sirendaoreji. New exact travelling wave solutions to three nonlinear evolution equations[J].Appl Math J Chin Univ Ser B,2004,19:178-186.
[8] Sandstede B, Xu Y C. Snakes and isolas in non-reversible conservative systems[J].Dynamical Systems,2012,27(3):317-329.
[9] Feng Z S. The first integral method to study the Burgers-KdV equation[J]. J Phys A:Math Gen,2002,35(2):343-349.
[10] Deng X J. Travelling wave solutions for the generalized Burgers-Huxley equation[J]. Appl Math Comput,2008,204(15):733-737.
[11] El-Ganaini S I. Travelling wave solutions of the Zakharov-Kuznetsov equation in plasmas with power law nonlinearity[J]. Int J Contemp Math Sci,2011,6(48):2353-2366.
[12] El-Ganaini S I. Travelling wave solutions to the generalized Pochhammer-Chree (PC) equations using the first integral method[J]. Math Problems Eng,2011,10:629-760.
[13] El-Wakil S A, Abdou M A. New exact travelling wave solutions using modified extended tanh-function method[J]. Chaos, Solitons and Fractals,2007,31(4):840-852.
[14] Davey A, Stewartson K. On three-dimensional packets of surface waves[J]. Proc R Soc Lond A,1974,338(1613):101-110.
[15] Malomed B, Anderson D, Lisak M,etal. Dynamics of solitary waves in the Zakharov model equations[J]. Phys Rev E,1997,55:962-968.
[16] Estevez P G, Gordoa P R, Alonso L M,etal. Modified singular manifold expansion: application to the Boussinesq and Mikhailov-Shabat systems[J]. J Phys A:Math Gen,1993,26(8):1915-1925.

