相关Yetter-Drinfeld模范畴上的(D,H)-Hopf模

胡希能,李文强,李金其

(浙江师范大学数理与信息工程学院,浙江 金华321004)

1983年,Doi在文[1]中由右A-模余代数C得到了右(C,A)-Hopf模, 当存在右A-模同态ψ:C→A, 且满足εψ=ε时, 所有的右(C,A)-Hopf模作为A-模都是投射的, 最后给出了(C,A)-Hopf 模同构定理.

1998年,Doi在文[2]中给出了Yetter-Drinfeld Hopf代数的一般介绍, 并且给出了Yetter-Drinfeld Hopf代数上的相关Hopf模基本结构定理.

2013年,Heckenberger在文[3]中给出了相关Yetter-Drinfeld模范畴的描述.论文由此相关Yetter-Drinfeld模范畴诱导出新的范畴把文[1]的部分结论推广到这个诱导的范畴上, 改进了文[4]的结论.

定义1[3]设B，C是有双射对极的Hopf代数,α:B→C是Hopf代数同态, 记下面的张量范畴为, 其对象M是右B-模和右C-余模, 且对任意b∈B,m∈M满足

(m〈0〉b1)⊗m〈1〉α(b2)=(mb2)〈0〉⊗α(b1)(mb2)〈1〉，

(1)

其中M的右B-模作用为“mb”,右C-余模作用为⊗m〈1〉.

式(1)等价于

(2)

两个对象的态射为右B-模同态和右C-余模同态.

定义2设B，C是有双射对极的Hopf代数,α:B→C是Hopf代数同态,L是的对象, 称L为上的双代数, 若对任意x,y∈L,b∈B满足:

2)L是B-模代数,即

(xy)←α(b)=(x←α(b1))(y←α(b2)),1L←α(b)=1LεB(b)；

3)L是B-模余代数,即

Δ(x←α(b))=(x1←α(b1))⊗(x2←α(b2)),εL(x←α(b))=εL(x)εB(b)；

4)L是C-余模代数,即

5)L是C-余模余代数,即

若还存在idL的卷积逆S,则称L为上的Hopf代数.S是中的态射,故S是右C-模同态,右B-模同态和右C-余模同态,即

文[2]中证明了S是反代数同态和反余代数同态,即

此处采用如下记号,对任意的向量空间V,

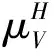
定义3设H,D是上的Hopf代数,D是左H-模,称D是上的左H-模余代数,若对任意的h∈H,d∈D满足:

(hd)←α(b)=(h←α(b1))(d←α(b2))；

定义4设H,D是上的Hopf代数,且D是上的左H-模余代数,M是上的对象,同时M是左H-模和左D-余模,称M是上的左(D,H)-Hopf模,若对任意的m∈M,b∈B,h∈H满足:

1)M是(D,H)-Hopf模,即

(hm)←α(b)=(h←α(b1))(m←α(b2))；

m-1〈0〉⊗m0〈0〉⊗m-1〈1〉m0〈1〉=m〈0〉-1⊗m〈0〉0⊗m〈1〉；

例1设H,D是上的Hopf代数,且D是上的左H-模余代数,则D本身是上的左(D,H)-Hopf模.

例2设H,D是上的Hopf代数,且D是上的左H-模余代数,M是上的左(D,H)-Hopf模,则D⊗M是上的(D,H)-Hopf模.其中D⊗M的模作用、余模作用分别定义如下.

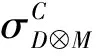
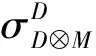
证明1)验证D⊗M是(D,H)-Hopf模,对任意h∈H,d∈D,m∈M,

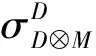
(d←α(b1))1⊗(d←α(b1))2⊗(m←α(b2))=

(d1←α(b1))⊗(d2←α(b2))⊗(m←α(b3))=(d1←α(b1))⊗((d2⊗m)←α(b2)).

(hd←α(b1))⊗(m←α(b2))=(h←α(b1))(d←α(b2))⊗(m←α(b3)).

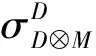
(hd)〈0〉⊗m〈0〉⊗(hd)〈1〉m〈1〉=h〈0〉d〈0〉⊗m〈0〉⊗h〈1〉d〈1〉m〈1〉.

故D⊗M是上的左(D,H)-Hopf模.

例3设H,D是上的Hopf代数,且D是上的左H-模余代数,M是上的左(D,H)-Hopf模,则H⊗M是上的左(D,H)-Hopf模.其中H⊗M的右B-模作用、右C-余模作用定义同例2,左H-模作用、左D-余模作用定义如下.

注由上述例子可知H⊗D,D⊗D是上的(D,H)-Hopf模.

定理1设H,D是上的Hopf代数,D是上的左H-模余代数,若存在上的左H-模同态φ:D→H,且φ是余代数同态,则上的任意左(D,H)-Hopf模作为左H-模都是投射的.

证明设M是上的任意左(D,H)-Hopf模,定义λ:M→H⊗M为

λ(m)=φ(m-1)1⊗S(φ(m-1)2)m0.

2)验证λ是左H-模同态,因为对任意h∈H,m∈M,

φ(h11m-1〈0〉1〈0〉)⊗Sφ((h12←m-1〈0〉1〈1〉)m-1〈0〉2)(h2←m-1〈1〉)m0=

h11φ(m-1〈0〉1〈0〉)⊗Sφ((h12←m-1〈0〉1〈1〉)φ(m-1〈0〉2))(h2←m-1〈1〉)m0=

h11φ(m-1〈0〉1〈0〉)⊗Sφ(m-1〈0〉2〈0〉)((S(h12)←m-1〈0〉1〈1〉)←m-1〈0〉2〈1〉)(h2←m-1〈1〉)m0=

hφ(m-1〈0〉〈0〉1)⊗Sφ(m-1〈0〉〈0〉2)(1H←m-1〈0〉〈1〉m-1〈1〉)m0=

hφ(m-1〈0〉1)⊗Sφ(m-1〈0〉2)(1H←m-1〈1〉1m-1〈1〉2)m0=

hφ(m-11〈0〉)⊗Sφ(m-12〈0〉)(1H←m-11〈1〉m-12〈1〉)m0=

hφ(m-11)⊗Sφ(m-12)m0=(I⊗λ)(M⊗I)(h⊗m).

3)验证λ是右B-模同态,因为对任意b∈B,m∈M,

φ(m-11←α(b11))⊗Sφ(m-12←α(b12))(m0←α(b2))=

(φ(m-11)←α(b11))⊗(Sφ(m-12)←α(b12))(m0←α(b2))=

4)验证λ是右C-余模同态,因为对任意m∈M,

φ(m-11〈0〉)⊗Sφ(m-12)〈0〉m0〈0〉⊗φ(m-11〈1〉Sφ(m-12)〈1〉)m0〈1〉=

φ(m-1〈0〉1)⊗Sφ(m-1〈0〉2)m0〈0〉⊗m-1〈1〉m0〈1〉=

因此M在上作为左H-模是投射的.

D是上的左H-模余代数,H+是映射ε:H→K的核,则H+D是D的余理想.因而有唯一的余代数结构使得投射是余代数同态.

设M是上的左(D,H)-Hopf模,P诱导了M的左余模结构:⊗⊗M,由于H+M是M的子余模，故有唯一的余模结构使得自然同态是左余模同态,即⊗π)(P⊗且对任意h∈H,m∈M,π(hm)=ε(h)π(m).

命题1设H,D是上的Hopf代数,且D是上的左H-模余代数,M是上的左(D,H)-Hopf模,则是的对象.

证明对任意m∈M,h∈H+,(hm)b=(h←b1)(m←α(b2)),而(m←α(b2))∈M,ε(hb1)=ε(h)ε(b1)=0,所以h←b1∈H+,(hm)b∈H+M,H+M是M的右B-子模.

定理2设H,D是上的Hopf代数,D是上的左H-模余代数,M是上的左(D,H)-Hopf模,若有左H-模同态φ:D→H,且φ是余代数同态,则对所有上的(D,H)-Hopf模M,F:M→D□是上的同构.

Q(hm)=Sφ(h1m-1〈0〉)((h2←m-1〈1〉)m0)=S(h1φ(m-1〈0〉))((h2←m-1〈1〉)m0)=

Sφ(m-1〈0〉)〈0〉(S(h1)←φ(m-1〈0〉)〈1〉)(h2←m-1〈1〉)m0=

Sφ(m-1〈0〉)〈0〉(ε(h)←φ(m-1〈0〉)〈1〉m-1〈1〉)m0=0.

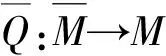
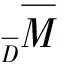
1)验证GF=idM.因为对∀m∈M,

GF(m)=G(m-1⊗π(m0))=φ(m-1)Q(m0)=φ(m-1)Sφ(m0-1)m00=φ(m-11)Sφ(m-12)m0=

φ(m-1)1Sφ(m-1)2m0=εφ(m-1)m0=ε(m-1)m0=m.

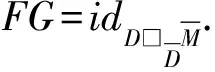
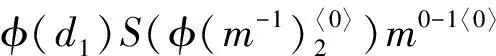
φ(d)Sφ(m-1)2εD(φ(m-1)1)m0-1⊗π(m00)=φ(d)Sφ(m-1)m0-1⊗π(m00)=

φ(d)Sφ((m-1)1)(m-1)2⊗π(m0)=φ(d)Q0(m-1)⊗π(m0).

φ(D)Q0(m-1)⊗π(m0)=d⊗π(m).

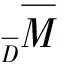
[1] Doi Y. On the structure of relative Hopf modules[J]. Communications in Algebra,1983,11(3):243-255.

[2] Doi Y. Hopf modules in Yetter-Drinfeld categories[J]. Communications in Algebra,1998,26(9):3057-3070.

[3] Heckenberger I，Schneider H J. Yetter-Drinfeld modules over bosonizations of dually paired Hopf algebras[J]. Advances in Mathematics,2013,244:354-394.

[4]落金枝，李强．相关Yetter-Drinfeld Hopf代数上的相关Hopf模结构定理[J]．数学学报，2011，54(3)：483-494．