三维Hom－Leibniz超代数的分类

马凤敏，张永平，董 蕾，张庆成

（1.河北工业职业技术学院基础部，河北 石家庄 050000；2.沈阳化工学院数学系，辽宁 沈阳 110142；3.东北师范大学数学与统计学院，吉林 长春 130024）

Leibniz代数最早是由A.Bloch在文献［1］中涉及的，当时称为D－代数，直到20世纪90年代，J.L.Loday在研究不满足交错性的广义李代数时，正式提出这个概念［2］.对于非李代数的Leibniz代数的研究，一直是许多学者的努力方向，在非李代数的Leibniz代数分类问题上，已经完成了对二维、三维以及四维幂零的分类［3］，在Leibniz代数其他方面的研究主要集中在关于同调问题等抽象理论上［4］.

代数形变理论最早由 M.Gerstenhaber提出［5］，Hom－代数是代数形变理论中的一类，文献［6－9］引入了Hom－代数的概念，并进行了系统的研究.对Hom－代数的分类，也是研究的一个重要内容，本文在对三维非李代数的Leibniz超代数的分类基础上［10］，研究三维非李超代数的Hom－Leibniz超代数的分类.通过偶自同态定义，运用待定系数法，得到系数的矩阵乘法表.

1 Hom－Leibniz超代数

定义1.1［1］设L是一个向量超空间：［·，·］是L×L→L的一个双线性映射，α是L→L的一个超空间偶自同态映射，满足：

则称（L，［·，·］，α）是一个 Hom－Leibniz超代数.

定理1.1 若（L，［·，·］）是一个Leibniz超代数，α：L→L是一个偶的Leibniz超代数的同态映射，则（L，［·，·］α，α）构成一个 Hom－Leibniz超代数，其中［·，·］α＝［α（x），α（y）］.

证明 显然α关于括积［·，·］α构成超代数间的同态映射，我们只需证明∀x，y，z∈L，满足Hom－Leibniz超等式.

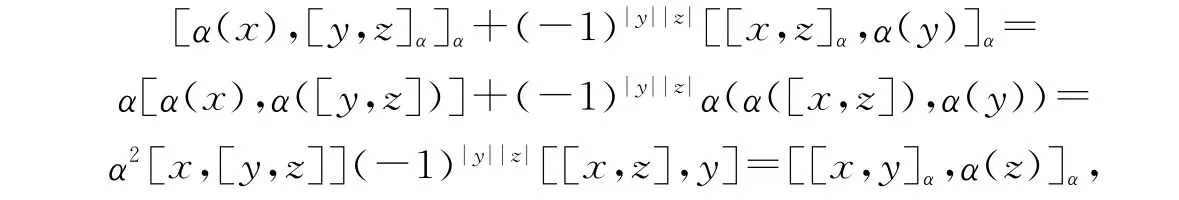
则（L，［·，·］α，α）构成一个 Hom－Leibniz超代数.

设（L，［·，·］）是一个Leibniz超代数，α是L的一个偶的自同态映射，即

设e0，e1，e2是L 的齐次基，则

利用

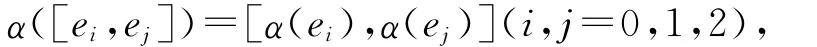
确定α（e0），α（e1），α（e2）的表达系数Lkl，k＝0，1，2；j＝1，2，3.从而确定偶自同态α的表示矩阵

2 Hom－Leibniz超代数的分类

利用文献［10］中三维Leibniz超代数的分类结果，应用定理1.1知，当α是Leibniz超代数L的一个偶自同态时，（L，［·，·］α，α）构成一个 Hom－Leibniz超代数.因此，我们可以通过待定系数法，对偶自同态α进行分类，从而完成对Hom－Leibniz超代数的分类.

证明 应用文献［10］中分类的结果.

表示成矩阵为

对应的矩阵为：

对应的矩阵为：

由方程的对称性，可以得到L01＝L11，L02＝L12或L01＝L12，L02＝L11.

当k＝0时，

① 当L01＝L11，L02＝L12时，得＋＝0，即L01＝L11＝L02＝L12＝L23＝0.

② 当L01＝L12，L02＝L11时，L01L02＋L02L01＝0，则L01L02＝0.

当k≠0时，

当L01＝L12，L02＝L11时，

即当k＝0时，

对应的矩阵为：

当k≠0时，

对应的矩阵为：

对应的矩阵为：

对应的矩阵为：

解上述方程组，当k≠0时，

对应的矩阵为：

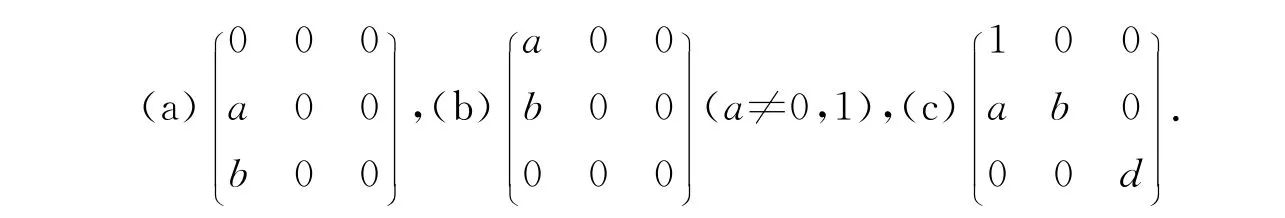
当k＝0时，

对应的矩阵为：

对应的矩阵为：

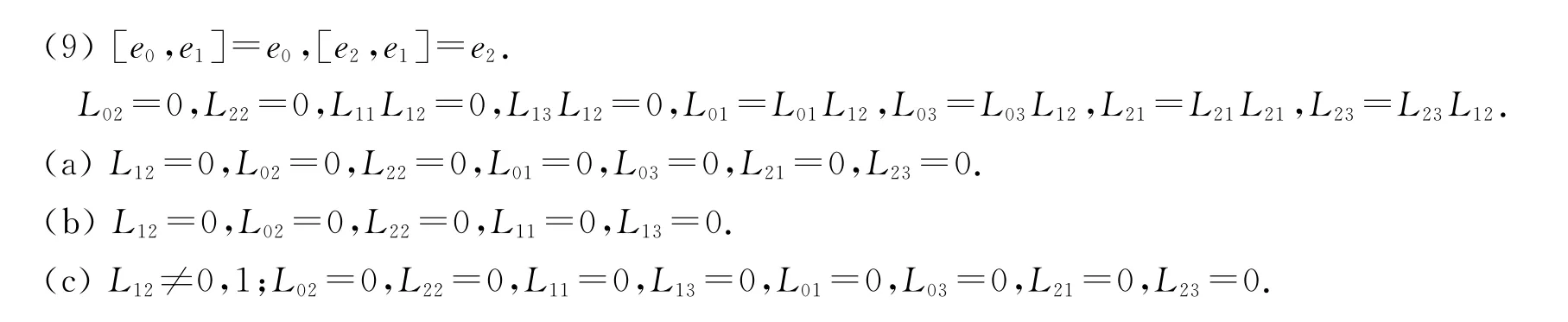
对应的矩阵为：

对应的矩阵为：

解上述方程组，当k＝0时，

对应的矩阵为：

当k＝1时，无解.

当k≠0，1时，

对应的矩阵为：

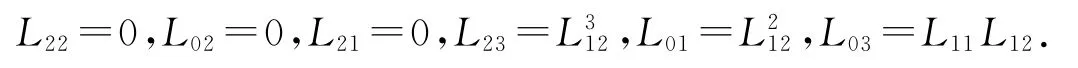
对应的矩阵为

（13）［e1，e2］＝e0＋e1，［e0，e2］＝ke1.

当k＝0时，L01＋L11＝L12L23，L02＋L12＝L12L23，L03＋L13＝0，L02L23＝0.

对应的矩阵为：

当k≠0时，L13＝0，L03＝0，L01＋L11＝L12L23，L02＋L12＝L12L23＋kL11L23，kL11＝L02L23，L02L23＋kL01L23＝kL12.

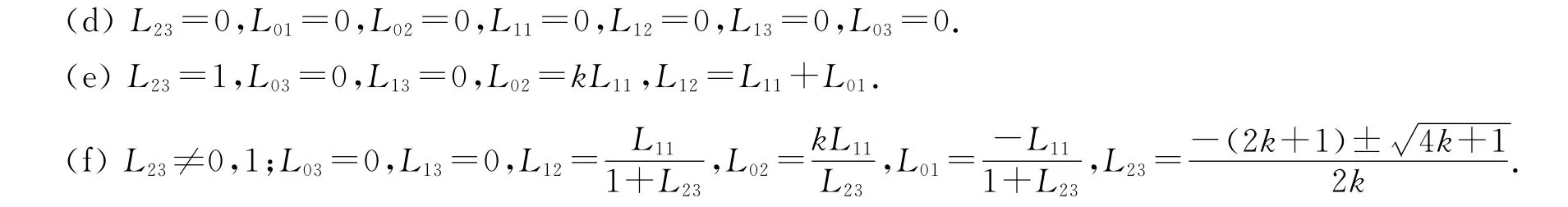
对应的矩阵为：

应用类似的方法可得下列结果：

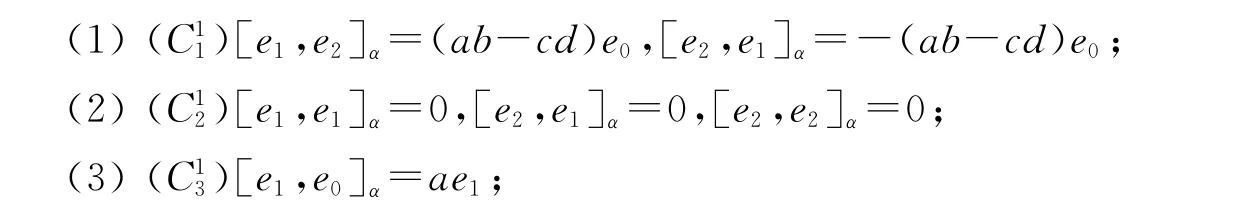
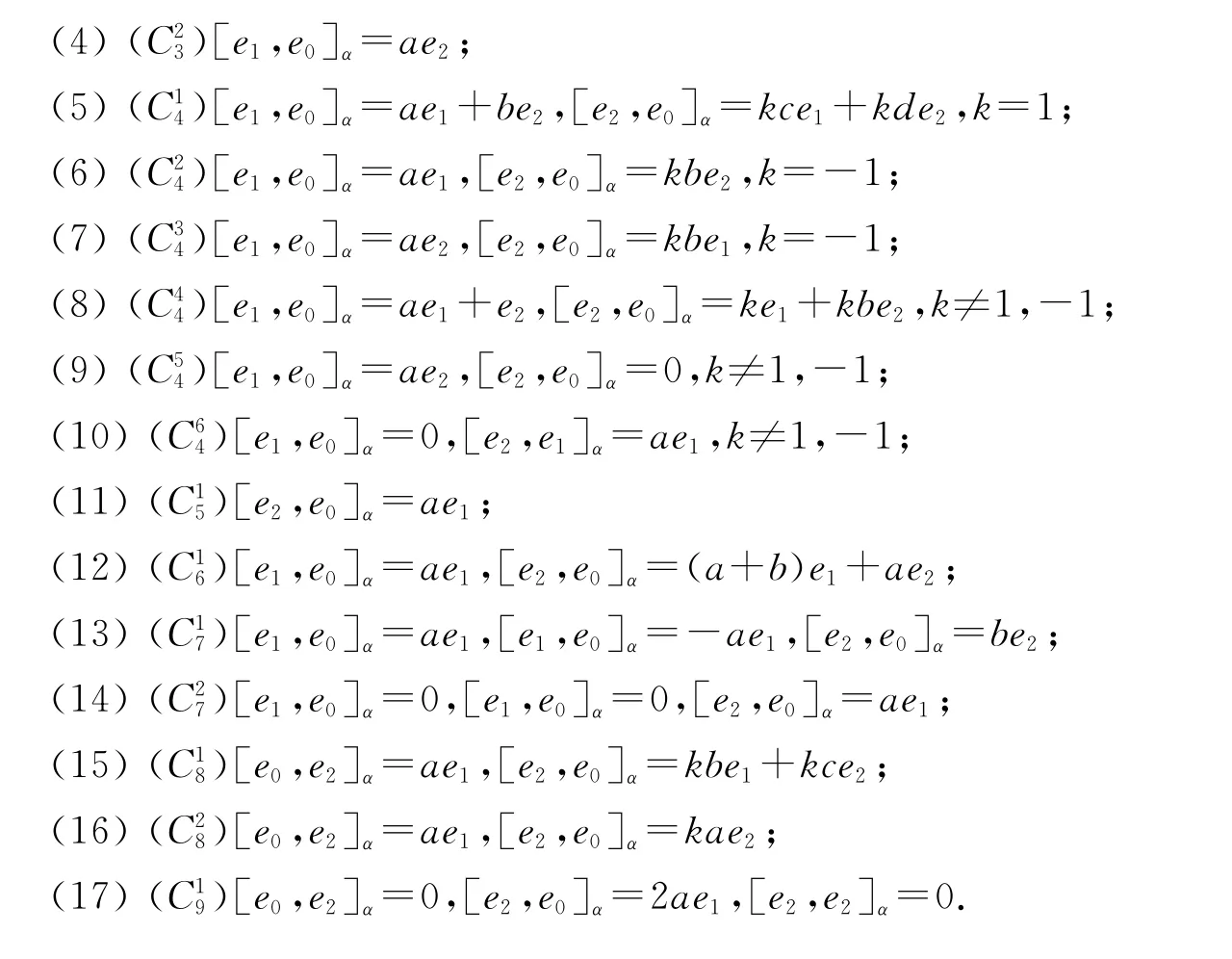
［1］BLOCH A.On a generalization of Lie algebra［J］.Math IUSSR Doklady，1965，163（3）：471－473.

［2］LODAY J L.Une version non commutative des algebras de Lie：les algebra de Leibniz［J］.Enseign Math Ann，1993，296（1）：139－158.

［3］蒋启芬.三维Leibniz代数的分类［J］.数学研究与评论，2007，27（4）：677－686.

［4］刘东.无限维Lie代数和Leibniz代数［D］.上海：华东师范大学，2004.

［5］GERSTENHABER M.On the deformation of rings and algebras［J］.Ann Math，1964，79（1）：59－103.

［6］LARSSON D，SILRESTROV S D.Quasi－Hom－Lie algebras，central extensions and 2－Cocycle－Like indentities［J］.J Algebra，2005，288（2）：321－344.

［7］MAKHLOUF A，SILVESTROV S D.Hom－algebra structure［J］.J Gen Lie Theory Appl，2008，2（2）：51－64.

［8］HARGWIT J T，LARSSON D，SILRESTROV S D.Deformation of Lie algebras usingσ－derivations［J］.J Algebra，2006，295（2）：314－361.

［9］FAOUZI AMMAR.Cohomology of Hom－Lie superalgebras and q－deformed Witt superalgebra［J／OL］.［2012－04－27］.http：／／arxiv.org／pdf／1204.6244.pdf.

［10］王卫国.低维Leibniz超代数的分类［D］.上海：华东师范大学，2007.