数项级数的收敛性教学探讨

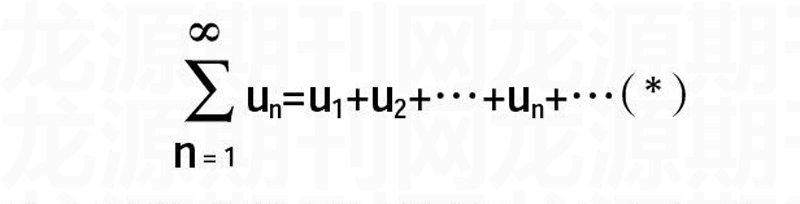
摘 要：级数的收敛性是级数理论的首要概念。对级数收敛性概念的教学进行探讨，通过问题驱动，给学生展现级数概念的形成过程。

关键词：数项级数;数学史;极限

级数是研究函数性质和进行数值计算的有力工具，在多种实际问题上的应用非常广泛。对级数的研究可追溯至对芝诺悖论的探讨，其重要性始现于微积分学的创立与发展。例如，在求解面积问题时，牛顿最初就是利用将函数表示成无穷级数的方法，进而逐项求积。另外，牛顿也使用了相同的方法来处理微分方程的问题。级数是构造非初等函数的重要方法，例如我们所熟知的积分，无法通过黎曼积分方法求出，而是通过级数的方法求解的。一旦给出了函数的级数表示，对该函数的分析性质进行探讨就很便利了。级数理论是以简驭繁的数学思想的重要体现，以物理学的观点看，这就相当于把一个复杂的运动分解为一系列简谐运动的叠加。

级数理论中的首要概念是收敛性，利用无穷级数来表示函數，即逼近问题，最终将归结为级数的收敛问题，因此，级数收敛性概念的教学是非常重要的，本文结合课堂教学实践，探讨级数收敛性概念的教学。

一、重视级数概念的形成过程，注重数学史的渗透

级数概念建立在极限基础之上，从有限和到无限和之间有了极限运算的参与，超乎学生的直观经验，抽象度高。作为级数教学的首课时，应该让学生对整章内容的框架有个大概了解，因此，扼要介绍级数的发展史是很有必要的，让学生了解数学知识是实践的产物，源于生活并服务于生活。为此，我们利用问题驱动，从芝诺悖论开始，引入级数概念。

第一环节：问题提出

Aristotle悖论（PPT演示）

问题1：无限个数相加的结果是什么？

问题2：有限个数相加的结合律、交换律对于无限和还有效吗？

第二环节：引出定义

定义1：给定一个数列un，对其各项依次用“+”号连接起来的表达式：

un=u1+u2+…+un+…（*）

称为常数项级数或数项级数（简称级数），其中称为数项级数（*）的通项或一般项。

回到我们的问题：如何判断级数（*）的结果？

先看一个例子：（让学生自由交流，与同学分享自己的结论，教师总结讨论的结果）

令S=1-1+1-1+1-1+…

结果1：S=（1-1）+（1-1）+（1-1）+…=0+0+0+…=0

结果2：S=1+（-1+1）+（-1+1）+…=1+0+0+…=1

结果3：S=1-（1-1+1-1+…）=1-S，从而S=

从上例可以看到，有限个数相加与无限个数相加是不同的，有限到无限之间经历了质的变化，有限和的交换律与结合律不能“平行移植”到无限和。在此，数学再一次发挥了其以简御繁的精神与方法，“简”即有限，“繁”即无穷，“御”即逼近：以有限项之和去逼近无穷项之和。我们可以看到，所选项数越多，近似程度越高，由此，引入“部分和”的概念：

定义2：级数un的前n项之和Sn=un=u1+u2+…+un，称为级数（*）的第n个部分和（简称部分和）。若部分和数列Sn收敛，即■Sn=S，则称级数（*）收敛，且S为其和，记作un=S。

第三环节：定义运用

例1：（解决Aristotle悖论）

解：由于Si=S+S+…+S+…，而Si=S+S+…+S==S，因此，Si=S。

这说明总路程是一段有限的距离，不可能永远也走不到终点，同时指出悖论的谬误之处。

例2：讨论S=1-1+1-1+1-1+…的敛散性。

解：S1=a1=1，

S2=a1+a2=1+（-1）=0，

S3=a1+a2+a3=1+（-1）+1=1，

S4=a1+a2+a3+a4=1+（-1）+1+（-1）=0…

Sn=1，n=2k-10，n=2k

因此，Sn不存在，级数发散。

例3：讨论等比级数arn-1=a+ar+ar2+…+arn+…（a≠0）的敛散性。

解：因为Sn=ark-1=a·，当r≥1时，显然级数发散。

当r<1时，我们有Sn=a·=。此时，级数收敛。

等比级数是非常重要的一类无穷级数，在后续学习级数敛散性判别中有重要作用。例2能让学生体会无限和与有限和的区别。

三、教学反思

极负盛名的荷兰数学教育学家Freudenthal曾说：没有一种数学思想，以它最初被发现时的那个样子发表出来。一个问题被解决以后，相应的发展成一种形式化的技巧，结果使得火热的思考变成了冰冷的美丽。本着这样的理念，教师的任务是将这些闪亮的思想过程还原给学生，引导其思考、探索，从而培养其发现问题、解决问题的能力。大学课堂是引导学生进入科学研究领域的前沿阵地之一，能把学生吸引住的，不是冰冷的定理定义，而是隐藏其后的那些火热的思考与碰撞。

参考文献：

[1]华东师范大学数学系.数学分析[M].4版.北京：高等教育出版社，2010.

[2]张奠宙，张荫南.新概念：用问题驱动的数学教学[J]，高等数学研究：2004，7（3）：8-10.

[3]Walter Rudin.Principles of mathematical analysis[M]. McGraw-Hill Companies，Inc. 1976.

作者简介：兰尧尧，女，1981.12，博士，副教授，重庆文理学院数学与财经学院，研究方向：不确定性理论及其应用

基金项目：国家自然科学基金项目（编号：11226268），重庆文理学院教学改革研究项目（编号：110235），重庆文理学院第二批特色项目（《实变函数》课程教学改革研究）。

？誗编辑 李建军