一种新型的快速信号重构算法
钱 阳,宋欢欢,李 雷
(南京邮电大学 视觉认知计算与应用研究中心,江苏 南京 210023)
一种新型的快速信号重构算法
钱 阳,宋欢欢,李 雷
(南京邮电大学 视觉认知计算与应用研究中心,江苏 南京 210023)
信号重构是压缩感知理论的关键组成部分,研究快速有效的重构算法具有现实意义。目前,迭代阈值算法中的不动点迭代(FPC)算法,在重构速度和精度方面存在很大的提升空间。为此,文中首先提出了一种快速不动点迭代(FFPC)算法。接着针对该算法,通过引入子空间优化,充分利用压缩感知贪婪算法和凸优化算法的各自优点,提出了快速不动点_活动集(FFPC_AS)算法,进而得到更加准确的解。对于FFPC_AS算法,给出了收缩阶段和子空间优化阶段交替执行方案,避免了除偏(Debiasing)操作。大量仿真对比实验表明,所提算法既能快速重构图像信号,又可以提高准确率。
压缩感知;快速不动点;活动子集;子空间优化;除偏
0 引 言
在信息数字化时代,压缩感知理论(Compressed Sensing,CS)[1-2]凭借其采样与压缩同时进行,并能精确重构出原始信号的良好性能,吸引了数学家和计算机学家的广泛关注[3]。该理论主要包括信号的稀疏表示、观测矩阵的选取和信号重构这三个阶段。其中最关键的一步是重构信号,其性能的好坏决定了重构质量的优劣与恢复时间的长短。
CS理论的目标是从较少的相对不完整的测量值b=Ax中恢复出K稀疏信号x∈Rn。目前重构算法主要集中于贪婪算法和凸优化算法。当满足等距约束条件(RestrictedIsometryProperty,RIP)[4]时,贪婪算法效果较好。这类算法主要包括正交匹配算法(OMP)[5]、子空间追踪(SP)[6]等。而典型的凸优化算法包括基于阈值的算法[7-8]、NESTA算法[9]、不动点连续方法(FixedPointContinuation,FPC)[10]等。
FPC算法是一种基于算子分裂和连续的,能够解决大规模数据密集问题的方法,被广泛应用于CS的核磁共振成像(MRI)中[11]。为了提高FPC算法的重构性能,文中通过引入软阈值和正则化参数的双收缩,提出了快速不动点迭代方法(FFPC)。该方法表现出更优的重构性能。然而,FFPC方法重构的信号存在一些误差,需要采用除偏操作去除误差较大的元素。受文献[12]中所提基于收缩的快速稀疏重构(FPC_AS)算法的启发,针对输入信号绝对稀疏时,FFPC算法重构误差较大的情况,文中通过引入子空间优化概念,建立了快速不动点-活动子集算法(FFPC_AS)。大量对比实验验证了所提算法无需除偏,而且具有最好的重构效果。
1 预备知识
1.1 压缩感知理论基础
在压缩感知理论中,如果n维稀疏信号x∈Rn在某正交基或者紧框架Ψ(其中Ψ=(φ1,φ2,…,φn)T)上可压缩,那么x在该基下可以线性表示为:
Θ=ΨTx
(1)
式中,Θ是x在Ψ变换域上的变换向量。
CS编码中,通过设计一个平稳的、与Ψ不相关的测量矩阵Φ,对稀疏信号Θ进行非自适应观测,得到观测向量b=ΦΘ=ΦΨTx(其中A=ΦΨT称为信息算子[13])。Candes等指出,为保证准确地从m个测量值中恢复出K个系数,A必须满足等距性质[14]。
实际的信号测量中,随着被测信号的不同,变换基Ψ会有相应的变化,因此希望找出可以与任意稀疏基不相关的观测阵Φ。对于任意正交基Ψ,随机产生一个测量矩阵Φ,若m≥CKlog(n/K),其中C为某固定常数,则Ψ与Φ不相关的概率就很大,即A满足RIP条件的概率很大。常用的观测阵有高斯随机矩阵、哈达玛矩阵、伯努利矩阵等。

min‖x‖0subject toAx=b
(2)

然而,l0范数模型是NP难题[15],在数值上是不可解的。因此,Candes等指出,在一定条件下,问题的解x∈Rn可以通过基追踪问题(BP)获得。

(3)
通过引入正则化参数μ,式(3)可以化为无约束最优化问题。
(4)
1.2 基于不动点方法的信号重构算法
2007年,Elaine T等首次提出解决l1范数问题的不动点算法(FPC),并将其应用于CS的信号重构中。FPC主要解决式(5)所示的l1范数问题:
(5)
其不动点迭代式为:
xk+1=Sv∘h(xk),ν=τ/μ
(6)
其中,Sv(·)是软阈值收缩算子;ν是阈值。
2010年,WenZaiwen等提出了一种基于收缩的快速稀疏重构算法—FPC_AS[16],用于求式(5)的最优解。该算法是在FPC算法的基础上,引入子空间优化,集成了阈值迭代算法求解速度快和凸优化算法易获得全局解的优势,从而得到式(5)更加精确的解。尽管如此,FPC算法在重构速度和精度方面仍存在很大的提升空间。
2 快速不动点迭代算法(FFPC)
传统FPC方法的收敛速度由ν=τ/μ和二次函数f(x)的部分Hessian矩阵HEE的谱性质决定,在特定的参数τ下,不动点方法是线性收敛的。为提高FPC算法的收敛速度和信号重构质量,引入软阈值步长参数和正则化参数的收缩,提出了快速不动点迭代算法。
FFPC算法求解的是问题(5)中M=2的情况,其中μ是引入的正则化参数,用来平衡l1,l2范数所占的比重,利用优化算法可求得最优解x*。
(7)

(8)

使用式(8)更新x类似于使用最速下降方法,在满足式(9)的基础上,使用式(10)来寻找最优步长tk。
(10)
因此,更新不动点迭代式(6)为:
式中,⊙是按元素逐个作乘积的算子;ν=τ/μ为阈值,对确定不动点迭代式(11)的收敛速率起重要作用,ν值越大,收敛速率越快。因此只要使τ的值尽量大,μ的值尽量小,就能加快不动点迭代(11)的收敛速度。
利用BB(Barzilai和Borwein)步长更新参数τ。
(12)
对于参数μ,其作用是来平衡二次项f(x)和l1范数项‖x‖1的比重,通常设置δ·max(ATb)(δ是大于0的常数)作为参数μ的初始值。此外,在迭代过程中,为加快x的稀疏速度,可以对μ作适当的收缩操作,即令μ=β·μ(其中β是收缩因子,0<β<1),并且保证μ仍然能够平衡二次函数f(x)和l1范数‖x‖1在迭代过程中的比重。
在FFPC算法中,两次相邻迭代的相对误差决定了其迭代终止条件:
这里,迭代终止条件为xtol和gtol。当满足上述条件时,FFPC算法停止迭代。
利用FFPC算法恢复信号x,具体执行步骤如下:
Step1:令信号在小波域的稀疏表示为x0=0,设置迭代次数初始值k=1,t1=1,z1=0。
Step2:利用式(6)计算xk。
Step3:计算tk+1,根据式(9)对t进行更新,利用式(8)计算zk。
Step4:按式(13)计算函数Gk(xk,xk-1),若满足终止条件,则令x*=xk,否则转Step5。
Step5:扩张参数μ=β·μ,令k=k+1,更新τ,将zk代入Step2中,重复上述过程。
迭代结束后,得到的迭代结果x*即是对原始信号的估计值。
3 快速不动点_活动子集(FFPC_AS)
尽管FFPC算法比FPC算法表现出更优的重构性能,但和FPC算法一样,重构出的信号存在一些误差,需要采用除偏操作去除误差比较大的元素。针对在输入信号绝对稀疏时,FFPC算法重构结果误差较大的情况,受文献[16]的启发,文中提出了快速不动点-活动集算法(FFPC_AS)。该方法在利用FFPC重构信号后,通过提取重构结果非零项的索引,建立活动子集,并进行子空间优化操作,在确保信号重构准确度的基础上,提高算法收敛速度。
FFPC_AS算法分为收缩阶段和子空间优化阶段。收缩阶段利用FFPC算法逼近原始信号x,得到粗糙解xk,并且计算活动集A(xk);当活动集A(xk)逼近于真实的活动集A(x*)时,利用二阶方法求解子空间优化问题即可。不断地重复这两个阶段,直至满足精确解条件。
3.1 收缩阶段
令dk=d(τk)(xk)为线性搜索的搜索方向,则dk可以按照下面方法进行计算。
dk(x)=xk-xk-1,k>1
(14)
其中,xk是FFPC算法第k步迭代得到的结果,令x+=xk+αkdk,则不动点迭代式为:
xk=S(x+-τg,τ/μ),μ>0,τ>0
(15)
(16)
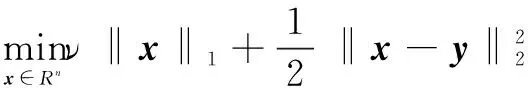
(S(x,ν)-x)T(y-S(x,ν))+ν(ξ-
‖S(x,ν)‖1)≥0
(17)
用x-τg和‖x‖1,分别替换y和ξ,并且令ν=τ/μ,则式(17)可写为:
(S(x-τg,τ/μ)-(x-τg))T(x-S(x-τg,τ/μ))+τ/μ(‖x‖1-‖S(x-τg,τ/μ)‖1)≥0
代入式(14)、(15)得:
(18)
minμf(x)+ξs.t. (x,ξ)∈Ω
(19)
因为ξ*=‖x*‖1,故其对于不动点x*的一阶最优性条件为:
μf(x*)(x-x*)+(ξ-‖x*‖1)≥0 ∀(x,ξ)∈Ω
(20)
因此,用dk求解问题(5)类似于求解式(19)的梯度投影方法,当且仅当x*是式(15)的驻点时,对∀x*∈Rn,0<τ<∞,有:
d(τ)=0
(21)

ψ(xk+αkdk)≤Ck+ρhσΔk
(22)


(23)
由于式(18)和l1范数的凸性,故存在(回溯)步长满足式(22)的要求,其中Ck=Φ(xk)。该线性回溯方法是单调的,因为Φ(xk+1)<Φ(xk)。
FFPC_AS算法中使用了一种快速的非单调的线性搜索方法—FNMLS。
Ck+1=(ηQkCk+ψμ(xk+1))/Qk+1
(24)
其中,Ck是函数ψμ(xk)和Ck-1的凸组合;Qk+1=ηQk+1,Q0=1,0<η<1。
算法过程如下:
初始化:x0,设置参数0<η<1,t0=1和0<τm<τM<∞。
令C0=Φ(x0),Q0=1,k=0。
WHILE“不满足收敛条件”DO
计算搜索方向:令τm<τk<τM,令dk=S(x+-τkgk,τk/μ)-xk-1。
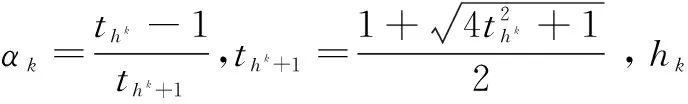
更新:令Qk+1=ηQk+1,Ck+1=(ηQkCk+
Φ(xk+1))/Qk+1,k=k+1。
ENDWHILE
在迭代过程中,Ck的值随着迭代次数的增加而变大。
3.2 子空间优化阶段
对于固定的常数δ,满足下面任意一个条件,即可由收缩阶段转换到子空间优化阶段。
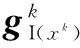


(25)
(26)

(27)

至此,子空间优化为可简化为:
minφμ(x) s.t.x∈Ω(xk)
(29)
该子空间优化问题可以由共轭梯度方法来求解。
FFPC_AS算法:

(2)重复迭代直至收敛。
●阈值收缩阶段。

令tk=1。若ψμk(xk+)>Ck+σαkΔk,那么用FNMLS算法搜索αk。更新x+=xk+αkdk,Qk+1=ηQk+1,Ck+1=(ηQkCk+Φ(xk+1))/Qk+1。
计算非活动集I(xk+1,ξk)和活动集A(xk+1,ξk),更新阈值ξk+1=min(max(η2
若χ(xk+1,μ,ξk)≤max(ε,εxmax(‖xk+1‖,1)),则收缩阶段结束。
●检查是否需要做子空间优化。
令do_sub=0,若I(xk,ξk-1)≠I(xk+1,ξk),则

设置do_sub=1,δ=γδ。否则若
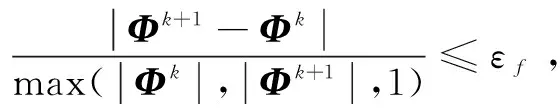
●做子空间优化。
若do_sub=1,那么

若χ(xk+1,μ,ξk)≤max(ε,εxmax(‖xk+1‖,1)),则返回结果集。
若χ(xk+1,μ,ξk)≤max(ε,εxmax(‖xk+1‖,1))或者do_sub=1,并且μk>μ,那么
计算μk+1=max(βmin(‖gA(xk+1,ξk)‖,μk),μ)。令δ=δ0,Ck+1=Φ(xk+1),Qk+1=1。
否则令μk+1=μk。
4 仿真实验及实验结果分析
以256*256的自然图像Camera进行实验仿真。实验平台为Windows8.1,Intel(R)Core(TM)2DuoCPU,2.53GHz,实验设计基于Matlab7.11.0编程实现。采用DCT稀疏变换基,观测矩阵选用高斯随机矩阵。初始正则化参数μ=10-10。迭代过程中,设置收缩因子β=0.1,非线性搜索参数γ=0.85,σ=0.5,δ=10-6,执行子空间优化条件参数εf=10-20。

图1 算法性能随采样率变化图
图1记录了随着采样率变化不同算法对Camera图像重构性能的变化曲线。
实验中,由于FPC_AS、FFPC_AS算法均采用一阶收缩方法和二阶共轭梯度(CG)方法交替求解的方式来逼近最优解,而其他算法则是一阶算法,故FPC_AS与FFPC_AS算法的收敛速度要快些。图(a)形象地展现了FPC_AS和FFPC_AS的重构速度。当采样率超过0.6时,二阶子空间优化次数较多,算法收敛至精确解的速度更快。图(b)展示了在不同采样率下,FFPC_AS算法重构出的图像的峰值信噪比都是最高的。
表1给出了不同采样率下对FPC和FFPC算法所得结果进行除偏操作的重构情况。
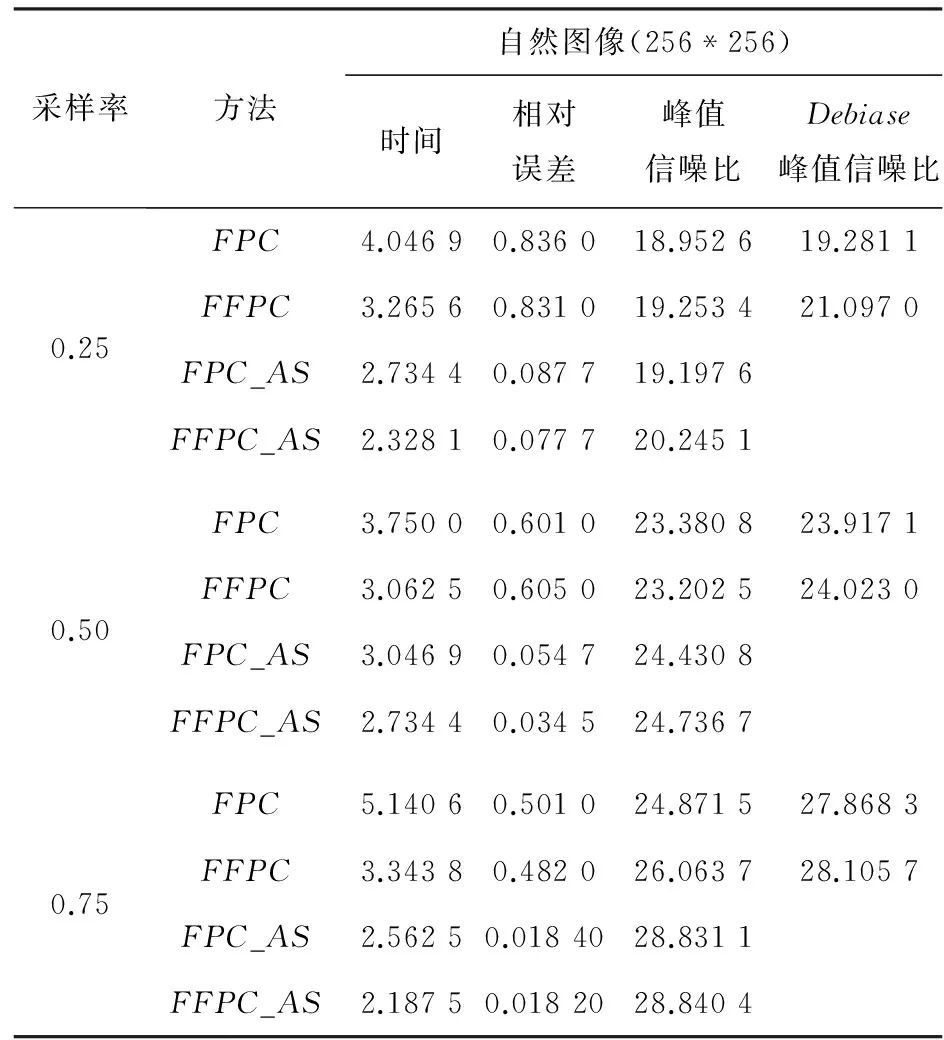
表1 Camera图像处理结果
由表1可见,FFPC_AS算法重构速度最快,在采样率为0.5和0.75时,FFPC_AS的峰值信噪比要比FFPC经过除偏(Debiase)的值要高出0.713 7dB和0.734 7dB。
为验证文中算法重构性能最优,分别采用FPC_AS和FFPC_AS算法对Camera图像进行重构。图2和图3分别给出了不同采样率下两种算法的重构效果直观图。

图2 自然图像Camera的FPC_AS处理结果

图3 自然图像Camera的FFPC_AS处理结果
从图中不难发现,FFPC_AS的重构效果更好些。在采样率为0.25和0.5时,结果图中均存在些噪点,FFPC_AS的重构图细节更加明显。而当采样率达到0.75时,两种方法的重构图像细节突出,对比度很高。
5 结束语
文中首先对传统的不动点迭代方法(FPC)进行改进,通过引入软阈值步长参数和正则化参数的收缩,形成快速不动点迭代(FFPC)算法;接着针对FFPC算法需要进行除偏操作的缺陷,提出了快速不动点-活动子集(FFPC_AS)方法。该算法结合了一阶FFPC方法和二阶共轭梯度方法的优势,在FFPC算法求得结果的活动子集逼近精确解的活动子集时,利用二阶共轭梯度方法再来逼近精确解,不仅能使FFPC_AS算法更快速地收敛至最优解,而且大大提高了解的准确度。仿真实验结果表明,文中所提算法在图像重构的质量和速度方面有明显优势。
[1]CandesE,RombergJ.Quantitativerobustuncertaintyprinciplesandoptimallysparsedecompositions[J].FoundationsofComputationalMathematics,2006,6(2):227-254.
[2]DonohoDL,TsaigY.Extensionsofcompressedsensing[J].SignalProcessing,2006,86(3):533-548.
[3]KashinBS,TemlyakovVN.Aremarkoncompressedsensing[J].MatematicheskieZametki,2007,82(6):829-837.
[4]CandesE,TaoT.Nearoptimalsignalrecoveryfromrandomprojections:universalencodingstrategies[J].IEEETransactionsonInformationTheory,2004,52(12):5406-5425.
[5]MallatS,ZhangZ.Matchingpursuitswithtime-frequencydictionaries[J].IEEETransactionsonSignalProcessing,1993,41(12):3397-3415.
[6]DaiW,OlgicaM.Subspacepursuitforcompressivesensing:closingthegapbetweenperformanceandcomplexity[R].Urbana,IL:UniversityofIllinoisatUrbana-Champaign,2008.
[7]CombettesPL,PesquetJC.Proximalthresholdingalgorithmforminimizationoverorthonormalbases[J].SIAMJournalonOptimzation,2007,18(4):1351-1376.
[8]BeckA,TeboulleM.Afastiterativeshrinkage-thresholdingalgorithmforlinearinverseproblems[J].SIAMJournalonImagingScience,2009,2(1):183-202.
[9]BeckerS,BobinJ,CandesE.NESTA:afastandaccuratefirst-ordermethodforsparserecovery[R].Pasadena:CaliforniaInstituteofTechnology,2009.
[10]HaleET,YinW,ZhangY.Fixed-pointcontinuationforl1-minimization:methodologyandconvergence[J].SIAMJ.Optim.,2008,19(3):1107-1130.
[11] 刘晓曼,丛 佳,朱永贵.不动点方法及其在压缩感知核磁共振成像中的应用[J].中国传媒大学学报:自然科学版,2014,21(1):28-34.
[12]HaleET,YinWotao,ZhangYin.Afastalgorithmforsparsereconstructionbasedonshrinkage[J].SIAMJournalonScientificComputing,2010,32(4):1832-1857.
[13]BaraniukR.Alectureoncompressivesensing[J].IEEESignalProcessingMagazine,2007,24(4):118-121.
[14]CandesE,RombergJ,TaoTerence.Robustuncertaintyprinciples:exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETransactionsonInformationTheory,2006,52(2):489-509.
[15] 焦李成,公茂果,王 爽,等.自然计算、机器学习与图像理解前沿[M].西安:西安电子科技大学出版社,2008.
[16]WenZ,YinW,GoldfarbD,etal.Ontheconvergenceofanactivesetmethodforl1minimization[R].NewYork:ColumbiaUniversity,2008.
A Novel Fast Signal Reconstruction Algorithm
QIAN Yang,SONG Huan-huan,LI Lei
(Center for Visual Cognitive Computation and Its Application,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)
Signal recovery is the key component of compressed sensing theory,which has practical significance to research the fast effective reconstruction algorithms.At present,the convergence rate and accuracy of Fixed Point Continuation (FPC) algorithm still can be improved.So,a Fast Fixed-Point Continuation (FFPC) algorithm is put forward firstly,and then it makes full use of the respective advantages of greedy algorithm and convex optimization by introducing subspace optimization to come up with the fast Fixed-Point Continuation_Active Set (FFPC_AS) algorithm,which can improve the accuracy and the convergence rate of FFPC algorithm.For the FFPC_AS algorithm,the shrinkage phase and subspace optimization phase are performed repeatedly which can avoid the debiasing operation,and the embodiment of the two stages is given in this paper.A large number of comparative simulation results show that the proposed algorithm exhibits state-of-the-art performance in terms of both its speed and its ability to recover sparse signal.
compressed sensing;fast fixed-point continuation;active set;subspace optimization;debiasing
2015-09-21
2015-12-23
时间:2016-05-25
国家自然科学基金资助项目(61070234,61071167,61373137,61501251);南京邮电大学引进人才科研启动基金资助项目(NY214191);江苏省2015年度普通高校研究生科研创新计划项目(KYZZ15_0235)
钱 阳(1991-),女,硕士生,研究方向为非线性分析及应用;李 雷,博士,教授,研究方向为智能信号处理和非线性科学及其在通信中的应用研究。
http://www.cnki.net/kcms/detail/61.1450.TP.20160525.1709.058.html
TP301.6
A
1673-629X(2016)06-0056-06
10.3969/j.issn.1673-629X.2016.06.012

