解题以后还可以做些什么？

吴文尧

浙江省宁波市北仑中学　(315800)



解题以后还可以做些什么？

吴文尧

浙江省宁波市北仑中学(315800)

圆锥曲线解答题是高考数学的必考内容，有许多同学抱怨，虽然做了大量的圆锥曲线练习题，但解题水平提高不是很明显,在应试中对圆锥曲线解答题还是心有余悸．出现这种现象的其中一个很重要原因是：在解题训练中，为解题而解题,缺少了一个很重要的环节——解题以后的总结和反思.本文以一道圆锥曲线试题为例,谈一谈解题以后还可以做些什么,从而达到通过少量的训练提高解题水平的目的.

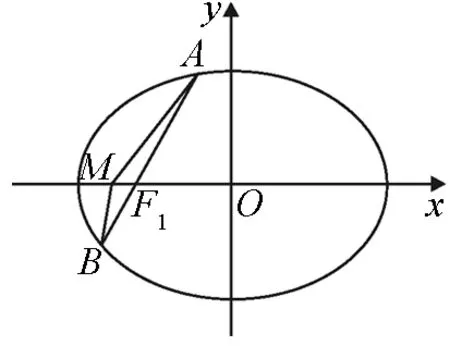
图1

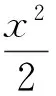
一、看一看——结论是否正确，过程是否合理和完整

“会而不对,对而不全”是高中数学考试中最容易出现的问题,每做完一道试题,看一看结论是否正确,过程是否合理和完整,是防止这种情况发生的最有效的手段.不难发现,本题是一道比较常规有关圆锥曲线的定值问题,相信多数同学能解决这个问题.下面给出的证明方法之一可能是最容易想到的方法,不妨请大家先看一看,其解题过程是否存在不足之处．

分析:由于直线l是过点M的任意直线,直线l的斜率有可能不存在,所以上述解题过程忽视了斜率不存在的情况.故本题需对直线l的斜率是否存在进行分类讨论.其完整解答如下:

(2)当直线l的斜率存在时，设直线l的斜率为k(以下同解法一).

评注：在运用直线方程解题时，忽视直线方程的适用范围是同学们最容易犯的错误之一；对于本题若先考虑直线l的斜率不存在时的情况，不但可使解题过程显得完整，还可从中猜想其定值的大小，在解题中起“导航”的作用．

二、理一理——解决这类问题的思想方法及解题规律

平时解题训练的目的是提高解决问题的能力，而解题后的反思和总结是收获解题经验、提高能力的重要环节，因此解完一道题后理一理解决这类问题的思想方法是什么？是否有一般的解题规律？应该成为我们自觉的行动，这样才能做到举一反三，提高复习的效果．

由于本题是一个圆锥曲线中的定值问题，而定值问题的本质是与之相关的函数恰是一个常数函数，所以可运用函数的观点分析解决问题，即应以函数的思想为解题的指导思想．

解决定值问题的解题程序为可归纳为：一选，二求，三定值.

一选:选择参变量.需要证明为定值的量在通常情况下“照理”应该是个变量,它应该随某一个量的变化而变化,可选择这个量为参变量(有时可选择两个参变量,然后由其它辅助条件消去其中之一).

二求:求出函数的解析式.即把需要证明为定值的量表示成关于上述参变量的函数.

三定值:化简函数解析式得到定值.由题目的结论可知要证明为定值的量必与参变量的大小无关,故求出的函数必为常数函数,所以只须对上述函数的解析式进行必要的化简即可得到定值.

三、试一试——解决本题是否还有更好的方法

运算复杂是圆锥曲线问题成为难点的一个重要原因，要突破这个难点一般可通过以下两个途径，其一是努力提高自己的运算能力，特别是有关字母运算的能力；其二是注意解题方法的选择，努力简化运算过程．所以在平时的训练中要重视一题多解，注意各种方法的对比，只有这样才能在应试中能选择最合理、最简捷的解法．

对于本题，运算过程的繁简程度取决于目标函数的自变量的选择．前面给出的证法一是以直线l的斜率为目标函数的变量；注意到直线l过x轴上的一个点F1(-1,0)，所以可设直线l的方程为x=ty-1,(其中t为斜率的倒数)，即可选择t为目标函数的变量．

证法二(以直线斜率的倒数为目标函数变量):

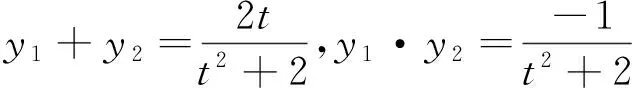
评注：证法二与方法一本质上相同，只是在直线方程形式的选择上作了一点改变，其运算过程显得比方法一要简捷一些；合理选择直线方程也是简化解析几何运算过程的重要途径之一．

注意到动直线l经过x轴上的定点F1是椭圆的焦点，因此也可考虑利用椭圆的焦半径公式(角度形式)解之，所以也可选择直线l的倾斜角为目标函数的变量．

证法三(以直线AB的倾斜角为目标函数变量)：设直线AB的倾斜角为θ,不妨设|AF|≥|BF|.

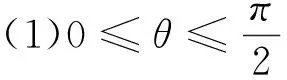
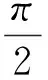
评注：本证法之所以比前面的两证法要简捷，是因为借助了椭圆的焦半径公式，充分利用其几何意义解决问题．关于圆锥曲线的焦半径公式详见文[1]．

证法一、二，其运算过程比较复杂的原因是无法回避“把直线方程代入椭圆方程并整理得……”这样的过程．若注意到AB是椭圆的一条弦，因此也可以点A,B对应的参数为目标函数的变量，再利用“直线AB过椭圆的左焦点”把双变量问题化归为单变量问题．即以椭圆的参数方程中的参数为目标函数的变量．

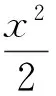
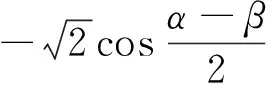
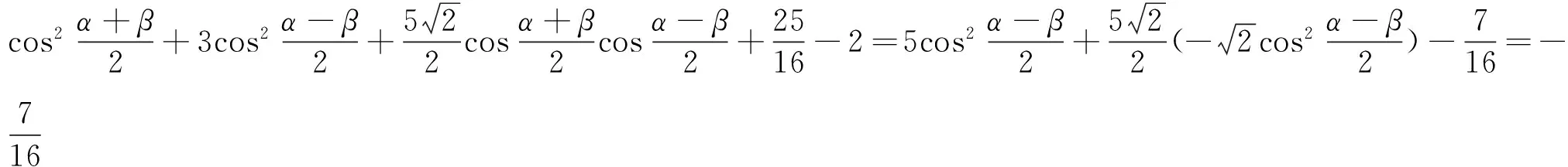
评注：本解法的基本思路是把原问题化归为一有关三角函数的定值问题；所以必须有很好的三角变换的功底才能驾驭这种证法．

四、想一想——原问题的逆命题是否正确？如何证明之

原命题与其逆命题虽然不一定同是真命题，但当它们同是真命题时，解决它们的思想方法必有许多相似之处，因此在做完一个题后，习惯性的想一想其逆命题是否成立，不但能加深对原问题的理解和掌握，而且还能在复习应试中收到事半功倍的效果．本题的逆命题即是一个逆向的定值问题，下面讨论它的正确性．

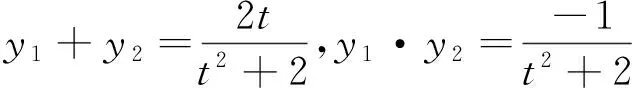
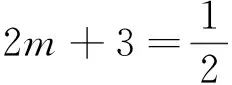
五、探一探——原问题是否可以推广到一般情况

原问题给出的是一个特殊的椭圆，对于这个椭圆具有这样的性质，我们很自然的联想到对于一般的椭圆是否也具有这种漂亮的性质？即原问题是否可以推广到一般的情况？

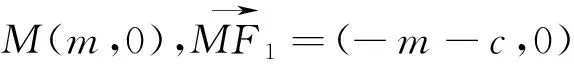
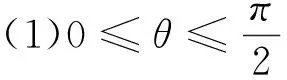
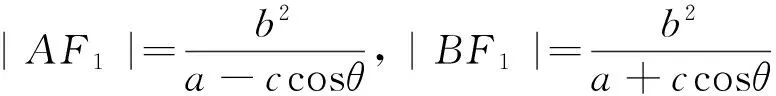
[1]吴文尧.介绍一组优美的圆锥曲线焦半径公式[J]．数学通讯.2012,3．