横看成岭侧成峰，透过现象看本质
——谈问题切入点选择

陈国春

江苏省滨海中学　(224500)



横看成岭侧成峰，透过现象看本质
——谈问题切入点选择

陈国春

江苏省滨海中学(224500)

在平时的学习和考试中，在所难免会遇到一些有难度的题目.很多学生都会提出一个问题：遇到一些比较陌生的题目时，不知道解决问题的突破口和切入点在什么地方，头脑一片空白；或者可能会有一些想法，但因为切入点选择的不合理，导致解题繁琐，从而失去解题的信心.本文笔者通过分析一道经典的调研试题的切入点去说明遇到一个数学问题时，我们如何去分析问题，如何去寻找解决问题的突破口和切入点.

一、题目再现

在ΔABC中，G为ΔABC的重心，且AG⊥BG,则sinC的最大值为．

这是盐城市高三的一道调研试题.考试过后，笔者所任教班级里的学生普遍反映：题目比较陌生，信息量很少，不知道切入点在哪，很茫然.可事实是否真的如学生所说呢？下面笔者给出解决此问题的几个切入点，供大家参考指正.

首先题目中有一个垂直的条件比较熟悉，而我们对于垂直这一条件又有哪些常见的处理方法呢？

二、横看成岭(切入点一)

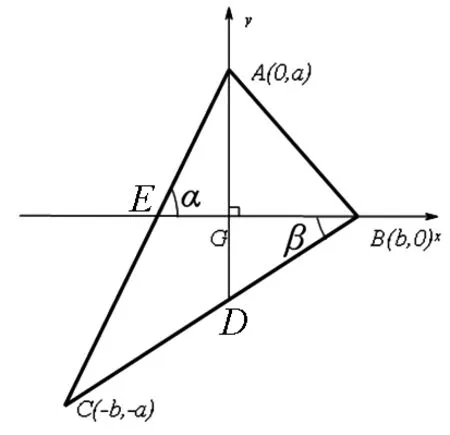
图1

根据垂直的条件AG⊥BG.根据AG⊥BG这一条件，我们很容易想到建系，将几何问题代数化去解决.建立如图1所示的平面直角坐标系.设A(0,a)，B(b,0)，因为G为重心，易得C点坐标为(-b,-a).

在建系的前提下，我们又可以尝试以下两种方法：

方法1：利用余弦定理和基本不等式可知

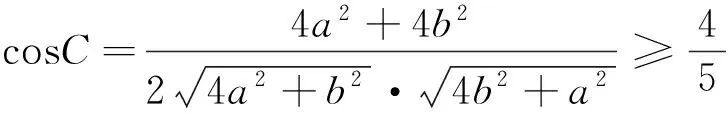
点评：这两种方法本质上都是建系寻找到点的坐标之间的关系(本质上是三边之间的关系)，然后利用余弦定理和基本不等式解决问题.

事实上我们还可以通过以下两种方法去寻找到三边之间的关系.

方法3：在直角ΔAGB、ΔAGE、ΔBGD、ΔDGE中，分别利用勾股定理易得BC2+AC2=5AB2,再用余弦定理和基本不等式易得结果.

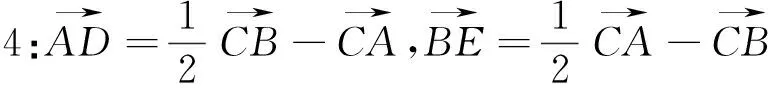
从上面这些方法我们可以发现，抓住垂直这一条件，结合平时处理垂直的常用手法，可以从多个方向进行突破.

题目中还有另外一个条件：G为ΔABC的重心，我们能不能从这一条件入手解决问题呢？笔者经过思考整理形成如下的解法：

三、侧看成峰(切入点二)

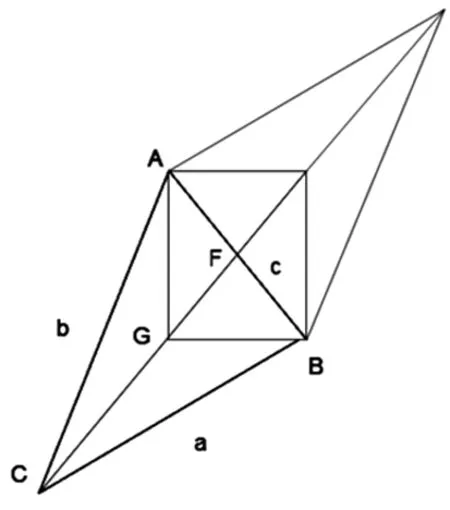
图2

G为ΔABC的重心.

所以2(a2+b2)=c2+(3c)2=10c2，再用余弦定理和基本不等式即可得到.

有句话说得好：没有无缘无故的爱，也没有无缘无故的恨.题目中给出的条件也一样.G为ΔABC的重心和AG⊥BG这两个条件也不应该是孤立的条件.

四、透过现象、寻求本质(切入点三)

G为ΔABC的重心和AG⊥BG合二为一.

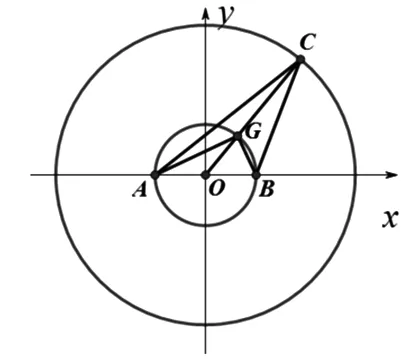
图3

我们知道对于重心还有一个比较重要的几何性质：OG∶GC=1∶2.

将AG⊥BG这一条件和圆中的知识联系起来就有了如下的几何方法：

如图3所示：不妨设小圆和大圆的半径分别为1和2，点C为大圆上一点，连接OC交小圆于点G,则ΔABC即为满足题意的三角形.题目即转化为点C在圆上运动时，要使角C最大，由著名的米勒定理可知：当过点A，B的圆与点C的轨迹即大圆相切时，角C最大.

图4

点评：横看成岭侧成峰，透过现象看本质，形成探究意识，培养探究能力.

五、反思总结

通过上面这些解决问题的切入点和方法的选择，我们发现在平时的教学中应该鼓励学生多从条件入手，结合常见的处理方法认真分析条件，努力寻找问题的突破口.我们教者更应该反思：为什么学生在处理问题时没有能够合理的从上面这些切入点去解决问题，这与我们平时的教学渗透肯定是分不开的.因此我们在平时的教学过程中应该注重数学综合素养的培养，注重学生分析问题解决问题能力的提高，不能单纯的就题论题.

笔者结合自己平时教学之后的反思给出下面两道题供读者参考，并共同思考在平时的教学过程中如何去培养学生分析问题、解决问题的综合数学素养.

题目1(2016苏北四市一调研11题)已知

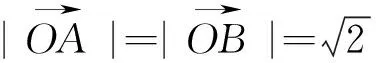
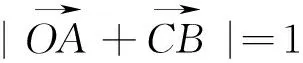
(建议：从建系，取模平方，向量加法的几何意义，三角不等式的向量形式，函数与方程等切入点分别考虑都可以解决此题)

图5

k1=λk2，求λ的取值范围.