一种PID参数闭环整定的新方法研究

王建龙， 袁德成， 王功明

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

一种PID参数闭环整定的新方法研究

王建龙， 袁德成， 王功明

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

对于被控对象模型未知的控制系统，利用闭环阶跃响应所得数据进行PID控制器的参数调节，此方法仅需用PD控制器对被控对象进行一次闭环阶跃响应即可根据关系式得出PID控制器的比例系数、积分时间常数，以及微分时间常数.从闭环阶跃响应中获取超调量与峰值时间两个性能指标，以及控制器增益、控制器微分时间常数，经过一系列模型为二阶时滞加纯滞后的被控对象试验测试可得：所求PID控制器参数中的比例系数、积分时间以及微分时间分别与响应中的控制器增益、控制器微分时间常数、超调量，以及峰值时间成一定的函数关系.新整定方法与SIMC法(令τc=θ)相比，不仅使得到的系统鲁棒性更高，而且在控制系统的响应性能上也更优越.

PID控制器； 闭环响应； SIMC； 二阶时滞加纯滞后模型

经典的PID控制器参数整定方法大多是建立在开环过程模型的基础上，以IMC(内模控制法)[1]等一系列直接合成类[2]整定方法为例，其优点在于对设定值变化响应能获得良好的响应性能；但对时间延迟常数较大的滞后过程(包括积分过程)负载扰动响应的控制效果欠佳.经典的开环整定方法还有Skogestad提出的SIMC法[3]，通过降低积分时间参数来增加积分控制对大延迟被控系统的作用强度，以提高对负载扰动的抑制作用.虽然此类开环整定方法在工业生产中获得了较广的应用，但在获得被控对象的开环过程模型过程中存在一定的弊端，例如在利用开环试验获取过程模型的数据参数时，耗时较大且对被控对象造成扰动甚至使对象失控，而且在某些情况下不容许进行开环测试，用闭环测试会更有效.最早的PID参数整定方法——Z-N法[4]也用闭环响应法，即用纯比例控制作用使被控系统达到等幅振荡状态，获得临界增益和振荡频率值，然后按经验公式计算PID控制器的3个参数.但Z-N法的一个缺点是需要系统出现临界振荡即达到不稳定的边缘；另一个缺点是低于二阶的过程用纯比例控制，可能观察不到等幅振荡现象，而且测试得到的两个参数(临界增益和振荡频率值)用于计算PID的3个参数也不方便.

本文研究了一种新的PID控制闭环参数整定方法，对PD控制器与被控对象组成的闭环系统进行设定值阶跃响应，利用响应所得数据进行控制器参数整定.新方法操作简便，让受控对象在闭环条件下得到控制只需进行较少的试验次数即可，在进行整定试验时无需让受控系统到达不稳定的边缘.

1 SIMC与夏姆斯设定值法

1.1 SIMC整定法

二阶时滞加纯滞后模型(STPD):

(1)

式中，k为过程增益；T1为主时间常数；θ为等效的纯滞后时间；T2为次时间常数(数值较T1小，但T2>θ).对于被控对象为二阶模型的PID控制器，SIMC的整定公式[3]为：

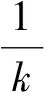
(2)

Ti=min{T1,4(Tc+θ)}

(3)

Td=T2

(4)

基于快速和平稳的控制要求，令可调参数τc等于期望闭环响应时间θ，让控制系统的响应性能和鲁棒性达到一个平衡状态.

SIMC调节方法的第一步需要把受控对象的模型降价到一阶时滞加纯滞后模型(FTPD)或二阶时滞加纯滞后模型(STPD)，第二步再利用得到的模型参数进行PID参数整定.第一步的模型降阶所用方法有：(1) 开环阶跃响应测试法；(2) 闭环阶跃响应测试法[5]；(3) 利用辨识方法得到系统的精确模型后再用减半原则降阶.虽然法(2)可以利用闭环响应测试法得到受控对象模型，但此方法仍需进行两步操作，另外在获取过程模型时可能会用到近似法，使得到的模型数据有所失真.

1.2 夏姆斯设定值法

为减少整定过程所需步骤，Shamsuzzoha[6]提出在纯比例控制下利用设定值阶跃变化的闭环响应数据直接进行PI控制器的参数整定，此法是在SIMC方法的基础上，对一系列一阶时滞加纯滞后对象进行实验得出的.它可以在被控对象模型未知的情况下，利用闭环响应所得数据进行PI控制器的参数整定.

现在用二阶对象模型替代一阶对象模型，用PD控制器替代P控制器，取一系列从时滞过程到延迟(积分)过程的二阶被控模型，并对响应所得数据进行拟合分析.PD控制器有增进调节系统稳定度的优点，并可调小比例度，从而加快调节过程，减少动态偏差和静差.比例微分控制器相比较于纯比例控制器虽然微分作用不直接影响系统的稳态误差，但它增加了系统的阻尼，因此可以允许采用比较大的增益K值，这将间接地改善系统的稳态精度[7].对于有较大惯性或滞后的被控对象，比例微分(PD)控制器能改善系统在调节过程中的动态特性.

2 参数整定式的获得

2.1 闭环实验

利用被控对象为二阶时滞加纯滞后的系统进行闭环实验，并根据所得实验数据进行PID控制器参数整定，闭环实验选取设定值阶跃响应.

实验步骤如下：

(1)在PD控制器下做设定值阶跃变化的闭环响应，保持受控系统处于稳定状，如图1所示.

图1 PD控制下闭环阶跃设定响应

(2) 记录以下实验数据：Kc0为实验中出现振荡时对应的控制器增益；Td0为实验中出现振荡时对应的控制器微分时间常数；tp为设定值阶跃变化后闭环响应出现的第一个峰值的时间；Δys为设定值阶跃变化的大小；Δyp为设定值阶跃变化后闭环响应出现第一个峰值时对应的输出变化值；Δy∞为设定值阶跃变化后闭环响应最终的稳态值；y0为响应的初始值.并计算超调量：

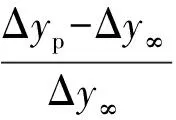
(5)

Δy∞的值需要响应稳定之后才能获得，但当超调量的取值相对较大时，响应需要经过较长的时间才能达到稳态，在此种情况下，可以在响应达到第一个负峰值时终止响应并记录此时的峰值Δyu，并由以下公式计算Δy∞的值：

Δy∞=0.45(Δyp+Δyu)+0.1y0

(6)

(3) 不断调整比例系数和微分时间常数，得到所需的不同超调量和峰值时间的闭环实验数据.

通常，可以利用设定值阶跃变化的闭环响应实验数据来得到受控对象的模型参数值[7]，然后再用SIMC整定方法的第二步得到控制器参数.下面所推导的是利用实验数据直接计算控制器参数的新整定方法，得到一个阶跃响应数据和SIMC整定公式(2)、(3)、(4)之间的关系式，即参数整定式.

2.2Kc的整定式

2.2.1 获取响应试验数据

(1) 首先固定PD控制器的微分时间常数Td0，通过调整控制器的比例参数值Kc0让闭环响应产生确定的超调量值，即得到超调量分别为0.1、0.2、0.3、0.4、0.5、0.6的6组闭环响应试验数据.

(2) 改变PD控制器Td0的大小，并再次调整比例参数值，得到6组确定超调量大小的闭环响应试验数据.

(3) 对于每一个模型共改变5次Td0的取值，即分别令Td0=0.10、0.25、0.35、0.50、0.60，因此，共得到6×5组设定值阶跃闭环响应数据.

为了使15个模型的响应试验都能获得0.1～0.6的超调量，在这30组试验中，Td0的取值范围为0.1～0.6，因此从因子分析(factor analysis)的角度，Td0的取值需要包含最小值、最大值以及中间值，分别为0.10、0.35、0.60.

记录15个模型共6×5×15组响应中比例增益Kc0的取值.

2.2.2 数据拟合分析

对实验数据进行分析后发现，对于确定的超调量σ与微分时间常数Td0，Kc与Kc0成线性比例关系：

(7)

而且比值A的大小取决于σ与Td0，与模型参数量T1/θ的取值无关.以Td0=0.1为例，在不同超调量σ下，对相应的实验数据进行分析，结果如图2所示.

图2 不同超调量下Kc与Kc0的数据拟合(Td0=0.1)

当阶跃响应的超调量确定，而微分时间常数Td0改变时，A的数值也相应改变.对相应数据进行拟合分析，以超调量σ=0.3和σ=0.4为例，拟合分析结果如图3、图4所示.

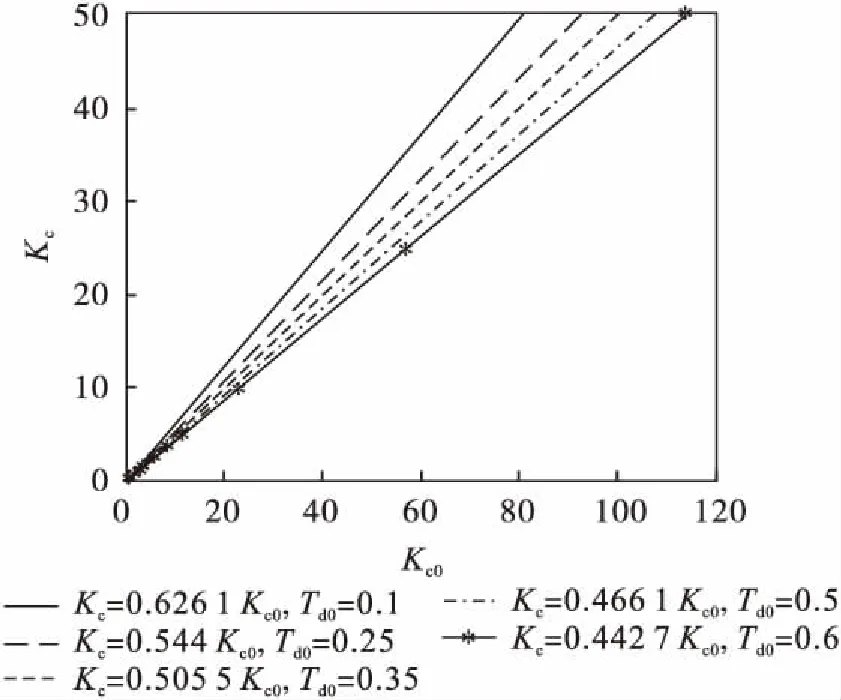
图3 σ为0.3时Td0对A的影响

图4 σ为0.4时Td0对A的影响

综上所述，比值A是由微分时间常数和超调量共同决定的.通过数据拟合后得到比值A与微分时间常数Td0成以下函数关系：

(8)

数据拟合如图5所示.其中a、b、c的取值与超调量σ成以下函数关系：

a=2.933σ2-2.975σ+1.062

b=-3.59σ2+3.811σ-1.502

(9)

c=1.47σ2-1.592σ+1.144

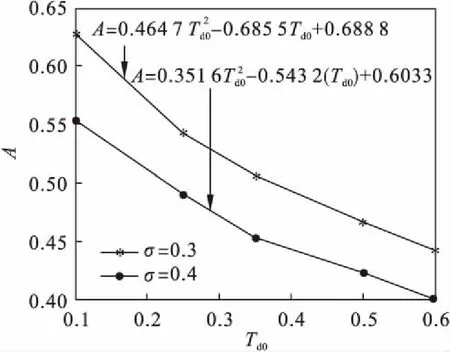
图5 比值A与Td0的拟合关系

数据拟合如图6所示.

综上所述，Kc的整定式如(7)、(8)、(9)式所示.

图6 系数a、b、c与σ的拟合关系

2.3Td的整定式

(1) 首先设定控制器的比例参数值Kc0为确定值，通过调整控制器的微分时间参数值Td0让每组闭环响应产生确定的峰值时间，即得到tp分别为2.5、2.6、2.7、2.8、2.9、3.0的6组闭环响应试验.

(2) 改变PD控制器Kc0的大小，并再次调整微分时间常数参数值Td0，得到6组确定峰值时间的闭环响应试验.

(3)对于每一个模型共改变3次Kc0的取值，令Kc0分别为1.00、1.25、1.50，总共得到6×3组设定值阶跃变化闭环响应.为了使11个模型的响应试验都能获得数值为2.5～3.0的峰值时间，在这18组试验中Kc0的取值范围为1.00～1.50，因此，从因子分析(factor analysis)的角度，Kc0的取值需要包含最小值、最大值以及中间值，分别为1.00、1.25、1.50.

记录11个模型共11×6×3组响应中微分时间常数Td0、比例参数Kc0以及峰值时间tp.对198组试验数据进行分析拟合之后发现，对于确定的比例参数Kc0以及峰值时间tp，Td与Td0成线性比例关系：

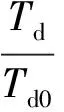
(10)

比值B的大小取决于Kc0与tp，但与模型参数量T1/T2的取值无关，B与Kc0、tp的关系式为：

(11)

2.4Ti的整定式

从式(3)可以看出：在不同的有效时间延迟θ取值情况下，积分时间参数的整定分为两种情况，根据Shamsuzzoha在文献[6]中所做的推导，得出：

(12)

Ti2=8θ

(13)

选取4个具有代表性的二阶时滞过程模型，与PD控制器组成闭环系统并进行设定值单位阶跃响应试验，对实验所得数据进行拟合处理(结果如同图7所示)，利用有效时间延迟θ与峰值时间tp的比值跟超调量之间的关系式，最终确定θ的取值.

图7 θ与tp的比值和超调量之间的关系

(1)对于具有较大时间延迟参数(T1/θ<8)的被控过程，θ与tp的比值介于0.16(T1/θ=8、超调量=0.1时)至0.49(T1/θ=0.1、超调量=0.6时)之间，在超调量的中间值0.3处，比值的变化为0.21～0.48.为了能得到较大的积分时间参数，可以保守地选择θ=0.49tp.因此，当具有较大的有效时间延迟常数时，积分时间参数的整定式为：

(14)

(2)对于具有较小时间延迟参数(T1/θ>8)的被控过程，θ与tp的比值介于0.14(T1/θ=100、超调量=0.1时)至0.26(T1/θ=0.8、超调量=0.6时)之间，选择平均值θ=0.2tp，而且在超调量中间值0.3处，比值的变化为0.19～0.21.因此，当具有较小的有效时间延迟常数θ时，积分时间参数的整定式为：

Ti2=1.6tp

(15)

3 仿真与对比分析

选取4个过程模型，分别用新整定法和SIMC法进行PID控制器参数整定，计算控制器与被控对象组成闭环系统的最大灵敏度Ms，并将其作为衡量控制系统鲁棒性的指标.Ms的计算公式为：

(16)

由于Ms等于在奈奎斯特曲线中从环路传递函数到临界点(-1，0)的最短距离值，因此，Ms值越小则说明控制系统的稳定裕量值越大，即鲁棒性越高.对比结果如表1所示.

以表1中第一个过程模型为例，以新整定方法和SIMC法所得结果构成的PID控制器与被控对象组成闭环系统，在t=0 s时进行单位阶跃响应，并在t=40 s时加入单位阶跃作为负载扰动，对比仿真结果如图8所示.

通过计算输出量的绝对误差积分(IAE)和输出量的总变分(TV)来衡量系统响应的输出和输入控制性能，绝对误差积分和总变分的计算公式分别为：

(17)

(18)

其中，在利用(18)式计算之前需要将输入信号离散化为数组的形式，即[u1,u2,u3,…,ui…].还应该注意的是，总变分(TV)也可表示为：

(19)

即输入量微分的绝对值的积分值，因此总变分值可以很好地衡量信号的平滑度.并计算相应的超调量和峰值，如表2所示.如同最大灵敏度一样，绝对误差积分(IAE)和输出量的总变分(TV)两者的数值越小，表示控制器的性能越优越；但对于一个已经达到平衡状态的控制器而言，为获得更小的绝对误差积分(IAE)，只能增加总变分(TV)和最大灵敏度(Ms)值，反之亦然.

图8 响应结果的仿真对比

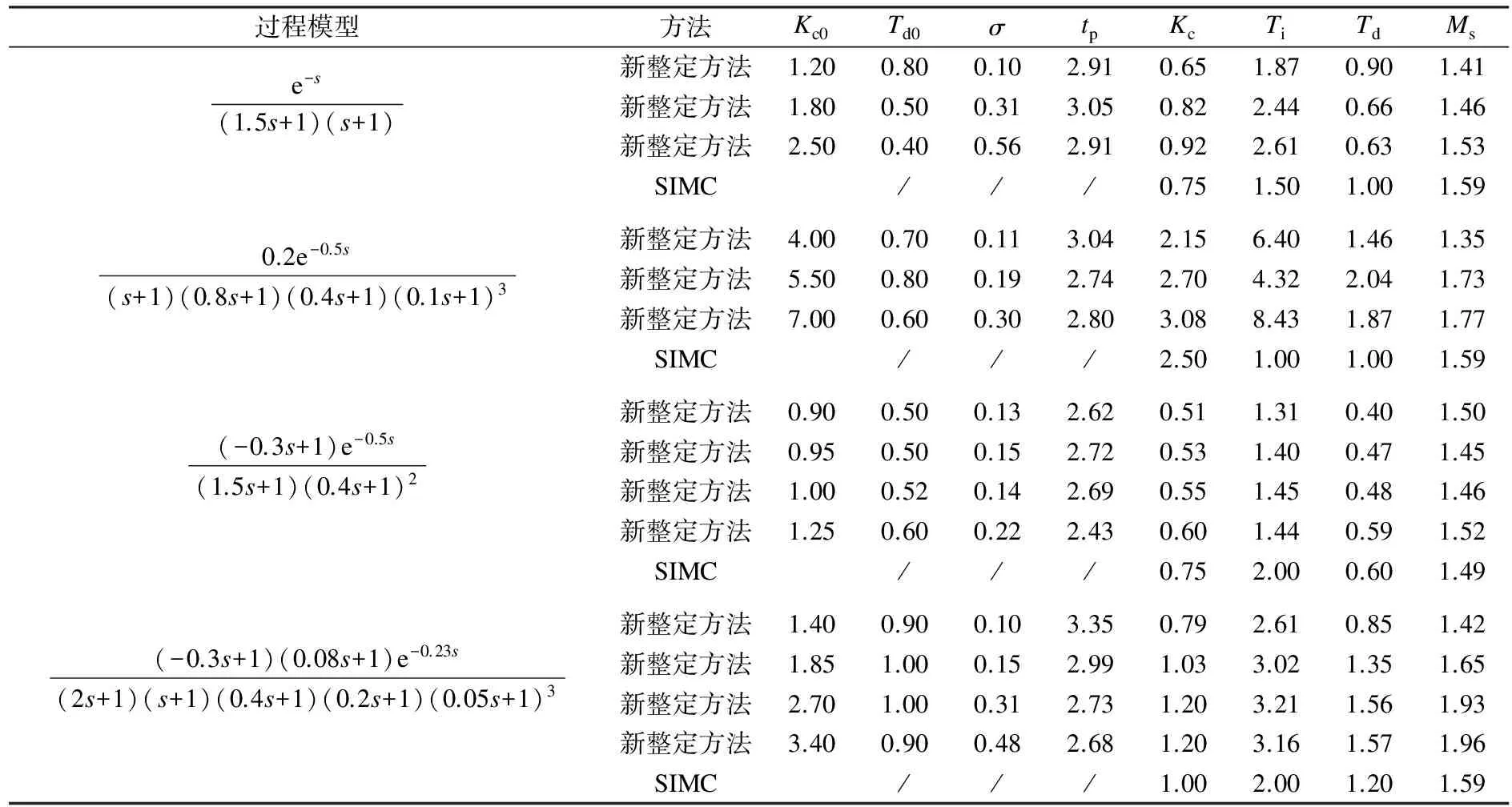
表1 新整定方法与SIMC(令τc=θ)的对比

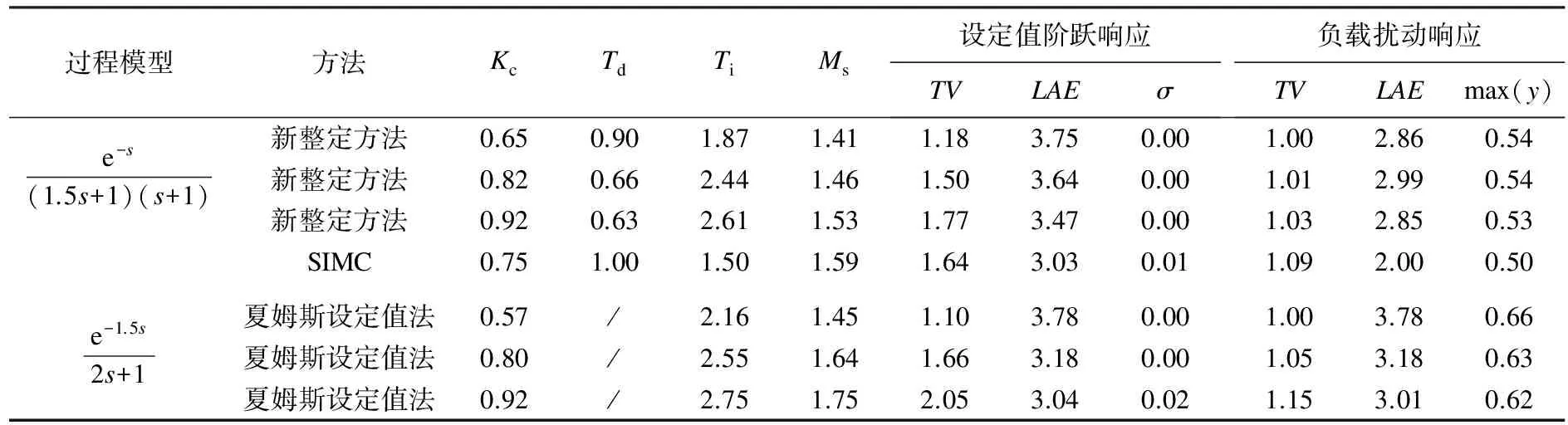
表2 响应性能指标的数据对比

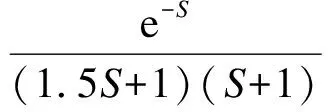
从表1和表2的对比结果可以看出：由新整定方法计算得出的最大灵敏度值、输出量总变分(TV)值普遍比SIMC所得对应数值要小，说明由新整定方法计算得出的控制系统鲁棒性更高、系统控制性能更优越.而在与一阶模型的“夏姆斯设定值法”对比中发现，新整定方法所得控制系统对扰动的抑制能力更强.

4 结 论

设计了一种新的PID控制器参数闭环整定方法，对于被控对象模型未知的控制过程，将被控对象与PD控制器组成闭环系统并进行一次设定值阶跃响应，利用响应所得数据，即可根据关系式得出PID控制器的3个参数值.比例系数的参数整定式为：

Kc=AKc0/F

a=2.933σ2-2.975σ+1.062

b=-3.59σ2+3.811σ-1.502

c=1.47σ2-1.592σ+1.144

微分时间常数Td的参数整定式：

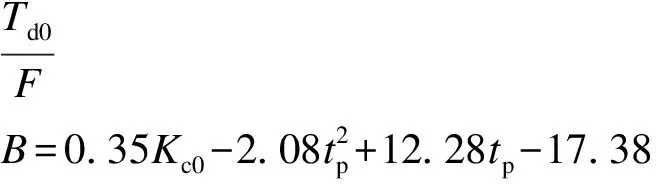
积分时间常数Ti的参数整定式为：

其中，F=1时，可得到较好的鲁棒性和适当的响应速度，两者处于一个平衡状态(对应于SIMC法中令闭环时间常数等于有效时间延迟)；如果想提高系统的鲁棒性，可适当增加F的取值，也可以通过减小F的取值来提高响应速度，但系统的鲁棒性会降低.与其它经典PID控制器参数整定方法相比，该闭环整定方法操作简单，且在控制系统的性能指标和鲁棒性方面也能取得理想效果.

[1] RIVERA D E，MORARL M，SKOGESTAD S.Internal Model Control.4.PID Controller Design[J].Ind.Eng.Chem.Process Dev，1986，25(1):252-265.

[2] SEBORG D E，EDGAR T F，MELLICHAMP D A.Process Dynamics and Control[M].New York:John Wiley & Sons，2004:134-208.

[3] SKOGESTAD S.Simple Analytic Rules for Model Reduction and PID Controller Tuning[J].Journal of Process Co-ntrol，2003，13(4):291-309.

[4] ZIEGLER J G，NICHOLS N B.Optimum Settings for Automatic Controllers[J].Transactions of the A.S.M.E.，1942，65(10):433-444.

[5] SKOGESTAD S，GRIMHOLT C.The SIMC Method for Smooth PID Controller Tuning[M].Berlin:Springer，2011:149-155.

[6] SHAMSUZZOHA M，SKOGESTAD S，HALVORSEN I J.A Simple Approach for On-line PI Controller Tuning Using Closed-loop Setpoint Resp-onses[J].Computer Aided Chemical Engineering，2010，28(4):619-624.

[7] 袁德成.过程控制工程[M].北京：机械工业出版社，2013:55-56.

A New Closed-loop Approach for PID Tuning

WANG Jian-long， YUAN De-cheng， WANG Gong-min

(Shenyang University of Chemical Technology， Shenyang 110142， China)

A simple and new method is proposed for the PID controller tuning for an unidentified system by using closed-loop responses.The proposed method requires only one step test in the closed-loop system in which the process is controlled by the PD controller.A series of data is obtained from closed-loop step response，contain the overshoot，the corresponding time to reach the peak，controller′s proportional gain and the controller′s derivative time.Based on a range of second-order with delay test processes，two simple analytical correlations can be derived for the proportional gain，integral time and derivative time as equations set respectively.The proposed method is compared with the SIMC tuning rule，and not only gives good robustness，but also possess fine performance.

PID controller; closed-loop response; SIMC; second-order with delay model

2014-11-04

王建龙(1988-)，男，山东潍坊人，硕士研究生在读，主要从事复杂工业工程的建模与控制研究.

袁德成(1960-)，男，内蒙古阿拉善人，教授，博士，主要从事化工过程建模、控制与优化的研究.

2095-2198(2017)01-0083-08

10.3969/j.issn.2095-2198.2017.01.015

TP13

A